
Lecture 4-1 Parametric Model Method Prof.N Rao
Lecture 4-1 Parametric Model Method Prof. N Rao
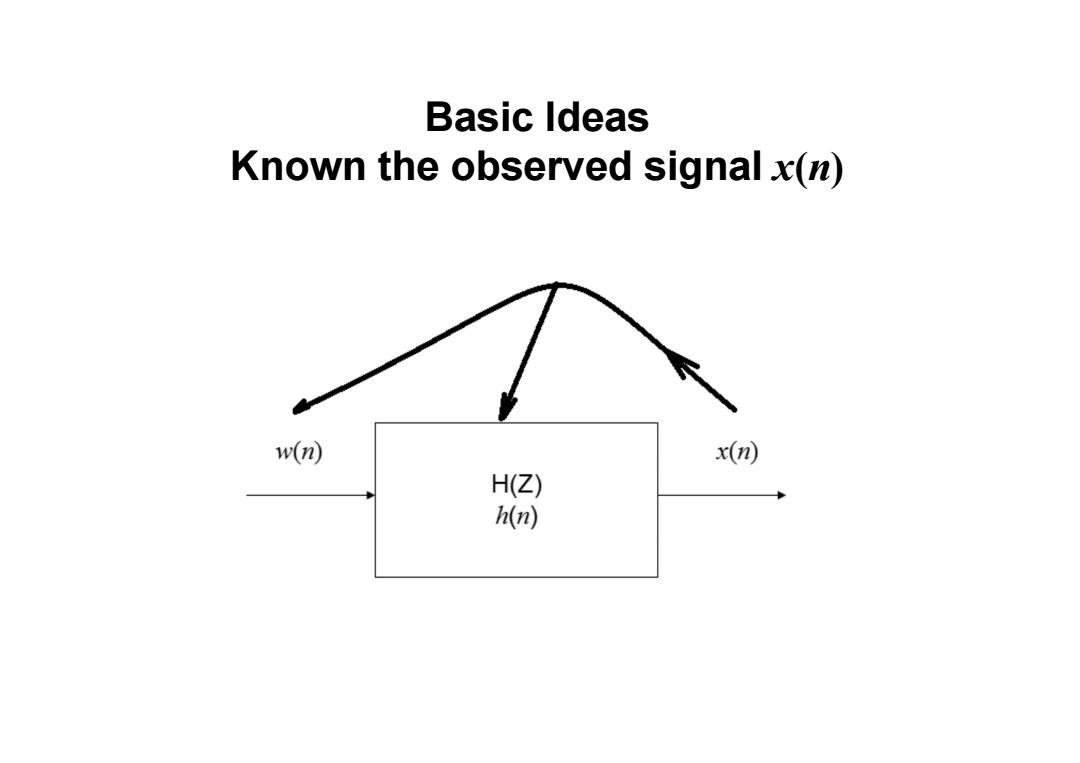
Basic Ideas Known the observed signal x(n) w(n) x(n) H(Z) h(n)
Basic Ideas Known the observed signal x(n)

Model transfering function:H(Z) 9 H2) X() w(n) x(n) W(z) H(Z) ) k=0 x(e吃a,:=w(e24: Assume a=1 dox(n)=-ax(n-k)+>b.w(n-k).do=I x(n)=-ax(n-k)+>bw(n-k).do=1
Model transfering function: H(Z) ( ) ( ) ( ) ( ) ( ) 0 0 0 0 0 0 0 1 0 ( ) ( ) ( ) 1 , 1 q k k k p k k k p q k k k k k k p q k k k k b z X z H z W z a z X z a z W z b z Assume a a x n a x n k b w n k a − = − = − − = = = = = = = = = − − + − = ∑ ∑ ∑ ∑ ∑ ∑

Three kinds of models x(n)=->dzx(n-k)+>bw(n-k).do=1 -0 1.Moving average (MA)model,denoted by MA(g). Except ao-1,all other ax=0,there are only zero points in H(. a=1 x(n)=∑b:w(n-k) () 得立
Three kinds of models 1. Moving average (MA) model, denoted by MA( q). Except a 0 =1, all other a k =0, there are only zero points in H( z). ( ) ( ) ( ) ( ) ( ) 0 0 0 1 q k k q k k k a x n b w n k X z H z b z W z = − = = = − = = ∑ ∑

Three kinds of models x(n)-->ax(n-k)+>bw(n-k).ao-1 k=0 (2)Autoregressive (AR)model,denoted by AR(p). Except bo=1,all other b-0,there are only pole points in H(. a0=1 x(n)=->ax(n-k)+w(n),b=1 H2) X()1 W(=)1+2a=
Three kinds of models (2) Autoregressive (AR) model, denoted by AR(p). Except b 0 =1, all other b k =0, there are only pole points in H( z). ( ) ( ) 0 0 1 1 1 ( ), 1 ( ) 1 ( ) ( ) 1 p k k p k k k a x n a x n k w n b X z H z W z a z = − = = = − − + = = = + ∑ ∑