
Three kinds of models x(m))=-2ax(n-k)+之bw(n-ka=l k=0 (3)Autoregressive moving average (ARMA) model,denoted by ARMA(p,q). Both ak and bk are not equal to zeros, h H2)= X( 、 k=0 W(z) k=0
Three kinds of models (3) Autoregressive moving average (ARMA) model, denoted by ARMA(p , q). Both a k and b k are not equal to zeros, 0 0 ( ) ( ) ( ) q k k k p k k k b z X z H z W z a z − = − = = = ∑ ∑
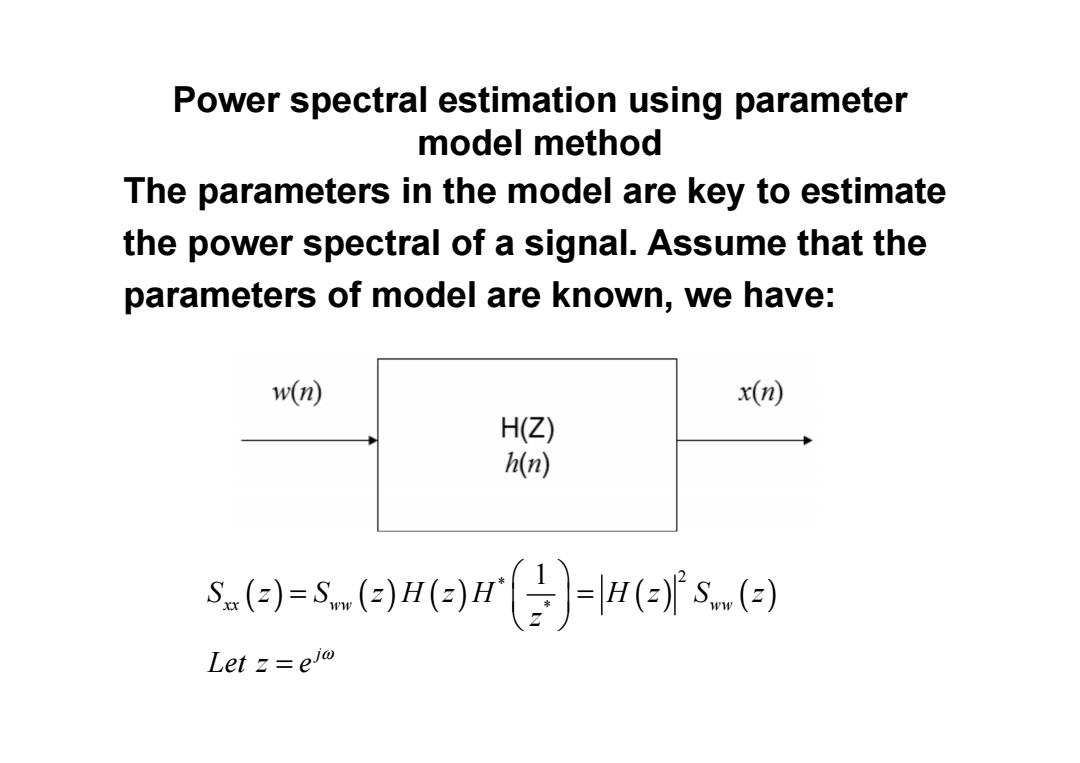
Power spectral estimation using parameter model method The parameters in the model are key to estimate the power spectral of a signal.Assume that the parameters of model are known,we have: w(n) x() H(Z) h(n) 5.()-5.(=)H()-H(=)s.(=) Let z=eio
Power spectral estimation using parameter model method The parameters in the model are key to estimate the power spectral of a signal. Assume that the parameters of model are known, we have: ( ) ( ) ( ) ( ) ( ) 2 * * 1 xx ww ww j S z S z H z H H z S z z Let z e ω = = =

Power spectral estimation based on MA model s.()=s()u()h=u(es(e) Let z=elo ao 1 x(n)=∑b4w(n-k) u(e)0昌三A:
Power spectral estimation based on MA model ( ) ( ) ( ) ( ) ( ) 2 * * 1 xx ww ww j S z S z H z H H z S z z Let z e ω = = = ( ) ( ) ( ) ( ) ( ) 0 0 0 1 q k k q k k k a x n b w n k X z H z b z W z = − = = = − = = ∑ ∑

Power spectral estimation based on AR model 5.()=s(e)Ha)H(日=(es(a Let z=eio ao =l x(n)=-∑ax(n-k)+w(n,b。=l H(a) X(2 2-1 w(日)1+2a
Power spectral estimation based on AR model ( ) ( ) ( ) ( ) ( ) 2 * * 1 xx ww ww j S z S z H z H H z S z z Let z e ω = = = ( ) ( ) 0 0 1 1 1 ( ), 1 ( ) 1 ( ) ( ) 1 p k k p k k k a x n a x n k w n b X z H z W z a z = − = = = − − + = = = + ∑ ∑

Power spectral estimation based on ARMA model 5.(=)=s..()H()H()s.(=) Let z=eio X(2) he* H(a)= k=0 W(z) k=0
Power spectral estimation based on ARMA model ( ) ( ) ( ) ( ) ( ) 2 * * 1 xx ww ww j S z S z H z H H z S z z Let z e ω = = = 0 0 ( ) ( ) ( ) q k k k p k k k b z X z H z W z a z − = − = = = ∑ ∑