
Lecture 5-2 Kalman Filter Applications Prof.N.Rao
Lecture 5-2 Kalman Filter Applications Prof. N.Rao
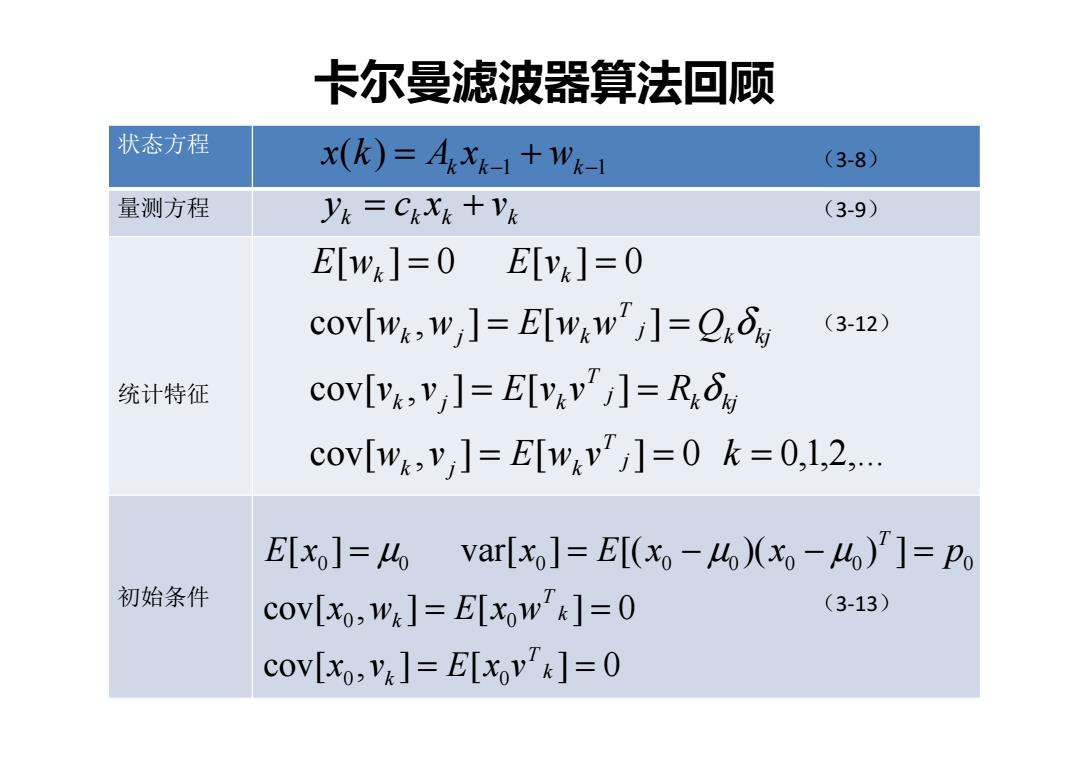
卡尔曼滤波器算法回顾 状态方程 x(k)=Akxk1+Wk-1 (3-8) 量测方程 yk=Ckxk +Vk (3-9) E[w]=0E[y]=0 COV[W&,W ]E[Wxw'j]=Qx8 (3-12) 统计特征 COVIV&:V ]ELVEv'j]=Rxo cov[w&,V ]E[wev']=0 k=0,1,2,... E[x]=4var[x]=E[(x,-4)(x-4)']=Po 初始条件 COV[Xo2 W&]=E[Xow]=0 (3-13) COV[xo,V&]=E[Xovk]=0
卡尔曼滤波器算法回顾 状态方程 量测方程 统计特征 初始条件 1 1 ( ) = k k − + wk − x k A x k k k k y = c x + v cov[ , ] [ ] 0 0,1,2,... cov[ , ] [ ] cov[ , ] [ ] [ ] 0 [ ] 0 = = = = = = = = = w v E w v k v v E v v R w w E w w Q E w E v j T k j k k kj j T k j k k kj j T k j k k k δ δ cov[ , ] [ ] 0 cov[ , ] [ ] 0 [ ] var[ ] [( )( ) ] 0 0 0 0 0 0 0 0 0 0 0 0 = = = = = = − − = k T k k T k T x v E x v x w E x w E x µ x E x µ x µ p (3-8 ) (3-9 ) (3-12 ) (3-13 )
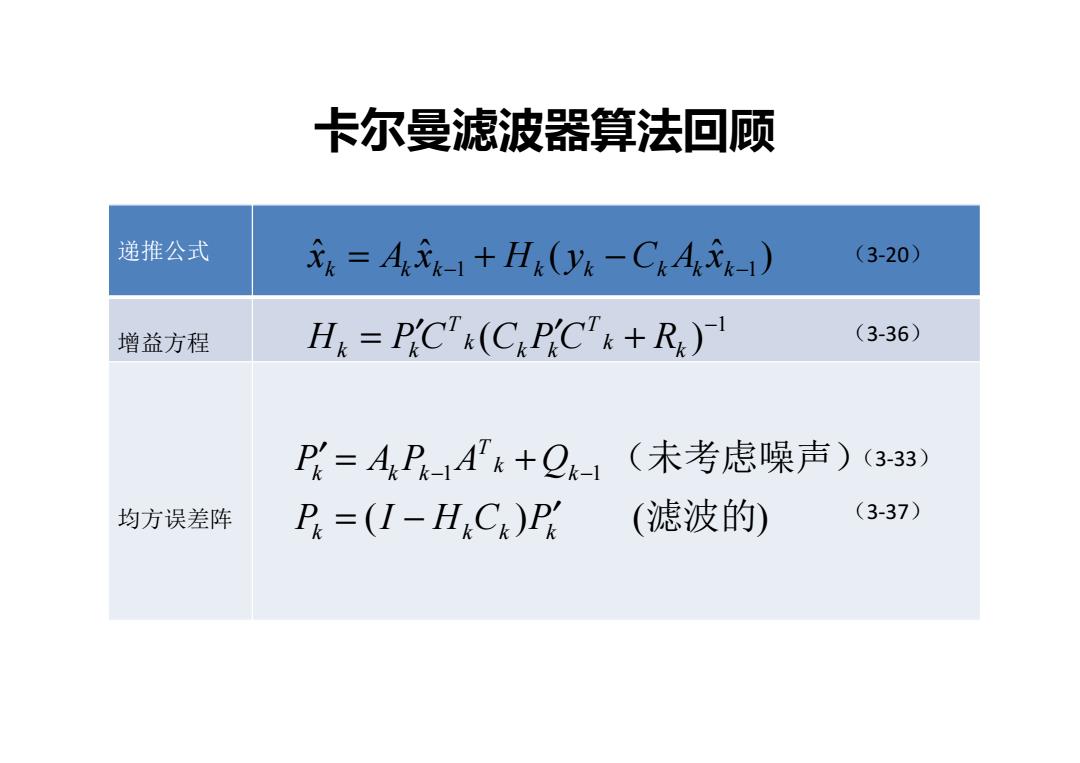
卡尔曼滤波器算法回顾 递推公式 元=Ax-1+H(0yk-CkA无k-) (3-20) 增益方程 H=P.CT&(CP.CTk+R) (3-36) P=A-1Ak+Q1(未考虑噪声)(3-3) 均方误差阵 P.=(I-HiCk)P (滤波的) (3-37)
卡尔曼滤波器算法回顾 递推公式 增益方程 均方误差阵 ˆ ˆ ( ˆ ) k = k k −1 + k k − k k k −1 x A x H y C A x 1 ( ) − = ′ ′ + k k T k k k T Hk Pk C C P C R ( ) ( ) 1 1 滤波的 (未考虑噪声 ) k k k k k k T k k k P I H C P P A P A Q = − ′ ′ = − + − (3-20 ) (3-36 ) (3-33 ) (3-37 )
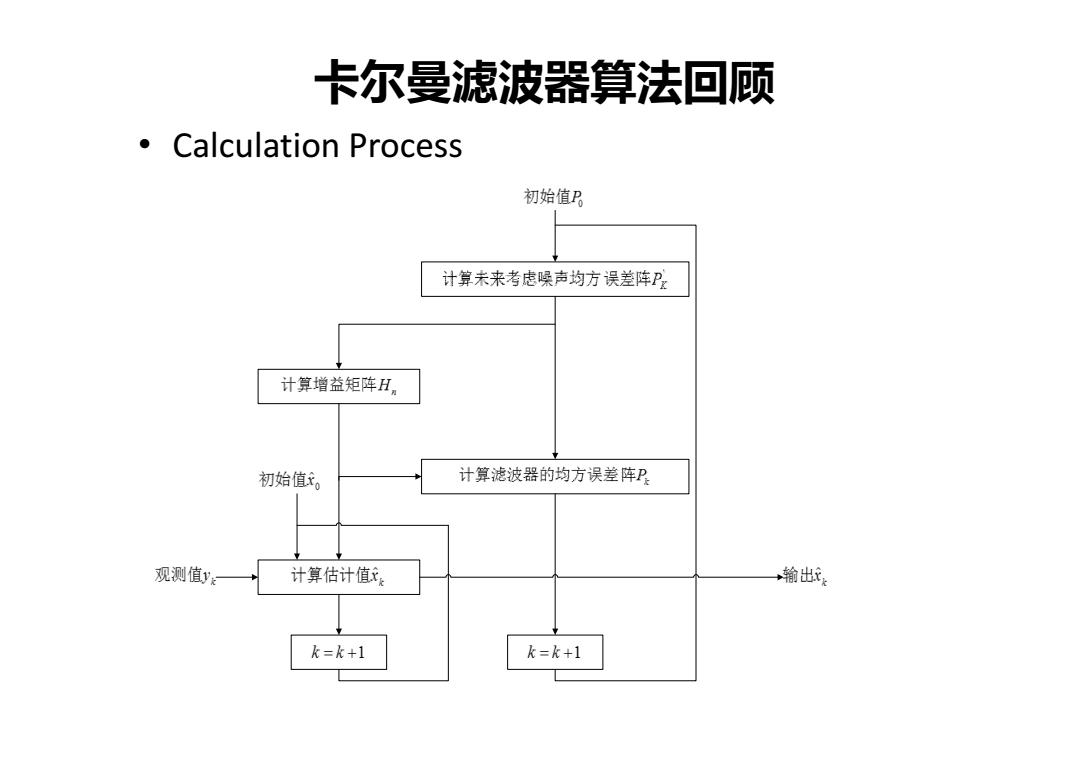
卡尔曼滤波器算法回顾 0 Calculation Process 初始值卫 计算未来考虑噪声均方误差阵P 计算增益矩阵H 初始值。 计算滤波器的均方误差阵P 观测值→ 计算估计值 +输出好 k=k+1 k=k+1
卡尔曼滤波器算法回顾 • Calculation Process

基于卡尔曼滤波理论的脑电逆问题反演 中国图像图形报,2009,14(5):838-842 引言 脑电系统的状态空间方程表达 ● 卡尔曼滤波法 实验结果及讨论 结论
基于卡尔曼滤波理论的脑电逆问题反演 中国图像图形报,2009,14(5):838-842 • 引言 • 脑电系统的状态空间方程表达 • 卡尔曼滤波法 • 实验结果及讨论 • 结论