中国地质大学（武汉）：《先进控制理论与控制工程》博士生课程教学资源（课件讲稿）第四讲 二维重复控制与主动扰动抑制

先进控制理论与控制工程 中国地质大学自动化学院吴敏 School of Aut 实例1一基于一维方法 设计问题： 对于给定的改进型重复控制系统，在系统鲁棒稳定的前提下，寻找低通滤波器的最大剪切频 率⊙。，使系统具有最高的稳态跟踪精度 控制对象： ,()=A,x(0+B,4(0 y0)=Cx,() 不确定性： Ap=Ap0+AA,(t),B。=Bp0+△B,(t) [AA,0△B,()]=Φ，r)[ΨAΨ] ΓT(t)r(t)≤I,t≥0 系统结构设计： 引入状态反馈控制增益K。,K。,提高系统鲁棒稳定性，改善系统暂态性能 113 2021年9月13日

113 2021年9月13日 设计问题： 对于给定的改进型重复控制系统，在系统鲁棒稳定的前提下，寻找低通滤波器的最大剪切频 率 wc ，使系统具有最高的稳态跟踪精度 控制对象： ( ) ( ) ( ) ( ) ( ) p p p p p p x t A x t B u t y t C x t         不确定性：   0 0 T ( ), ( ) ( ) ( ) ( ) ( ) ( ) 0 p p p p p p p p p A B A A A t B B B t A t B t t t t I t   D   D     D D           ， 系统结构设计： 引入状态反馈控制增益 K K e p , ，提高系统鲁棒稳定性，改善系统暂态性能 实例1—基于一维方法 先进控制理论与控制工程 吴 敏

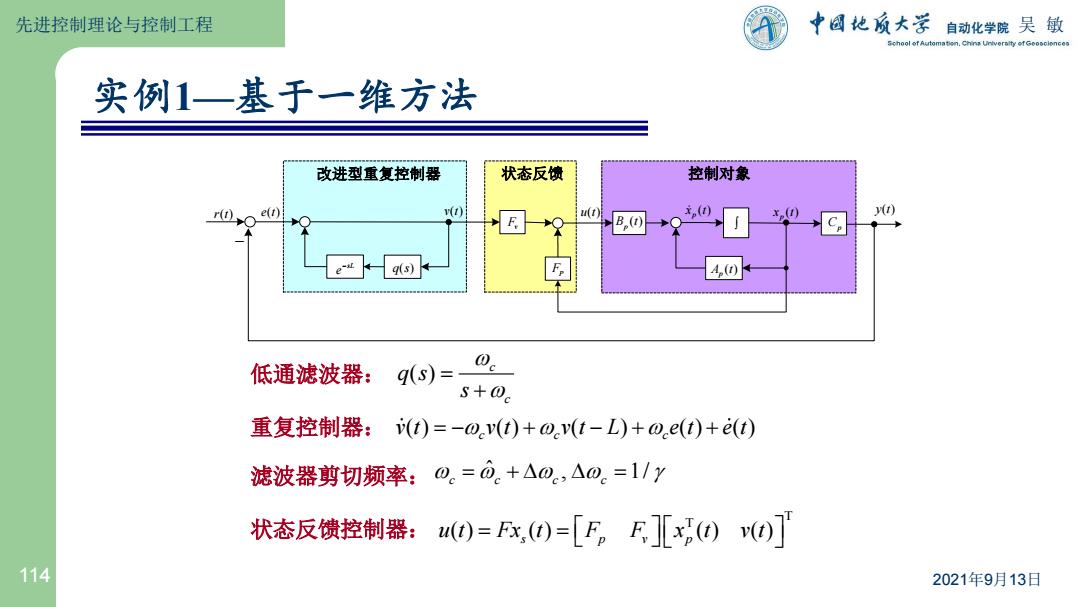
先进控制理论与控制工程 中国地质大学自动化学院吴敏 实例1一基于一维方法 改进型重复控制器 状态反馈 控制对象 (t) (t) ) e q(s) 4,0 低通滤波器： 9s)=_0 s+@c 重复控制器：(t)=-o.v(t)+o.v(t-L)+o,e(t)+E(t) 滤波器剪切频率：0。=0.+△0。，△0。=1/y 状态反馈控制器：)=x,)=[F。F][x0)v)] 114 2021年9月13日

114 2021年9月13日 ( ) ( ) ( ) ( ) ( ) c c c 重复控制器： v t v t v t L e t e t  -  -   w w w 状态反馈控制器： T T ( ) ( ) ( ) ( ) s p v p u t Fx t F F x t v t         ˆ , 1/ 滤波器剪切频率： w w w w  c c c c   D D  vt() sL e - F v () p rt() x t p () x t yt()  FP ut() Cp () A t p et() － 改进型重复控制器 控制对象 () B t p qs() 状态反馈 ( ) c c q s s w w   低通滤波器： 实例1—基于一维方法 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆记质大学自动化学院吴敏 School of Aut 实例1一基于一维方法 鲁棒稳定性定理1： 给定状态反馈控制增益F,如果存在对称正定矩阵P,Q,9,以及常数入>0， 使得如下 两个LMⅡ成立，则剪切频率为⊙。时系统鲁棒稳定 e<YCo (a) PAo+AP+Q+2ΨT平PAao PΦ PAcu Ac P-PAcld 0 -0 0 -AI 0 (b) 最大剪切频率®m设计问题：对于给定的F和剪切频率o。,求解如下广义特征值最小化问 题，从而获得最大剪切频率：om=o。+1/y min y>0s.t.LMIs (a),(b) 115 2021年9月13日

115 2021年9月13日 鲁棒稳定性定理1： 给定状态反馈控制增益 ，如果存在对称正定矩阵 ，以及常数 ，使得如下 两个LMI成立，则剪切频率为 时系统鲁棒稳定 0 1 F P Q Q , ,   0 wc Q Q 1 0   T T T cl0 cl0 0 cld0 cl1 cl1 1 cld1 0 1 0 0 0 0 PA A P Q PA P PA A P Q PA Q Q I               -      -  -    -       min 0 s.t. LMIs (a),(b)   (a) (b) 最大剪切频率 设计问题：对于给定的 和剪切频率 ，求解如下广义特征值最小化问 题，从而获得最大剪切频率： wcm c w ˆ cm c w w    ˆ 1/F 实例1—基于一维方法 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆记质大学自动化学院吴敏 School of Aut 实例1一基于一维方法 鲁棒稳定性定理2： 对于给定的O。,如果存在对称正定矩阵X和适合维数的矩阵W,使得如下LMⅡ成立 ⊙11 ⊙13 -1 0 <0 -1 其中 O1=AX+Bg2W+(AX+BW)） O3=(CX+DgW） 则系统鲁棒稳定，对应的状态反馈控制增益为：F=WX 116 2021年9月13日

116 2021年9月13日 11 1 13 0 0 B g I I        -          - 则系统鲁棒稳定，对应的状态反馈控制增益为： 1 F WX -      T 11 2 2 T 13 1 12 : : g g g g g g A X B W A X B W C X D W         其中 鲁棒稳定性定理2： 对于给定的 wc ，如果存在对称正定矩阵 X 和适合维数的矩阵 W ，使得如下LMI成立 实例1—基于一维方法 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆记质大学自动化学院吴敏 实例1一数值仿真 同时优化剪切频率和状态反馈控制增益的迭代算法： (流程图见论文Page7,Fig7 Flowchart of algorithm,略) 数值仿真： 控制对象参数： 「-1 A0\2 -c, 0 fro-t o sin0.lπt 0 cos0.1πt 1 0.1 世房 2π，.1.4π.1.6π 参考输入信号：r)=sin51+2sint+2n5 t 117 2021年9月13日

117 2021年9月13日 同时优化剪切频率和状态反馈控制增益的迭代算法： （流程图见论文Page 7, Fig 7 Flowchart of algorithm，略 ) 数值仿真： 控制对象参数： 0 0   1 3 1 , , 1 0 2 3 0 0 0 sin 0.1 0 , ( ) 1 0.1 0 cos0.1 1 0 0.1 , 0 0.1 0 p p p p A B A B C t t t        -             -                                       参考输入信号:   2 1 4 1 6 sin sin sin 5 2 5 2 5 r t t t t        实例1—数值仿真 先进控制理论与控制工程 吴 敏