
(M)=in=火x(u)-gx(2=9业6(u-sin2 (1.39) 8 12 sinu 24 sinu 4 方程右边的这三角函数,可以4代替中()表达式中的2“而用附 录的表A-1进行計算. 当作用于两端固定的梁-柱上的横向荷重不对称时,两端的弯 矩可由两端的斜率为零的条件得出,因此,对于图1.12所示的梁, 决定两端点弯矩M。与M。的方程为 0。=6。+M()+M(w)=0, 3ET 6EI (1.40) 0。=0b+M,(n)+M2p()=0. 6EI 3EI 在这两个方程中,0与6表示当Q单独作用时铰支梁两端的簪 角”,它們可由方程(1.9)与(1.10)得到. M c-H M B形P y 图1.12 51.9.有弹性約束的梁-柱 作为一个更为一般的靜不定間题,我們来研究一两端弹性固 定的杆.这种端点状况的实例如图1.13a所示。一承受横向荷重 的梁AB,于A,B处刚性地固結于两铅直杆,并承受軸向压力P, 若0。与0。为两端的轉角,則在梁的两端将产生两力偶M。与M6 (图1.13b),它們可表示为如下形式: M。=-cd。,Mb=一B0b. (1.41) 图1.13示出了正的弯矩与轉角.因子a,B为规定杆端固定程度 的系数,称为端点韵束系数.当杆端的轉角等于1时,此系数在数 1)取图1.8a所示的转衡与臂矩M,及Mb为正。 ·180
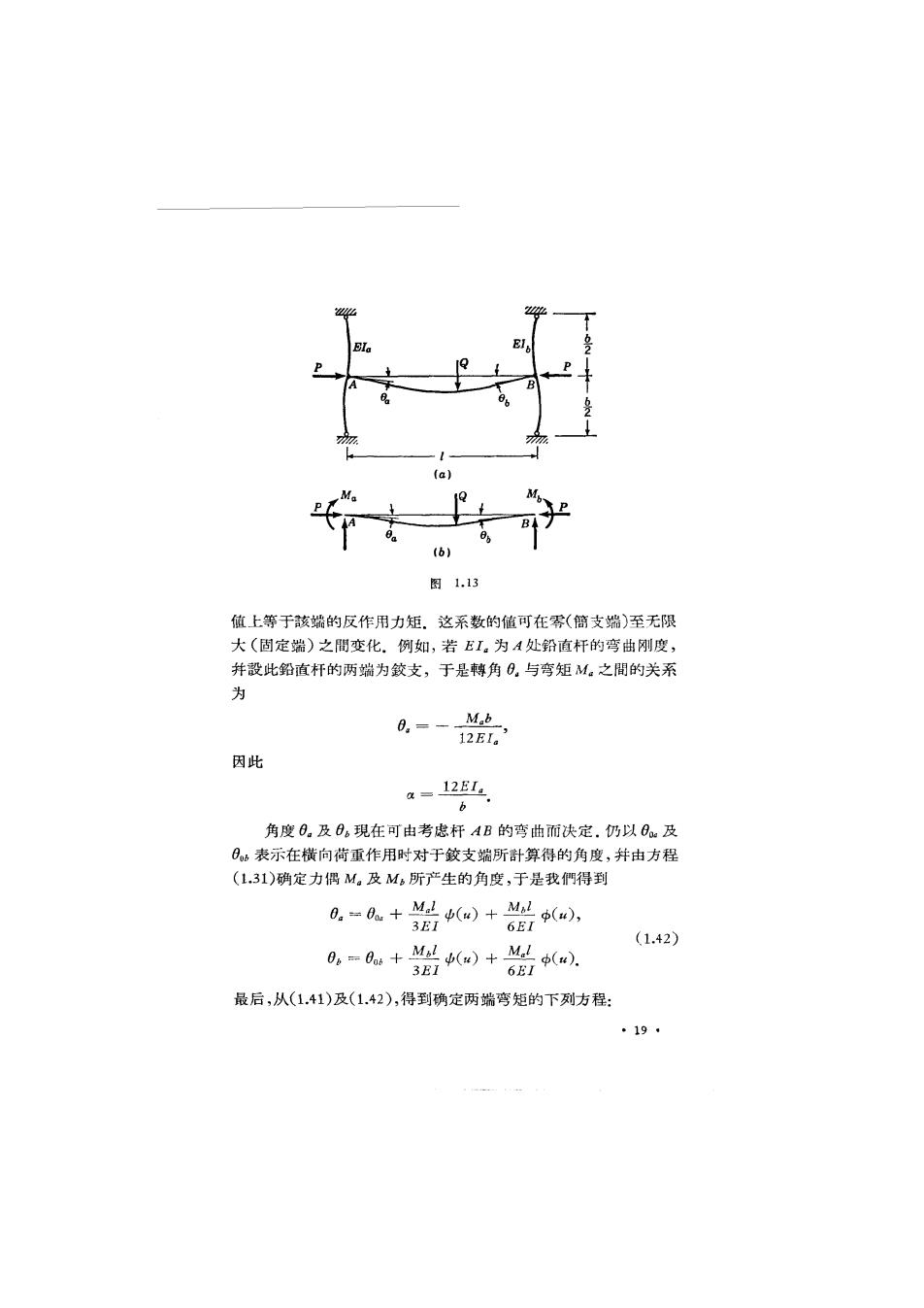
P (a) b 图1.13 值上等于該端的反作用力矩.这系数的值可在雾(簡支端)至无限 大(固定端)之間变化.例如,若EI。为A处铅直杆的弯曲刚度, 并設此铅直杆的两端为鉸支,于是轉角0。与弯矩M。之間的关系 为 0。=-Mab 12EL。3 因此 a=12EIs b 角度0。及日。現在可由考虑杆AB的弯曲而决定.仍以0及 表示在横向荷重作用时对于鉸支端所計算得的角度,并由方程 (1.31)确定力偶M。及M6所产生的角度,于是我們得到 0。=a+M.(a)+4Lp(w, 3EI 6EI (1.42) 0。=0as+Mb(m)+M 3EI 6EI (4). 最后,从(1.41)及(1.42),得到确定两端弯矩的下列方程: ·19·

-M=+42()+Ma(w), 3EI 6EI (1.43) -4=6+N(w)+M(). B 3EI 6EI 用了这些方程,可以研究杆AB的各种端点状况.例如,取 a=0,B=o,我們得到图1.10所示的情况,即杆的左端可自由 轉动而右端为固定端。在这种情况下,M。一0,而B端的弯矩为 [方程(1.43)的第二式] M.=-3EI0o (a) 中() 若杆AB系承受均布荷重,則由方程(1.22)得 0b=9X(). (b) 24EI 将式(b)代入式(a),得固定端的弯矩,其精果与以前所得的相同 [参閱方程(1.37)]. 取α=B=∞,我們得到两端固定的杆这情形,并且方程 (1.43)化为前节的方程(1.40).方程(1.43)的应用将在以后討論 稳定性間题时給出(参閱52.3). 51.10.有轴向荷重的連精梁 刚性支座上的速續梁对于-一承受横向及軸向荷重共同作 用,并由刚性支座所支承的連较梁,以位于支座上方截面内的弯 矩作为静不定量是得当的.分1,2,·,m表示相雜的支座,M1, M2,·,Mm为相应的弯矩,1,2,·,1m-1为跨度,,,·, m-1为各跨度相应的4值[由方程(1.13)】.压力与弯曲刚度对于 各跨度可以各不相同,但在各跨度内这些量均設为常数. 我們来研究支座n一1,n及”十1間的两个相邻的跨度(图 1.14).支座上方截面内的正的弯矩如图所示,它們使梁的頂部受 压;与正弯矩方向相同的牌角为正」 相应的弯矩Mm-4,Mn,M。+1之間的关系,可由这两个跨度的 挠度曲犧在中間支座上有一公切椴这条件而得到.跨度n一1右 端的轉角日。与跨度n左端的轉角,必大小相等,但正负号相反, ·20·

Ma+l n+1 图1.14 因此 0.=-8n. (a) 以每一跨度作为承受横向荷重与端弯矩的簡支梁,以計算轉 角。故轉角0。的表达式包括两部分,其一与作用于这跨度的横向 荷重有关,以m表之;第二部分与力偶Mn-1及Mm有关,并可得 自方程(1.31).如是 0。=on+4=(4)+M(-. 6EI-1 3EI#1 对于角8,我們也可以写出同样的表达式.于是方程(a)成为 ++会 6EI-1 =-6.+此以)+, 3EIn 6EI 由此 )+2业.)+是2o+ +M么会)=6影a+.1) n1 对于任何种横向荷重,角0.及%.可用551.3至1.5藷节所述的 方法来計算.所以方程(1.44)只有三个未知的弯矩Mm-1,Mn: M+1.对于速镀梁的每一中間支座写出方程(1.44),并运用第一个 及最后一个支座处的条件,我們就得到足够的方程去解所有的未 知力矩,方程(1.44)为有軸向荷重的速貔梁的三弯矩方程, 若強度为q-1及qm的均布荷重各作用于跨度n一1及n,則 由方程(1.22),我們得到 6o.=9a-X(-, Γ24EIn-1 ·21

6n=4X(,), 24EI. 而方程(1.44)可写成如下形式: M(-)+2M.[u-)+1()+ In-1 In 人1(w)=-4-X(w)- Mat I. 4 gt 1n 1 x(ua). (1.45) 4 In In-1 用了附录的表A-1中函数中(),()及X(4)的值,用上远方程 来計算弯矩将大大簡化. 支座不位于,直线上的连续梁若一原来直的压杆为不位于一直线上 的刚性支座所支承,则将产生附加的弯曲。设n一1,n及n十1为连续粱的 三个相继的支座(图1.15),h-1,n及hn+1为各支座相应的积坐标,我们 Mn-1 P- 图1.15 假设这些坐标相差非常小,以致两相邻跨度间的夹角βm可足够精确地由下 列方程表出: 月n=。-Al-+1一A (b) 【n-1 由于支座位橙的高度差所引起的弯矩Mm-1,M。及Mn+1,可由连续条件得 到。若以跨度为一1及n作为两个简单梁,我们得到结论:在公共支座严 上,这两梁的两端所转的角度必须与角度B。相抵消.于是运用方程(1,31), 我们得到 a=(-)+MaaL(wn-)+(n)+ 3EIn-t 6EIn-1 +Mn+山中(n)=Ba, ·22