
代换以及方程(1.13),可证明这结果与方程(1.20)相同. 51.6.由力偶引起的梁-柱的弯曲 有了单个集中荷重9作用(图1.3)的解,就不难得到一力偶作 用于梁端时的挠度曲钱方程.为了求这方程,殷图13中的距离 c趋于客,而同时Q則在增大,务使乘积Qc为一有限值且等于 M.在趋于极限时,我們就得到在力偶M。(图1.7)作用下杆的弯 曲.由方程(1.7),代入sinc=c,Qc=M,即得挠度曲钱 y=M(sin kx-¥) (1.24) 图1.7 在我们以后的讨论中,有必要知道在杆两端的微小轉角0。,0。 的公式.当杆端的轉角是按照正的弯矩方向而轉时,这轉角为正, 图1.7.计算式(1.24)的导数,得到 0。=(y)=M(饣- ,=pm:=) =ML3(1- 1 (1.25) 6E14\sin242w/ 06-- dy 、dx/x= Psin kl =ML3(1-1 (1.26) 3EI 2u2u tan 2u/ 可以看出,力偶M。单独作用时所产生的轉角M6l/6E1及 M6/3E1,乘上了一三角函数因子,表示出軸向力P对于杆两端轉 角的影响.不难証明,当4趋近于零时,以上这两因子趋近于1; 当“趋近于x/2时,这两因子将无限地增大.在以后的方程中,将 ·13
用以下的記号以筋化表达式: (w)=3 1-一 (1.27) sin 2t (4)= 1) (1.28) 这两个函数的数值可查附录的表A-1. 若有两个力偶Ma,M6分别作用于杆的A,B两端(图1.8a), M M B\P (a) B -x (b) 图1.8 挠度曲辍可由迭加而得.从方程(1.24),得到力偶M6所产生的挠 度.在这方程中,以Ma代替M6,(1一x)代替x,便得到力偶M.所 产生的挠度.将这些秸果相加,得图1.8α所示的梁的挠度曲钱为 y=学(儡餐-》+学[血, PL sin kl ,(1.29) 当两个佩心压力P作用时,图1.8b,我們就有这样的荷重.将 M。=e.P,M6=e6P代入方程(1.29),得到 y=(儡转-》+恤-片 .(1.30) 运用方程(1.25),(1.26)及記号(1.27),(1.28),即可得到图 1.8a中杆两端的轉角0。及0。.于是由迭加, 0。=(w)+4(, 3EI 6EI (1.31) 0。=M()+Mg(. 3EI 6ET ·14

运用附录中表A-1的中()及()的值,即可很容易地自方 程(1.31)得到角度0。及0. 当两力偶相等,即M。=M6=M时,自方程(1.29)得到 l(告-创-m劉 y=Mo 2 -am(-9)-w小 (1.32) 代入x=1/2,杆中点的挠度为 0=(yn=g21-cos0=M,x(.(1.3) 8EI 8EI 由式(1.32)的导数并代入x=0,邮得杆两端的轉角.秸果为 8=--(经)-治巴 (1.34) 发生于杆中点的最大弯矩,可由式(1.32)的二阶导数得到, Mar=-Er(y) (1.35) dx2)tin =Mo sec # 式(1,35)可用以計算杆承受两隔心压力且偏心距相等时的最 大弯矩(图1.8b).当軸向力P比临界值[方程(1.15)]小得多时, “的数值就很小,scw可取作等于1,卸可假設弯矩沿杆长为一常 数.当4趋近于元/2,即P趋近于Pcr,sec4将无限地增大.对Pcr 附近的P值,荷重作用点的稍微偏心会在杆的中点产生相当大的 弯矩.对于这种情形的資用应力,将在§113内討論。 §1.7.挠度的近似公式 在作初步的殷計計算时,如果有一近似公式来决定筋支端梁一 柱中点挠度,常常是有用处的.在前几节中,會对三种对称荷重 (中点处的集中力,均布荷重,及两个相等的端弯矩)得到了中点挠 度的表达式.对于每一情形,挠度等于两项的乘积,第一項为无軸 向力时的挠度,第二项为依赖于4值,从而依赖于比值P/Pc[参 閱式(1.16)]的放大因数.对于这三种荷重情形的放大因数各为 X(4),7()及λ(4). ·15·
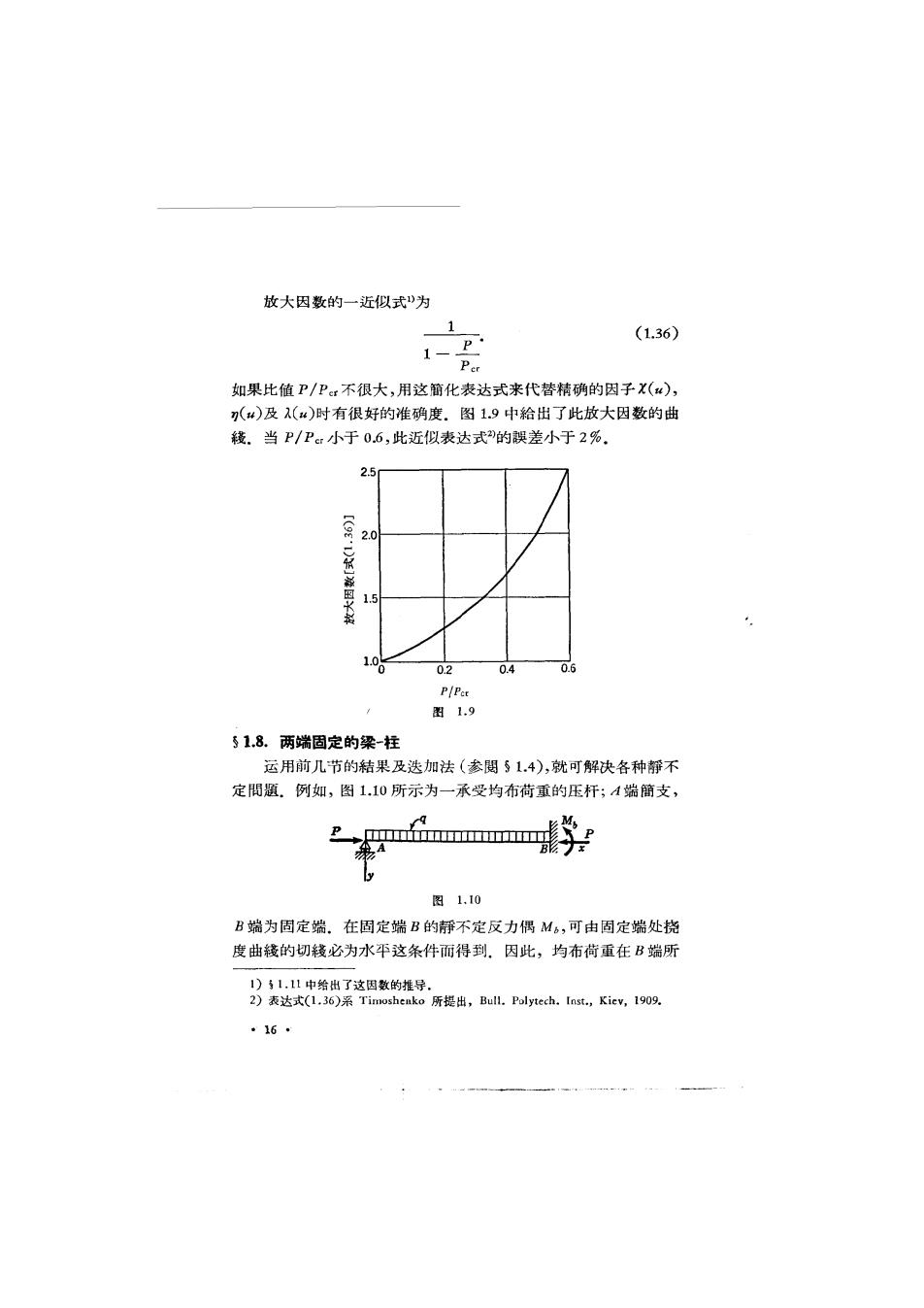
放大因数的一近似式》为 1 I、P (1.36) Per 如果比值P/P:不很大,用这簡化表达式来代替精确的因子X(), (4)及(4)时有很好的准确度.图19中給出了此放大因数的曲 辍.当P/Pc小于0.6,此近似表达式的誤差小于2%. 25 20 国 1.5 1.0 0 0.2 0.4 0.6 P(Pet 图1.9 51.8.两端固定的梁-柱 运用前几节的结果及迭加法(参閱§1.4),就可解决各种静不 定間题.例如,图1.10所示为一承受均布荷重的压杆;A端簡支, M IIII形 A B ly 图1.10 B端为固定端.在固定端B的静不定反力偶M6,可由固定端处挠 度曲辍的切钱必为水平这条件而得到.因此,均布荷重在B端所 1)青1.11中给出了这因数的推导. 2)表达式(l.36)系Timoshenko所提出,Bull.Polytech.【nst.,Kiev,1909. ·16

产生的轉角[方程(1.22)],与力偶M6所产生的轉角[方程(1.31) 第二式]之和必等于零.这样,得到 gx()+M()-0, 24EI 3EI 由此 M。=-9.X(2 (1.37) 8() 負号表示M6的方向与图1.10中所設的相反,使梁向上凸起而弯 曲.弯矩M6可由附录的表A-1很容易地算得.有了弯矩(1.37), 挠度曲犧可由均布荷重所产生的挠度[方程(1.20)]和弯矩M6所 产生的挠度[方程(1.24)]迭加而得. 若受均布荷重梁的两端均为固定(图1.11),則挠度曲镂为对 称,并且固定端的弯矩相等(M。=M6一M).这两弯矩的大小可 由这一条件得到,即均布荷重所产生的两端的轉角[方程(1.22)], 被作用于两端的弯矩所抵消[方程(1.34)].于是 qx()+Mil tanu0, 24EI 2EI 4 由此 M。=-gX() (1.38) 12 tanu 負号依然表示弯矩的方向与图1.11所没的相反.有了这端弯矩, M。 9 M P iTCk AA B形 y 图1.11 挠度曲後可由均布荷重所产生的挠度[方程(120)]和作用于两端 的两相等力偶所产生的挠度[方程(1.32)]迭加而得.同样,中点 的弯矩可由均布荷重所产生的弯矩[方程(1.23)】与两力偶M,所 产生的弯矩[参閱方程(1.35)与(138)]迭加而得,郎 .17