
若略去剪切变形及梁軸钱縮短的影响,則梁軸後的曲率的表 达式为 EI=-M, dx2 (1.3) EI为梁在弯曲平面内的,即在所殼的对称面xy平面内的弯曲刚 度.将方程(1.3)与方程(1.1),(1.2)粗合,可将梁軸钱的微分方程 表成别种形式: EI y+p dy=-v, (1.4) dx3 dx 及 B1兴+P兴=4. (1.5) dx dx? 方程(1.1)至(1.5)为梁-柱弯曲的基本微分方程.若軸向力P为 零,这些方程都化为只由横向荷重所弯曲的方程. 我们可以截取一垂直于梁挠曲轴线的做段(图1,2c),而不用侧面垂直 于x轴的微段dx(图1.2b).由于粱的斜率是小量,垂直于微段侧面的力可 取为等于轴向压力P.对于这情形,剪力N与图1.2b的剪力V之间由表达 式 N=v+pdy (a) 相联采;于是代替方程(1.1)与(1.2),得到 9-+ dx? (1.1a) 和 N=dM dx· (1.2a) 方程(1.1a)与(1.2a)亦可由图(1.2c)中微段的平衡获得.最后,将方程 (1.2a)与方程(1.3)组合,得 和祭=-议 (1.4a) 方程(1.5)对于图(1.2)中的微段亦适用,于是,按照在垂直于粱已挠曲或 未挠曲的轴线上来取购力,对于粱-柱有两组微分方程. ·3·
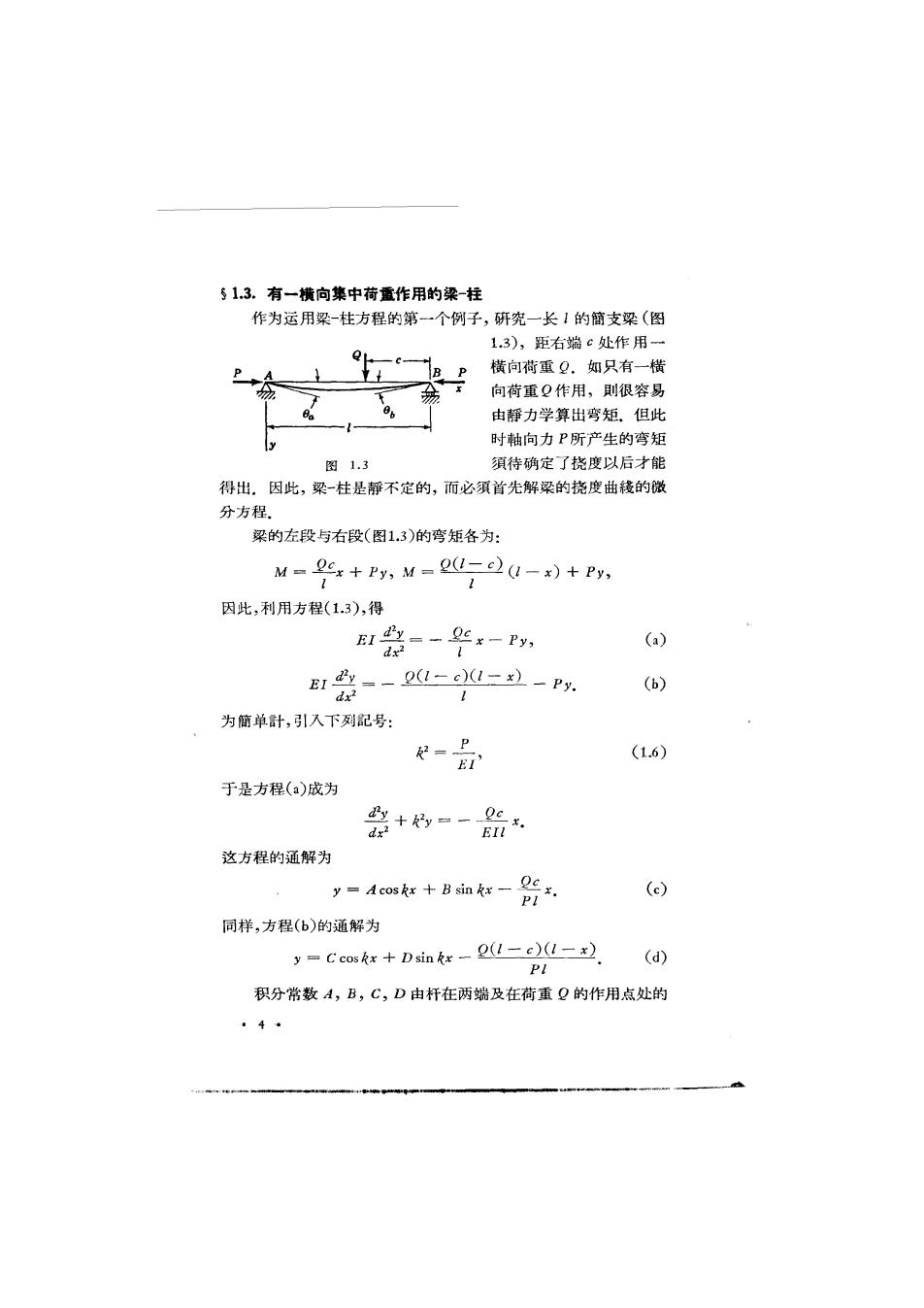
513.有一横向集中荷重作用的梁-柱 作为运用梁-柱方程的第一个例子,研究一长!的簡支梁(图 1.3),距右端c处作用一 B P 横向荷重9.如只有一横 向荷重作用,則很容易 由静力学算出弯矩.但此 y 时軸向力P所产生的弯矩 图1.3 須待确定了挠度以后才能 得出。因此,梁一柱是靜不定的,而必須首先解梁的挠度曲钱的微 分方程. 梁的左段与右段(图1.3)的弯矩各为: M-ex+Py:M-(1)(4-x)+Py, 因此,利用方程(13),得 EI=-华x-Py, (a) dx2 Er=-1-c)1-)-P (b) dx2 为簡单計,引入下列記号: 2=P r (1.6) 于是方程(a)成为 路+=-% d 这方程的通解为 y-Acoskx +B sin kx-e. (c) PI 同样,方程(b)的通解为 y=Ccoskx +Dsin kx-2(1-c)(1-x (d) 积分常数A,B,C,D由杆在两端及在荷重?的作用点处的 。4

条件来决定。由于杆两端的挠度为零,我們断定: A=0,C=一Dtan kl. (e) 在荷重Q的作用点处,由方程(c)与(d)給出的两段挠度曲後将有 相同的挠度及公切钱.于是 B sin k(I-c)-0e (1-c)=DI sin k(1-c)- Pl tanklcosk(1-c)1-Oe(1-c), PL Bkcosk(1-c)-Oc Dklcos k(1-c)+ Pl +tansin-c)】+-c2, 由上两式得 B=Osin ke D=-2sink(I-c) (f) PRsin kl PRtank! 将由(c),(f)所得的常数代入(c)与(d),我們得到挠度曲辍的两部 分的方程为: 0 sin ke sin-,0≤x≤-c;(1.) y= Pksin kl y=sin1-2in1-x)-1-c-2, Pksin kl PL (l-c)≤x≤ (1.8) 我們可以看出,若以(1一c)代c,以(1一x)代x,則方程(1.8)可自 方程(1.7)得到. 計算(1.7),(1.8)两式的导数,得到在以后計算中有用的下列 諾公式: 、g=2 sin RC.coskx,0≤x≤(1-c); (1.9) dx Psin ki =-)sin-c)cos1-x)+2=c2 dx P sin kl (1-c)≤x≤1;(1.10) ,5·

0≤x≤(1一c);(1.11) dx2 P sin kl y=- d oksink(I-c)sin k(I-x), P sin Rl (1-c)≤x≤1.(1.12) 对于荷重作用于中点这特殊情况,挠度曲钱是对称的,于是只 須考虑荷重左边的这段.要得到在这特殊情况下的最大挠度,我 們将x=c=1/2代入式(1.7),得到 8-60n=0(an9- 2 (g) 2PR 为了笛化此方程,运用以下配号: RI 1P (1.13) 4=2=2VEI' 于是方程(g)成为 8=23tan-2=22x(w). (1.14) 48EI 48EI 这方程右边的第一个因子表示只有横向荷重作用时的挠度,第二 个因子X(4)表明了軸向力P对于挠度8的影响.在附录的表A-1 中給出了对于不同值的X(“)的数值.用了这表,就可由方程 (1.14)很容易地算出每一特定情形下杆的挠度. 当P很小时,4的数值也很小[参閱方程(1.13)],而因子X() 接近于1.这可用下列級数并只保留其为首的两项而証明之: tanw=私十号+2丝+… 3 3.5 还可以看出,当4趋近于元/2时,X()趋于无限大.当4=π/2 时,自式(1.13)得到 P=EI 2 (1.15) 这样,可得到桔論:当轴向压力趋近于方程(1.15)所給出的极限值 时,即使极小的横向荷重,也会产生相当大的挠度.这压力的极限 值称为临界荷重,并以P表示。运用了軸向力的临界值[方程 ·6…

(1.15)],4的值[参閱方程(1.13)]可表示如下: 7P (1.16) 4=2VP 这样,4只取决于P/Pc的值. 要計算梁的挠度曲後一端的斜牵,我們以c=/2,x=0代 入方程(1.19),于是, y =/1 11 =2(1-cos 2P cos 16EI cosu 2 =25(w). (1.17) 16EI 依然,第一个因子为横向荷重?单独作用于梁中点时所产生的斜 率,而第二个因子表示軸向力P的影响.附录的表A-2中給出了 因子(w)的值 运用方程(1.11),得到最大弯矩如下: Mmax=-EI() =EI2Ban延-=2an“.(1.18) dx2x=/2 2P 24 对于这情形,最大弯矩等于横向荷重所产生的弯矩乘以因子 tan/4.当轴向压力逐漸变小时,这因子以及以前的三角函数因 子λ()与X()的值趋近于1;而当量“趋近于x/2时,卸当压力 接近于临界值(1.15)时,这因子将无限地增大。 51.4.几个集中荷重 前一节的秸果可用于更一般的情形,即有多个横向荷重及軸 向压力共同作用于梁的情形.方程(1.7)和(1.8)指出,对于任一給 定的釉向力,杆的挠度与横向荷重Q成正比;同时,挠度与触向力 P之間的关系較为复杂,因这軸向力是包括在含有?的三角函数 内的。挠度为Q的钱性函数这事实表明:通常用于当梁只有横向 荷重作用时的迭加原理,箱加修改后亦能应用于横向荷重及轴向 力共同作用下的情形.从方程(1.7),(1.8)可以看出,当使横向荷 重9增加一量Q1,如作用于杆的軸向力相同,则总的挠度可自2 ·7