
5.7.在压力与端弯矩作用下的扭转屈曲261 第六章梁的横向屈曲… 6.1.横向屈曲的微分方程 ..269 56.2.纯弯曲梁的横向屈曲 271 56.3.悬臂梁的横向屈曲 275 6.4.简支工字梁的横向屈曲 6.5.简支狭长矩形截面梁的向屈曲286 56.6.横向屈曲的其他情形…… ..288 $6.7.工字梁的非弹性向屈曲…290 第七章圓环、曲杆与拱的屈曲 297 7.1.圆形细曲杆的弯曲…………… 7.2.应用三角级数分析薄圆环的弯曲 7.3.均匀压力对圆环弯曲的影响………… 306 7.4.在均布外压下圆环及管的屈曲308 $7.5.以所设的缺陷为根据设计受均布外压作用的管子…………313 7.6.均匀受压圆拱的屈曲 $7.7.其他形式的…322 $7.8.很扁平的曲杆的屈曲325 $7.9.两种金属组合小条的屈曲330 7.10.圆形轴线曲杆的横向屈曲.333 第八章薄板的弯曲…………………339 $8.1.板的纯弯曲…339 $8.2.在分布横向荷重作用下板的弯曲346 8.3.板受弯曲与拉伸或压缩的联合作用353 8.4.板弯曲的应变能355 $8.5.简支边矩形板的挠度361 8.6.具有微小初弯曲的板的弯曲…364 8.7.板的大度 366 第九章薄板的屈曲………369 9.1.临界荷重的计算方法.369 9.2.在一个方向均匀受压的简支短形板的屈曲372 9.3.在两垂直方向受压的简支矩形板的屈曲377 .ix

59.4.承受均布压力的矩形板的屈曲:与压力方向垂直的两对边 简支,而沿其余的两边有各种的边界条件………381 9.5.两对边简支井在与这两边平行的方向均匀受压的矩形板 $9.6.在弯曲与压缩联合作用下简支短形板的屈曲…396 9.7.在剪应力作用下矩形板的屈曲403 9.8.矩形板屈曲的其他情形410 9.9.圆板的屈曲413 9.10.其他形状的板的屈曲416 9.11.以肋条加强的板的稳定性418 $9.12.超过比例极限的板的屈曲…435 $9.13.屈曲板的大挠度437 $9.14.屈曲板的极限强度..445 $9.15.板的屈曲实验.451 $9.16.板屈曲理论的实际应用457 第十章薄壳的弯曲………468 $10.1.壳上体元的变形468 10.2.圆柱形壳的对称变形…471 10.3.圆柱形壳的无伸长的变形…473 $10.4.柱形壳的变形的一般情形477 10.5.球形壳的对称变形 482 第十一章壳的屈曲………486 11.1.圆柱形壳在均匀轴向压缩下的对称屈曲…486 $11.2.圆柱形壳由于不稳定性的无伸长弯曲形式………490 $11.3.在均匀轴向压力作用下圆柱形壳的屈曲(一般情形)……491 11.4.圆柱形壳轴向受压的实验497 $11.5.均匀横向外压作用下圆柱形壳的屈曲503 $11.6.受弯曲的或偏心受压的圆柱形壳…512 11.7.曲薄板的轴向压缩516 11.8.在剪力或剪力与轴向应力共同作用下的曲薄板…519 $11.9.在轴向压缩下加劲柱壳的屈曲521 11.10.在轴向压力与均匀横向压力共同作用下圆柱形壳的屈曲…526 11.11.受扭转的圆柱壳的屈曲…531

511,12,锥形壳的屈曲…541 511,13.均匀受压的球形壳的屈曲…545 附录 表A-1函数中(4),中(4),x(w)表……553 表A-2函数(4)与入(4)表…561 表A-3截面的性假………………562 内容索引…563 3 、 E ·xi

第一章 梁-柱 51.1.引营 在弯曲的初等理論中,梁的应力和挠度与作用的荷重成正比, 这要求梁由弯曲引超的变形不影响荷重的作用.例如,图1.1a中 只承受横向荷重(Q:与Q2)的梁,微小的挠度61与2及荷重的 铅直作用钱的稍微改变,对弯矩与剪力的影响无关紧要,于是,就 可以在梁的原有形状的基 础上,来計算挠度、应力与 弯矩等等在这些条件下, 并設材料服从胡克定律, (a) 則挠度与作用的荷重成正 比,且迭加原理可以适用: 1Q2 即最終的变形为各荷重单 独所产生的变形之和. (6) 当軸向和横向荷重同 图1.1 时作用于梁时(图1.16),情况完全不同.梁的弯矩、剪力,应力及 挠度并不与軸向荷重的大小成比例;而且,它們的值与所产生的挠 度的大小有关,且轴向荷重作用的稍微偏心就对它們有很大的影 响。同时承受轴向压力和横向荷重的梁称为梁-柱。在这第一一章 内,将分析在各种支承与加截状况下具有对称横截面的梁-柱”. §12.梁-柱的微分方程 用以分析梁-柱的基本方程可由开究图1.2a中的梁而推出. 1)对于承受轴向拉力的粱的分析,可参阅Timoshenko,Strength of Materials, 3d ed.,part lI,p.41,D.Van Nostrand Company,Inec.,Princeton,N. J,1956. 1
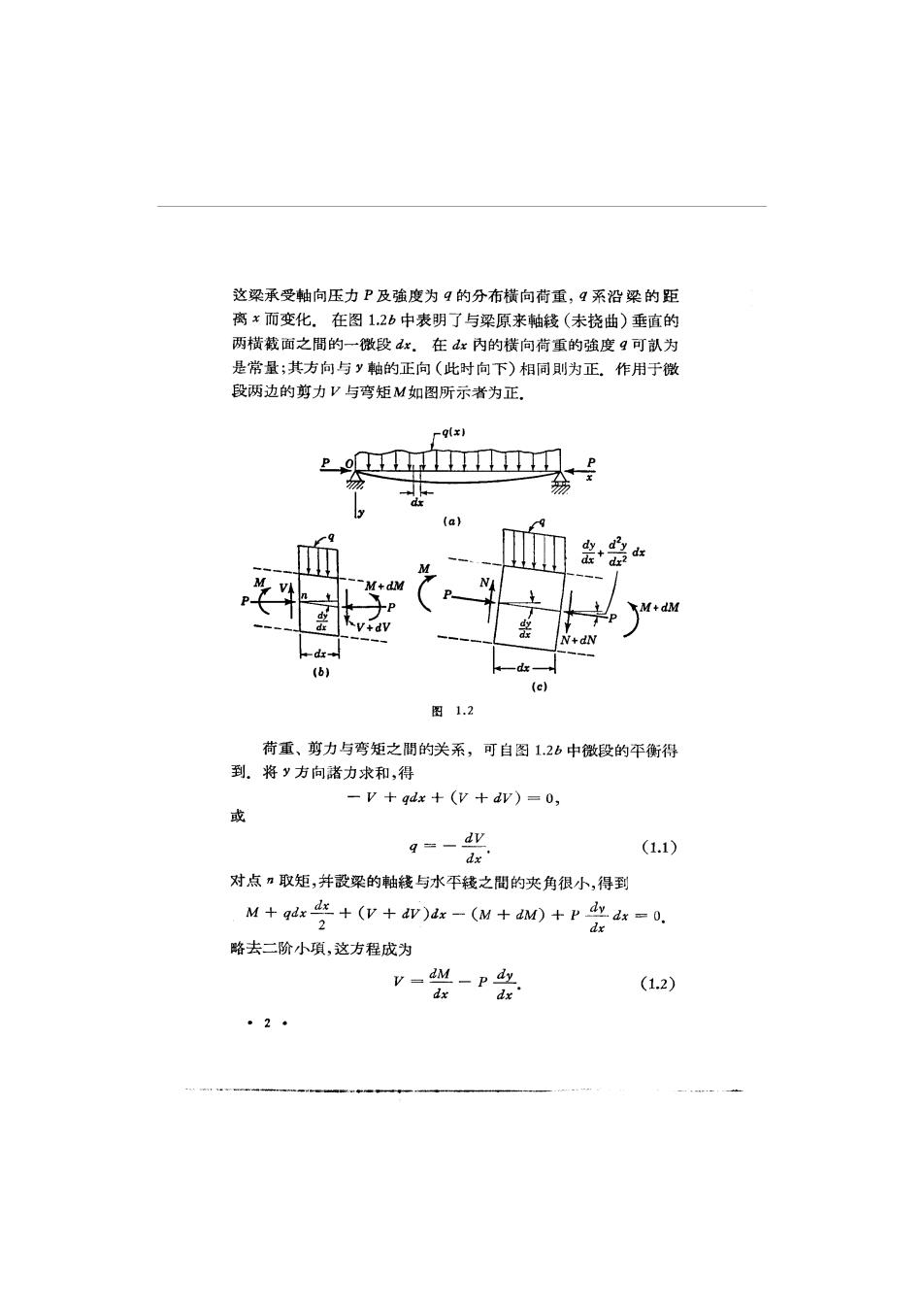
这梁承受軸向压力P及強度为4的分布横向荷重,9系沿染的距 离x而变化.在图12b中表明了与梁原来軸钱(未挠曲)垂直的 两横载面之間的一微段dx.在x内的横向荷重的強度g可认为 是常量;其方向与y軸的正向(此时向下)相同則为正。作用于微 段两边的剪力V与弯矩M如图所示者为正 -q(x) Po层 P (a) M+dM +dN dx (c) 图1.2 荷重、剪力与弯矩之間的关系,可自图1.2b中微段的平衡得 到。将y方向諸力求和,得 -v+qdx+(v+dv)=0, 或 9=、dy (1.1) dx 对点n取矩,并設梁的軸後与水不钱之間的夹角很小,得到 M+qdx+v)dx-(M+dM)+p4dx=0. 2 dx 略去二阶小項,这方程成为 vdM-p dy (1.2) dx dx 。2