
Ramsey理论
Ramsey 理论

Ramsey定理1(1930):给定正整数k和L,总存在一个最小正整数r(k,), 使得每个有(k,)个顶点的图,或者包含一个有k个点的团,或者包含一个有 (个点的独立集。 易见,r(1,)=r(k,1)=1r(2,)=((k,2)=2。 r(k,)称为 Ramsey数: 最小的正整数N,使得对完全图Kx的边任意红蓝二着色,总存在一个红色的 K或者存在一个蓝色的K
Ramsey 定理 1 (1930): 给定正整数k和 ,总存在一个最小正整数r k( , ), 使得每个有r k( , )个顶点的图,或者包含一个有k个点的团,或者包含一个有 个点的独立集。 易见,r r k r r k (1, ) ( ,1) 1; (2, ) , ( ,2) 2 = = = = 。 r k( , )称为 Ramsey 数: 最小的正整数 N,使得对完全图KN 的边任意红蓝二着色,总存在一个红色的 Kk或者存在一个蓝色的K
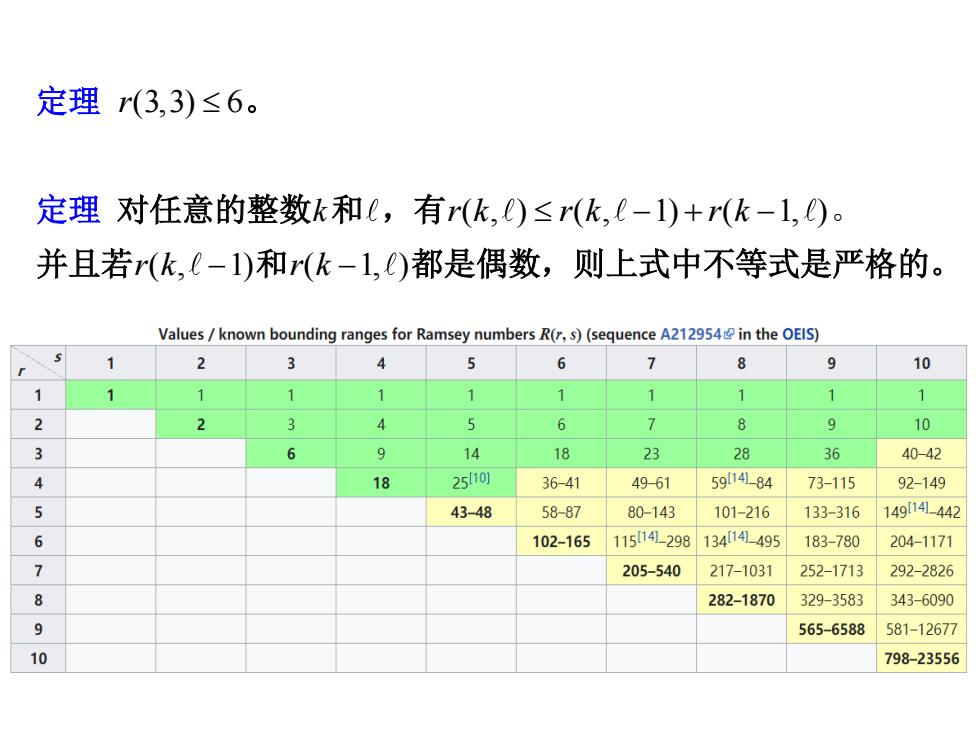
定理r(3,3)≤6。 定理对任意的整数k和L,有(k,)≤(k,(-1)+(k-1,)。 并且若r(k,(-1)和(飞-1,)都是偶数,则上式中不等式是严格的。 Values known bounding ranges for Ramsey numbers R(r,s)(sequence A212954 in the OEIS) 2 3 6 9 10 1 1 1 2 1 1 1 2 3 6 7 9 10 6 9 14 18 23 28 36 40-42 4 18 25f101 36-41 49-61 5914184 73-115 92-149 43-48 58-87 80-143 101-216 133-316 149[149-442 6 102-165 115141-298134[141-495 183-780 204-1171 205-540 217-1031 252-1713 292-2826 282-1870 329-3583 343-6090 9 565-6588 581-12677 10 798-23556
定理 r(3,3) 6 。 定理 对任意的整数k和 ,有r k r k r k ( , ) ( , 1) ( 1, ) − + − 。 并且若r k( , 1) − 和r k( 1, ) − 都是偶数,则上式中不等式是严格的
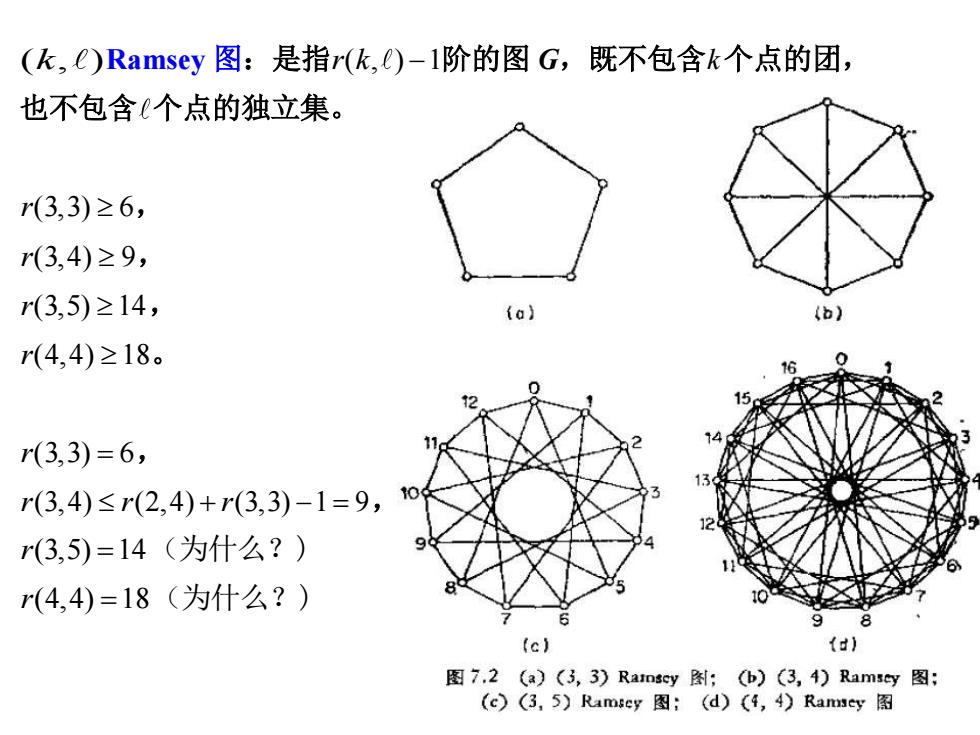
(k,C)Ramsey图:是指r(k,)-1阶的图G,既不包含k个点的团, 也不包含个点的独立集。 r(3,3)≥6, r(3,4)≥9, r(3,5)≥14, a】 (b r(4,4)≥18。 r(3,3)=6, 13 r(3,4)≤r(2,4)+r(3,3)-1=9,o r(3,5)=14(为什么?) r(4,4)=18(为什么?) 9 (c) (d) 图7.2(a)(3,3)Rarnsey:b)(3,4)Ramsey图: (c)(3,5)Ramsey图;(d)(4,4)Ramsey图
( , ) k Ramsey 图:是指r k( , ) 1− 阶的图 G,既不包含k个点的团, 也不包含 个点的独立集。 r(3,3) 6 , r(3,4) 9 , r(3,5) 14 , r(4,4) 18 。 r(3,3) 6 = , r r r (3,4) (2,4) (3,3) 1 9 + − = , r(3,5) 14 = (为什么?) r(4,4) 18 = (为什么?)
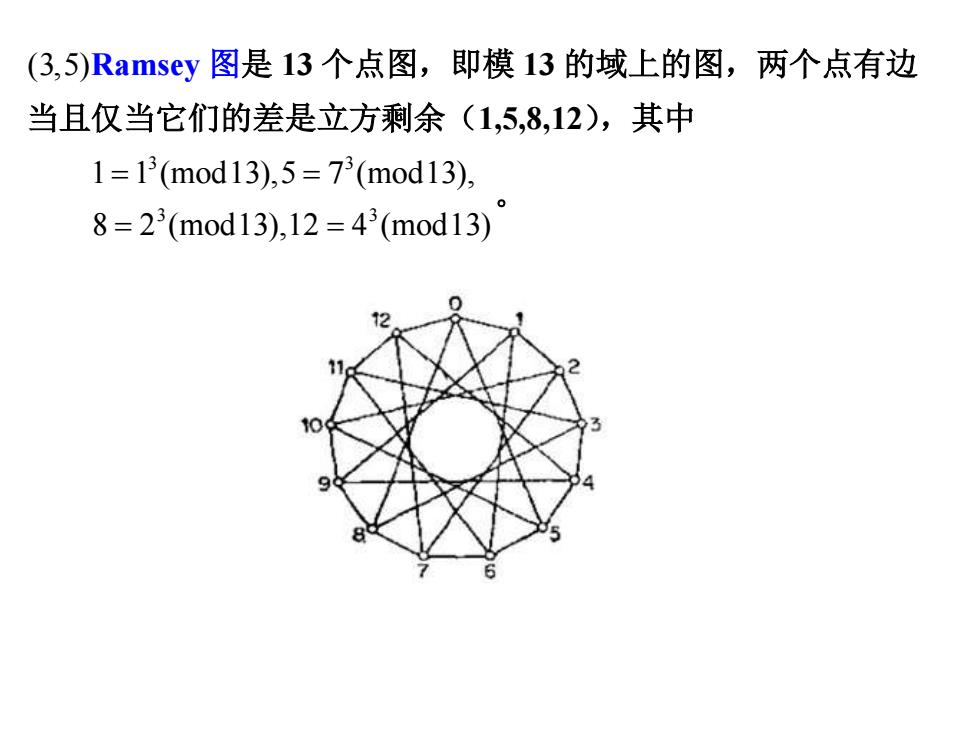
(3,5)Ramsey图是13个点图,即模13的域上的图,两个点有边 当且仅当它们的差是立方剩余(1,5,8,12),其中 1=1(mod13),5=73(mod13), 8=23(mod13),12=43(mod13)
(3,5)Ramsey 图是 13 个点图,即模 13 的域上的图,两个点有边 当且仅当它们的差是立方剩余(1,5,8,12),其中 3 3 3 3 1 1 (mod13),5 7 (mod13), 8 2 (mod13),12 4 (mod13) = = = =