
2016图论讨论班(七) 树与荫度
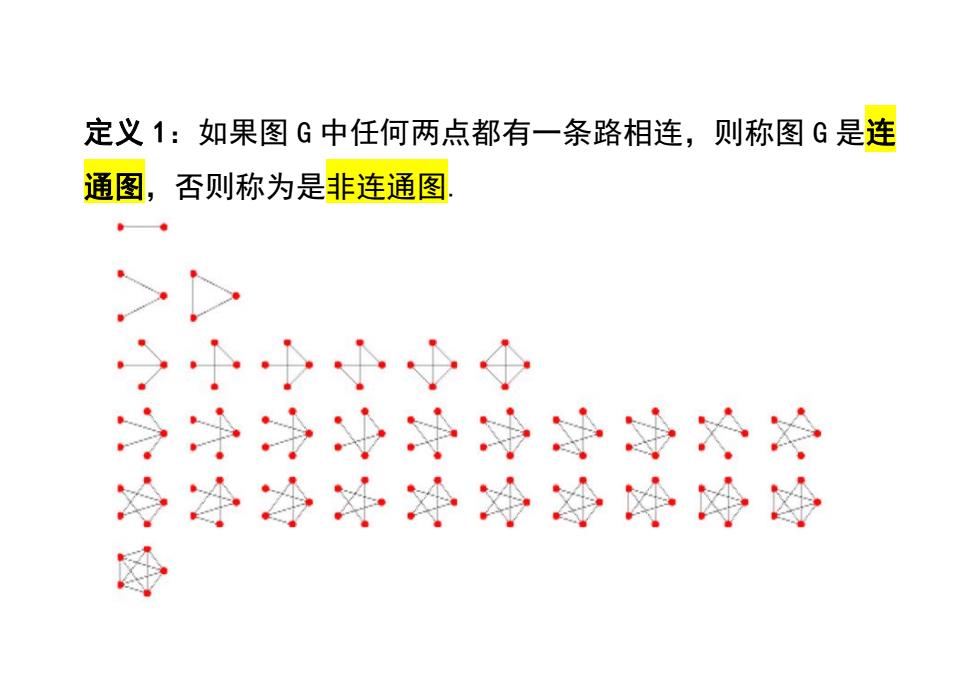
定义1:如果图G中任何两点都有一条路相连,则称图G是连 通图,否则称为是非连通图
定义 1:如果图 G 中任何两点都有一条路相连,则称图 G 是连 通图,否则称为是非连通图
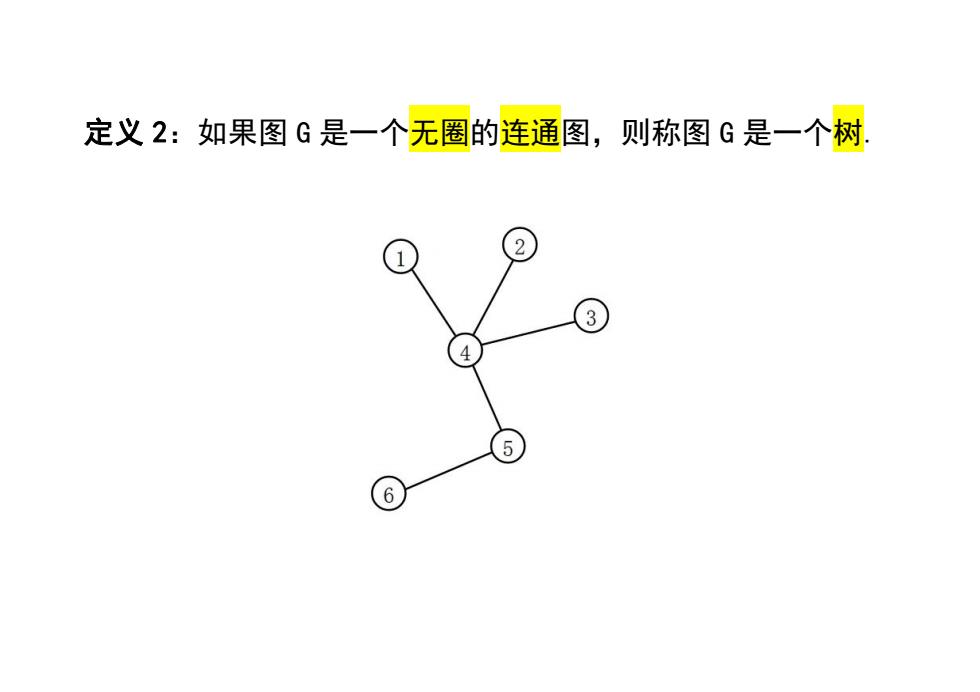
定义2:如果图G是一个无圈的连通图,则称图G是一个树 2 3 5 6
定义 2:如果图 G 是一个无圈的连通图,则称图 G 是一个树

定理1:设图G是一个具有n个顶点的连通图,则其边数 e≥n-1 证明:不妨设G是简单图(没有重边,没有环)。若n=1,则e=0, 结论成立!若G至少有2个顶点,则取V,={v,},则存在一条边e,∈ [V,V](边的一个端点属于V,另外一个端点属于V,的补)。记evV2, 则再取V2{v,V2}。 若V2是V(G)的真子集,则存在e2∈[V2,V2]。记ev2v3,则再取 V={v,V2,V}。按照这个过程继续下去,最后必定在取到n-1条边 e1,e,…,e1后得到集合V。={V1,V2,V3,…,Vn}=V(G),从而该迭代操作 终止。因此,图G至少有-1条边
定理 1:设图 G 是一个具有 n 个顶点的连通图,则其边数 e≥n-1 证明:不妨设 G 是简单图(没有重边,没有环)。若 n=1,则 e=0, 结论成立!若 G 至少有 2 个顶点,则取 V1 ={v1},则存在一条边 e1∈ [V1,V1](边的一个端点属于 V1,另外一个端点属于 V1的补)。记 e1 =v1v2, 则再取 V2={v1,v2}。 若 V2是 V(G)的真子集,则存在 e2∈[V2,V2]。记 e2=v2v3,则再取 V3 ={v1,v2,v3}。按照这个过程继续下去,最后必定在取到 n-1 条边 e1,e1,…,en-1后得到集合 Vn ={v1,v2,v3,…,vn}=V(G),从而该迭代操作 终止。因此,图 G 至少有 n-1 条边

定理2:设图T是一个具有n个顶点的树,则其边数e=-1, 证明:对n作数学归纳:当n=1时,T=K,从而e=0,结论成立! 假设当n=k时结论成立,下面考虑具有k+1个顶点的树T。 因为T不含有圈,并且连通,所以T的最小度恰好为1(为什 么?)。于是设T中有一条边uv,其中u的度数为1。 现将u从图T中删去,得到图T-u.容易看出,T-u必定无圈, 并且是连通的(为什么?)。也就是说,T-u是一个具有k+1-1=k个 顶点的树,从而由归纳假设,T-u有k-1条边。 因此,T有k-1+1=k条边!
定理 2:设图 T 是一个具有 n 个顶点的树,则其边数 e=n-1. 证明:对 n 作数学归纳:当 n=1 时,T=K1,从而 e=0,结论成立! 假设当 n=k 时结论成立,下面考虑具有 k+1 个顶点的树 T。 因为 T 不含有圈,并且连通,所以 T 的最小度恰好为 1(为什 么?)。于是设 T 中有一条边 uv,其中 u 的度数为 1。 现将 u 从图 T 中删去,得到图 T-u.容易看出,T-u 必定无圈, 并且是连通的(为什么?)。也就是说,T-u 是一个具有 k+1-1=k 个 顶点的树,从而由归纳假设,T-u 有 k-1 条边。 因此,T 有 k-1+1=k 条边!