
2016图论讨论班(五) 欧拉公式与牧转移方法
2016图论讨论班(五) 欧拉公式与权转移方法
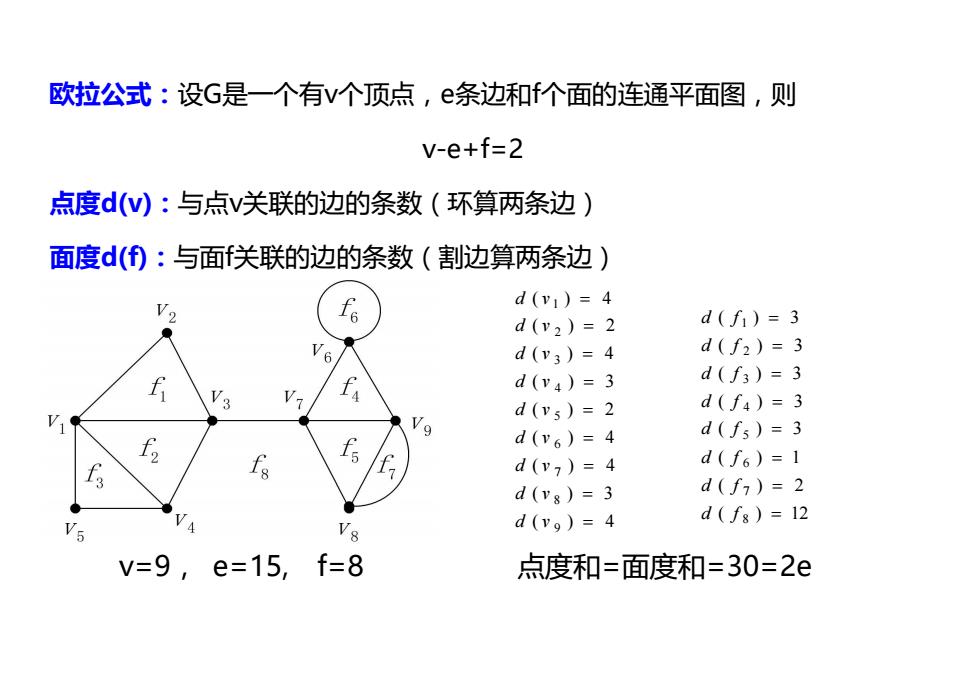
欧拉公式:设G是一个有v个顶点,e条边和f个面的连通平面图,则 v-e+f=2 点度d(W):与点v关联的边的条数(环算两条边) 面度d(⑤:与面关联的边的条数(割边算两条边) d(v1)=4 -6 d(v2)=2 d(f1)=3 d(v3)=4 d(f2)=3 d(v4)=3 d(f3)=3 19 d(v5)=2 d(f4)=3 d(v6)=4 d(fs)=3 Is d(v,)=4 d(f6)=1 d(vs)=3 d(f7)=2 d(fg)=12 V8 d(vo)=4 V=9,e=15,f=8 点度和=面度和=30=2e
欧拉公式:设G是一个有v个顶点,e条边和f个面的连通平面图,则 v-e+f=2 点度d(v):与点v关联的边的条数(环算两条边) 面度d(f):与面f关联的边的条数(割边算两条边) ( ) 4 ( ) 3 ( ) 4 ( ) 4 ( ) 2 ( ) 3 ( ) 4 ( ) 2 ( ) 4 9 8 7 6 5 4 3 2 1 d v d v d v d v d v d v d v d v d v ( ) 12 ( ) 2 ( ) 1 ( ) 3 ( ) 3 ( ) 3 ( ) 3 ( ) 3 8 7 6 5 4 3 2 1 d f d f d f d f d f d f d f d f v=9, e=15, f=8 点度和=面度和=30=2e

定理:设G是一个连通平面图,则对于任何实数k,>0,恒有: ∑(kd(v)-2k+10)+∑(ld(f)-2k+10)=-4k+1) v∈V(G) f∈F(G) 推论: ∑(d()-4)+∑(d(f)-4)=-8 vEV(G) f∈F(G) ∑(dy)-6)+∑(2d(f)-6)=-12 vEV(G) f∈F(G) 0●年布事●
定理:设G是一个连通平面图,则对于任何实数k,l>0,恒有: ( ) ( ) ( ( ) 2( )) ( ( ) 2( )) 4( ) v V G f F G kd v k l ld f k l k l 推论: ( ) ( ) ( ( ) 4) ( ( ) 4) 8 v V G f F G d v d f ( ) ( ) ( ( ) 6) (2 ( ) 6) 12 v V G f F G d v d f …………

四色定理的证明概述(每个平面图都是4-顶点可染的) 第一部分:(权转移方法) 证明每个平面图都含有若干种构型中的其中一个! 此部分使用的是理论性的数学证明! 第二部分:(可约性验证) 假设四色定理不正确,则其必然存在反例,即一个不是4-顶点可 染的平面图G,接下来证明图G不含有上述提及的任何一个构型! 此部分使用的是计算机证明,耗时1200小时!
四色定理的证明概述(每个平面图都是4-顶点可染的) 第一部分:(权转移方法) 证明每个平面图都含有若干种构型中的其中一个! 此部分使用的是理论性的数学证明! 第二部分:(可约性验证) 假设四色定理不正确,则其必然存在反例,即一个不是4-顶点可 染的平面图G,接下来证明图G不含有上述提及的任何一个构型! 此部分使用的是计算机证明,耗时1200小时!

权转移方法:一个例子 每个最小度为5的平面简单图,都含有以下两种构型之一: (1)一条边uv,其中d(u=5,d(W=5; (2)一条边uv,其中d(u)=5,d()=6. 证明:假设该命题的结论不对!即存在一个最小度为5的平面简单图G, 其不含有上述两种构型。 由于G的最小度为5,因此G必定含有一条边uv,其中d(u)=5。 由于G不含有构型(1)与(2),d()≥7
权转移方法:一个例子 每个最小度为5的平面简单图,都含有以下两种构型之一: (1) 一条边uv,其中d(u)=5,d(v)=5; (2) 一条边uv,其中d(u)=5,d(v)=6. 证明:假设该命题的结论不对!即存在一个最小度为5的平面简单图G, 其不含有上述两种构型。 由于G的最小度为5,因此G必定含有一条边uv,其中d(u)=5。 由于G不含有构型(1)与(2), d(v)≥7