
导航 仔)由V锥体=3Sh,可知三棱锥的任何一个面都可以作为底 面.(√) (4)若一个圆柱和一个六棱锥,它们的底面积相等、高相等,则 圆柱的体积一定是六棱锥体积的3倍.(√)
导航 (3)由V锥体= S·h,可知三棱锥的任何一个面都可以作为底 面.( ) (4)若一个圆柱和一个六棱锥,它们的底面积相等、高相等,则 圆柱的体积一定是六棱锥体积的3倍.( ) 𝟏 𝟑
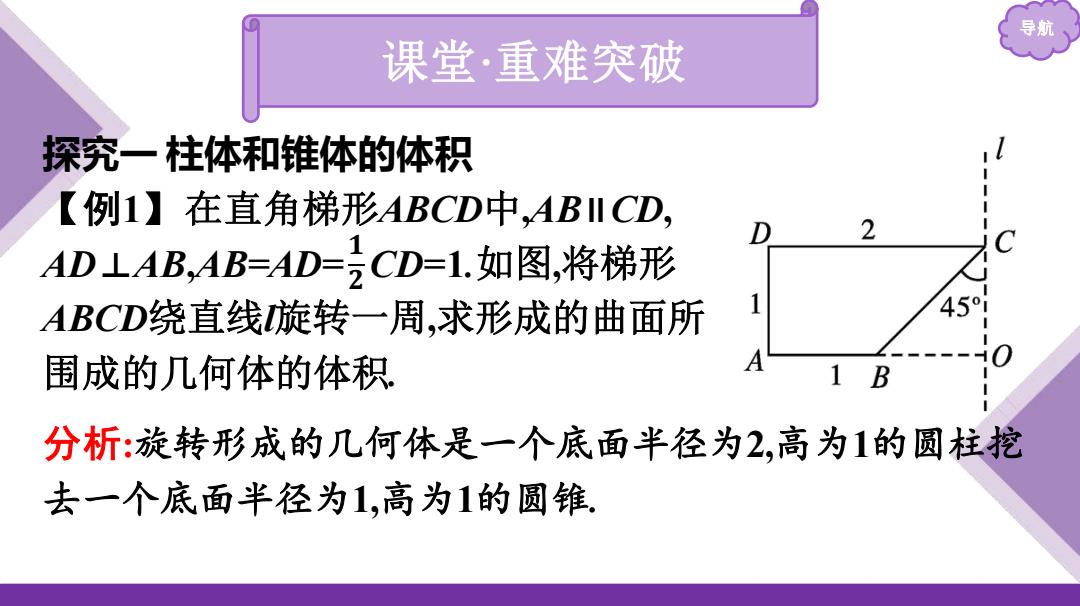
导航 课堂·重难突破 探究一柱体和锥体的体积 【例1】在直角梯形ABCD中,ABII CD, 2 AD⊥AB,AB=AD=CD=1.如图,将梯形 ABCD绕直线旋转一周,求形成的曲面所 围成的几何体的体积 B 分析:旋转形成的几何体是一个底面半径为2,高为1的圆柱挖 去一个底面半径为1,高为1的圆锥
导航 课堂·重难突破 探究一 柱体和锥体的体积 【例1】在直角梯形ABCD中,AB∥CD, AD⊥AB,AB=AD= CD=1.如图,将梯形 ABCD绕直线l旋转一周,求形成的曲面所 围成的几何体的体积. 分析:旋转形成的几何体是一个底面半径为2,高为1的圆柱挖 去一个底面半径为1,高为1的圆锥. 𝟏 𝟐

解:延长AB交1于点O(图略),矩形AOCD绕直线旅转一周形 成圆柱,其中底面半径R=2,高H=1, 则圆柱体积V=πR2H=4π. Rt△BOC绕直线l旋转一周形成圆锥,其中底面半径=1,高h=1, 则圈锥体积V号2h罗 因此所得几何体的体积为VV=4π-3 11π 3
导航 解:延长AB交l于点O (图略), 矩形AOCD绕直线l旋转一周形 成圆柱,其中底面半径R=2,高H=1, 则圆柱体积V=πR2H=4π. Rt△BOC绕直线l旋转一周形成圆锥,其中底面半径r=1,高h=1, 则圆锥体积 V'=𝟏 𝟑 𝛑r 2 h=𝛑 𝟑 , 因此所得几何体的体积为 V-V'=4π- 𝛑 𝟑 = 𝟏𝟏𝛑 𝟑

导期 延伸探究 将例1中的直角梯形绕CD所在直线旋转一周,求形成的曲面 所围成的几何体的体积. 解:由题意知,旋转形成的几何体是底面半径都为1,高都为1的 一个圆柱和一个圆锥,故所得几何体的体积 =nx1x1号×x12x1-
导航 将例1中的直角梯形绕CD所在直线旋转一周,求形成的曲面 所围成的几何体的体积. 解:由题意知,旋转形成的几何体是底面半径都为1,高都为1的 一个圆柱和一个圆锥,故所得几何体的体积 V=π×12 ×1+ 𝟏 𝟑 ×π×12 ×1= 𝟒𝛑 𝟑

导航 反思感悟 根据公式求柱体、锥体的体积,关键是求底面积.底面积的求 解要根据平面图形的性质灵活处理,熟记常见平面图形面积 的求法
导航 根据公式求柱体、锥体的体积,关键是求底面积.底面积的求 解要根据平面图形的性质灵活处理,熟记常见平面图形面积 的求法