
实验三多元和非线性回归模型 【实验目的】 本章是在第二章基础上的推广,仍然是学习计量经济学的重要基础。要求掌握多元线性 回归模型的矩阵估计方法,理解模型的参数估计以及模型的统计检验与简单线性回归的区 别:熟悉模型的非线性特征,掌握非线性模型的两类估计方法。在本实验结束后,学生能够 根据所学知识,独立地选择实际经济问题,确定研究对象,按照计量经济分析的工作程序(即 建立理论模型,收集统计数据,参数的估计和检验),最终写出研究分析报告。 【实验内容】 一、建立西部电力消费多元回归模型(2-3-1.1) 二、建立中国税收收入多元回归模型(23-2.1) 三、建立中国的生产函数(模型)(2-3-3.wf1) 【实验步骤】 一、建立西部电力消费多元回归模型(2-3-1.wf1) 问题概述:研究西部各省份2002年电力消费量(Y,亿千瓦小时)与国内生产总值(X, 亿元)、水电燃料价格指数(X,%)的数量关系。 1.用矩阵命令构造X和Y矩阵(见图2-3-1): 日▣☒ File Edit Object Yiew Eroc Quick Options Window Help up groupxx1 x2x3 ☐orkfi1e:2-31-(e:计量课本数据.回☒ sample:111-11 obs Display Filter 回groupx 粤sigma2 Path d:\ny docunents DB=none WF=2-3-1 图2-3-1命令窗口中使用矩阵命令 natrix matrixy=econvert(y)‘将Y序列转换为矩阵类型 series xl=‘建立一个值为1的序列 30
20 实验三 多元和非线性回归模型 【实验目的】 本章是在第二章基础上的推广,仍然是学习计量经济学的重要基础。要求掌握多元线性 回归模型的矩阵估计方法,理解模型的参数估计以及模型的统计检验与简单线性回归的区 别;熟悉模型的非线性特征,掌握非线性模型的两类估计方法。在本实验结束后,学生能够 根据所学知识,独立地选择实际经济问题,确定研究对象,按照计量经济分析的工作程序(即 建立理论模型,收集统计数据,参数的估计和检验),最终写出研究分析报告。 【实验内容】 一、建立西部电力消费多元回归模型(2-3-1.wf1) 二、建立中国税收收入多元回归模型(2-3-2.wf1) 三、建立中国的生产函数(模型)(2-3-3.wf1) 【实验步骤】 一、建立西部电力消费多元回归模型(2-3-1.wf1) 问题概述:研究西部各省份 2002 年电力消费量(Y,亿千瓦·小时)与国内生产总值( X2 , 亿元)、水电燃料价格指数( X3 ,%)的数量关系。 1.用矩阵命令构造 X 和 Y 矩阵(见图 2-3-1); 图 2-3-1 命令窗口中使用矩阵命令 matrix matrixy=@convert(y) ‘将 Y 序列转换为矩阵类型 series x1=1 ‘建立一个值为 1 的序列

group groupx x1x2x3‘建立一个名称为gTOUpx的数组,包括三个序列 matrix matrixx=convert(groupx)‘将groupx数组转换为矩阵 2.用矩阵云算函数完成对模型参数的估计(见图2-3-2): matrix xx=-transpose(matrixx))*matrixx‘求出参数估计公式的前半部分 阳trix xy=etranspose(atrix)*natrixy‘求出参数估计公式的后半部分 matrix b=@inverse(xx)*xy‘得到参数矩阵 日▣☒ File Edit Object View Proc Quick Options Window Help Yorkfi1e:2-31-(e:计量课本数据.:日回☒ View Procobject Print Save Detais+Show Fetch Store Delete Ge Display Filter. Path d:\ny documents DB none WF 2-3-1 图2-3-2矩阵运算函数 双击工作文件窗口中的矩阵b,即可得到估计出的三个参数(图2-3-3),估计出的模型 为:y=1941.837+0.094X2-17.151X+ ☐orkf☐Hatrix:B Workfi1e:2-3-1 ew Proc OE View Procobject Print Name Freeze Edit+ B mple:1 C1 Last updated:07 R1 1941837 量mata 图2-3-3矩阵命令计算出的参数向量b 3.用矩阵运算完成方程方差估计和可决系数的计算(见图2-3-4)。 残差平方和的矩阵计算公式:RSS=Yy-BXY,多重可决系数参考公式(1-2-38) matrix RSS=8transpose(matrixy)*matrixy-@transpose(b)*etranspose(matrixx)*matrixy 算残差平方和
21 group groupx x1 x2 x3 ‘建立一个名称为 groupx 的数组,包括三个序列 matrix matrixx=@convert(groupx) ‘将 groupx 数组转换为矩阵 2.用矩阵运算函数完成对模型参数的估计(见图 2-3-2); matrix xx=@transpose(matrixx)*matrixx ‘求出参数估计公式的前半部分 matrix xy=@transpose(matrixx)*matrixy ‘求出参数估计公式的后半部分 matrix b=@inverse(xx)*xy ‘得到参数矩阵 图 2-3-2 矩阵运算函数 双击工作文件窗口中的矩阵 b,即可得到估计出的三个参数(图 2-3-3),估计出的模型 为: 2 3 1941.837 0.094 17.151 Yi = + X i - + X u i i 图 2-3-3 矩阵命令计算出的参数向量 b 3.用矩阵运算完成方程方差估计和可决系数的计算(见图 2-3-4)。 RSS = - Y 'Y b ' ' X Y ) 残差平方和的矩阵计算公式: ,多重可决系数参考公式(1-2-38)。 matrix RSS=@transpose(matrixy)*matrixy-@transpose(b)*@transpose(matrixx)*matrixy ‘计 算残差平方和
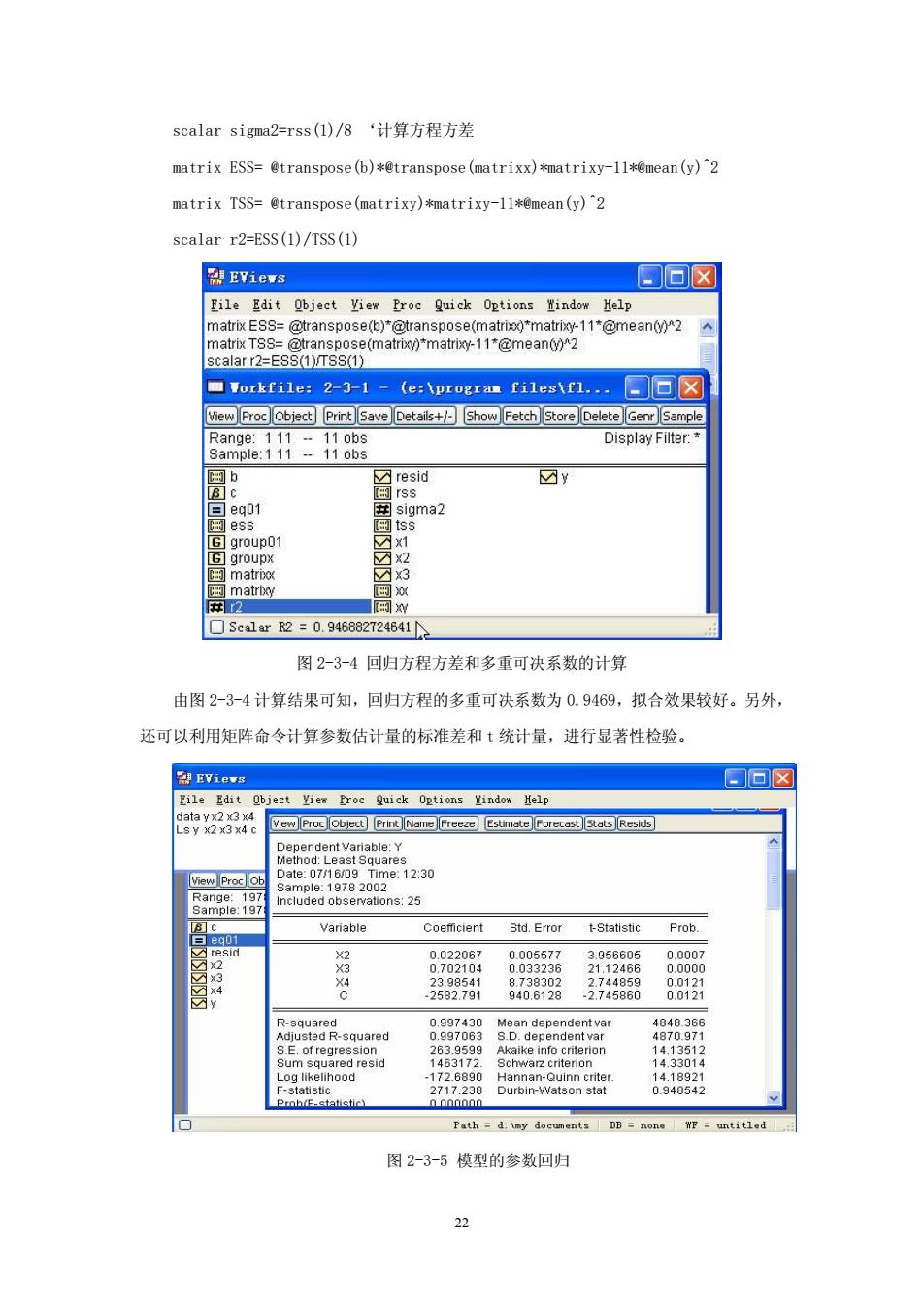
scalar sigma2=rss()/8‘计算方程方 matrix ESS=@transpose(b)*@transpose(matrixx)*matrixy-11*@mean(y)2 matrix TSS=@transpose(matrixy)*matrixy-11*mean(y)'2 scalar r2=ESS(1)/TSS(1) EVievs File Edit Obiect Vies Proc Quick Options Help @transpose(matrbo)"matry-11@mean()2 e(matri)"matrig-11*@mean()2 □orkfi1e:2-3-1-(e:program fi1egf1.□回☒ view Procobject Print Save Detais+Show Fetch Store Delete Display Fiter resid ☑y ☐5ca1ar2=0.94682724641 图2-3-4回归方程方差和多重可决系数的计算 由图2-3-4计算结果可知,回归方程的多重可决系数为0.9469,拟合效果较好。另外, 还可以利用矩阵命令计算参数估计量的标准差和t统计量,进行显著性检验。 2EViows ✉回☒ Eile Edit t View Proc Quick Options Yindow Help view Proc object Prin Name Freeze Estimate ForecasStats Resds s:25 Variable Std.Error Prob. red 8 2717238 Durbin-Watson stat 0948542 图2-3-5模型的参数回归
22 scalar sigma2=rss(1)/8 ‘计算方程方差 matrix ESS= @transpose(b)*@transpose(matrixx)*matrixy-11*@mean(y)^2 matrix TSS= @transpose(matrixy)*matrixy-11*@mean(y)^2 scalar r2=ESS(1)/TSS(1) 图 2-3-4 回归方程方差和多重可决系数的计算 由图 2-3-4 计算结果可知,回归方程的多重可决系数为 0.9469,拟合效果较好。另外, 还可以利用矩阵命令计算参数估计量的标准差和 t 统计量,进行显著性检验。 图 2-3-5 模型的参数回归
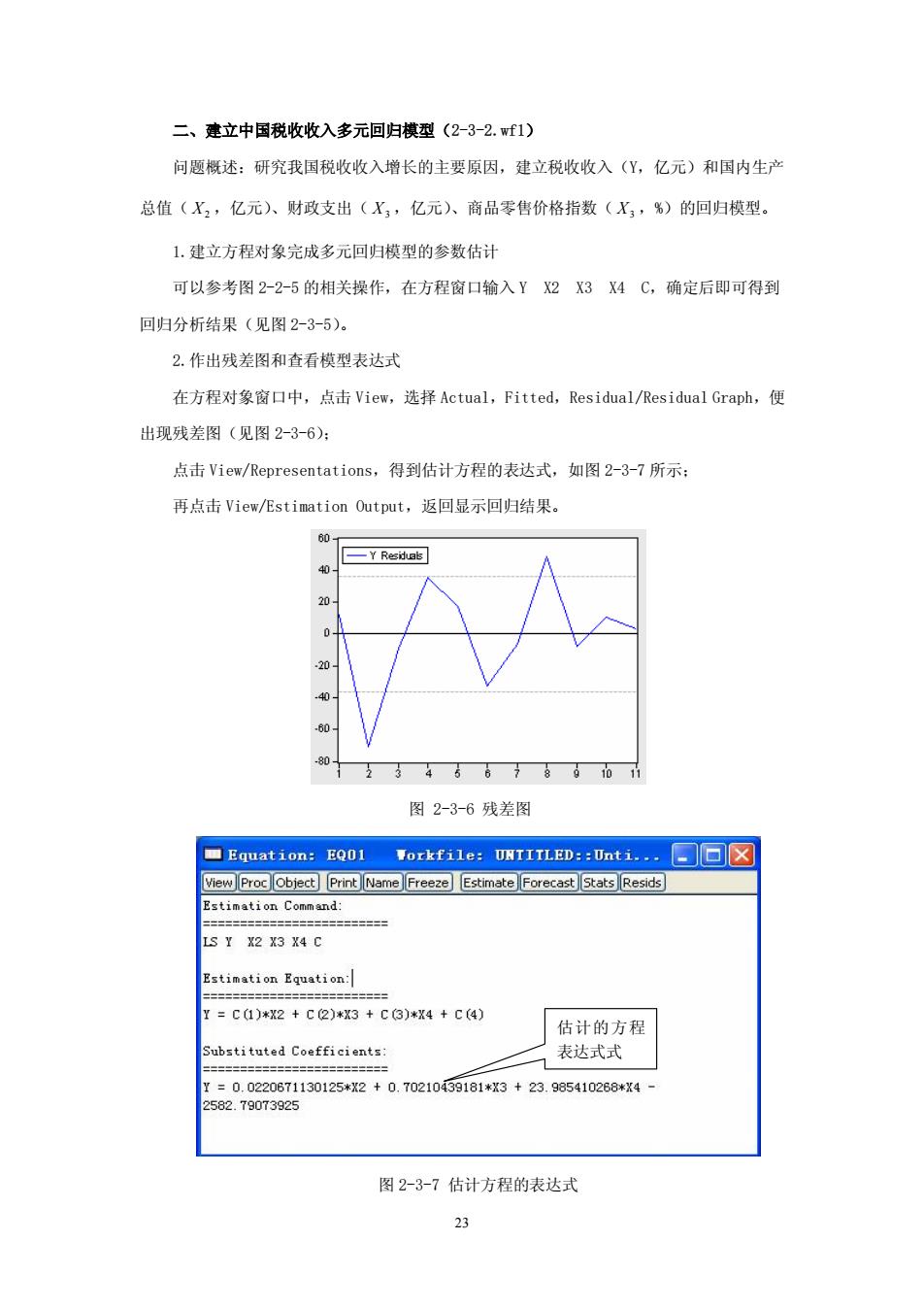
二、建立中国税收收入多元回归模型(2-3-2.f1) 问题概述:研究我国税收收入增长的主要原因,建立税收收入(了,亿元)和国内生产 总值(X2,亿元、财政支出(X,亿元、商品零售价格指数(X,%)的回归模型。 1.建立方程对象完成多元回归模型的参数估计 可以参考图2-2-5的相关操作,在方程窗口输入YX2X3X4C,确定后即可得到 回归分析结果(见图2-3-5). 2.作出残差图和查看模型表达式 在方程对象窗口中,点击View,选择Actual,Fitted,Residual/.Residual Graph,便 出现残差图(见图2-3-6): 点击View/Representations,得到估计方程的表达式,如图2-3-7所示: 再点击View/Esti服tion Output,返回显示回归结果 一YRsa电 00 图2-3-6残差图 口Equation::EQ01 orkfi1e:UNTITLED:0nti.回☒ Estimation Command: S Y X2 X3 X4 C Estimation Equation: ca)*2+c2)*3+c3)*x4+c4) 估计的方程 一气表达式式 7=0.0220671130125*2+0.702109181*X3+23.995410268*X4 .79073925 图2-3-7估计方程的表达式
23 二、建立中国税收收入多元回归模型(2-3-2.wf1) 问题概述:研究我国税收收入增长的主要原因,建立税收收入(Y,亿元)和国内生产 总值( X2 ,亿元)、财政支出( X3 ,亿元)、商品零售价格指数( X3 ,%)的回归模型。 1.建立方程对象完成多元回归模型的参数估计 可以参考图 2-2-5 的相关操作,在方程窗口输入 Y X2 X3 X4 C,确定后即可得到 回归分析结果(见图 2-3-5)。 2.作出残差图和查看模型表达式 在方程对象窗口中,点击 View,选择 Actual,Fitted,Residual/Residual Graph,便 出现残差图(见图 2-3-6); 点击 View/Representations,得到估计方程的表达式,如图 2-3-7 所示; 再点击 View/Estimation Output,返回显示回归结果。 图 2-3-6 残差图 图 2-3-7 估计方程的表达式 估计的方程 表达式式

3,对回归方程进行经济意义检验、拟合优度检验、F检验和t检验,并判断各检验的区 别与联系 (1)经济意义检验 模型估计结果说明,在假定其它变量不变的情况下,当年GDP每增长1亿元,税收收入 就会增长0.02207亿元:在假定其它变量不变的情况下,当年财政支出每增长1亿元,税收 收入会增长0.7021亿元:在假定其它变量不变的情况下,当年零售商品物价指数上涨一个 百分点,税收收入就会增长23.9854亿元。这与理论分析和经验判断相一致。 (2)统计检验 拟合优度:由图2-3-5中数据可以得到:R2=0.9974,修正的可决系数为R2=0.9971 这说明模型对样本的拟合很好。 F检验:针对H。:B=B;=B:=0,给定显著性水平a=0.05,在F分布表中查出自 由度为k-1=3和n-k=21的临界值F(3,2)=3.075。由图2-3-5中得到F=2717238,由于 大于临界值,应拒绝原假设,说明回归方程显著,即“国内生产总值”、“财政支出”、“商品 零售物价指数”等变量联合起来确实对“税收收入”有显著影响。 t检验:给定显著性水平,查t分布表得自由度为-k=21临界值112(n-k)=2.08。 由图2-3-5中数据可得,与参数对应的t统计量分别为-2.7459、3.9566、21.1247、2.7449 其绝对值均大于临界值,这说明分别都应当拒绝原假设,也就是说,当在其它解释变量不变 的情况下,解释变量“国内生产总值”、“财政支出”、“商品零售物价指数”分别对被解释变 量“税收收入”Y都有显著的影响。 4.对模型进行回归系数的区间估计并计算预测值的置信区间 参数估计的置信区间: p-,≤+aac=l-a 个别值预测区间:Yr-ta28、K,(XX)X,sy,≤r+ia26K,(XXX 参考实验二的命令方式计算过程。 三、建立中国生产函数(模型)(2-3-3.f1) 问题概述:研究我国1980~2002年国内生产总值(GDP,亿元)、劳动投入(L,万人) 资本投入(K,亿元)的数量关系。 1.建立我国柯布一道格拉斯生产函数 GDP=A*L严*KB 2.用线性化方法和迭代估计法完成模型的参数估计 24
24 3.对回归方程进行经济意义检验、拟合优度检验、F 检验和 t 检验,并判断各检验的区 别与联系 (1)经济意义检验 模型估计结果说明,在假定其它变量不变的情况下,当年 GDP 每增长 1 亿元,税收收入 就会增长 0.02207 亿元;在假定其它变量不变的情况下,当年财政支出每增长 1 亿元,税收 收入会增长 0.7021 亿元;在假定其它变量不变的情况下,当年零售商品物价指数上涨一个 百分点,税收收入就会增长 23.9854 亿元。这与理论分析和经验判断相一致。 (2)统计检验 拟合优度:由图 2-3-5 中数据可以得到: 0.9974 2 R = ,修正的可决系数为 0.9971 2 R = , 这说明模型对样本的拟合很好。 F 检验:针对 : 0 H0 b2 = b3 = b4 = ,给定显著性水平a = 0.05 ,在 F 分布表中查出自 由度为 k-1=3 和 n-k=21 的临界值 (3,21) = 3.075 Fa 。由图 2-3-5 中得到 F = 2717.238 ,由于 大于临界值,应拒绝原假设,说明回归方程显著,即“国内生产总值”、“财政支出”、“商品 零售物价指数”等变量联合起来确实对“税收收入”有显著影响。 t 检验:给定显著性水平,查 t 分布表得自由度为 n-k=21 临界值 ( ) 2.08 t a / 2 n - k = 。 由图 2-3-5 中数据可得,与参数对应的 t 统计量分别为-2.7459、3.9566、21.1247、2.7449, 其绝对值均大于临界值,这说明分别都应当拒绝原假设,也就是说,当在其它解释变量不变 的情况下,解释变量“国内生产总值”、“财政支出”、“商品零售物价指数”分别对被解释变 量“税收收入”Y 都有显著的影响。 4.对模型进行回归系数的区间估计并计算预测值的置信区间 参数估计的置信区间: b a s b b a s = -a ú ú ú û ù ê ê ê ë é - £ £ + Ù Ù Ù Ù P t / 2 c jj j t / 2 c jj 1 个别值预测区间: ' 1 ' / 2 ' 1 ' / 2 ( ) ( ) f f f f f f Y f t X X X X Y Y t X X X X - Ù Ù - Ù Ù - a d £ £ + a d 参考实验二的命令方式计算过程。 三、建立中国生产函数(模型)(2-3-3.wf1) 问题概述:研究我国 1980~2002 年国内生产总值(GDP,亿元)、劳动投入(L,万人)、 资本投入(K,亿元)的数量关系。 1.建立我国柯布-道格拉斯生产函数 a b GDP = A* L * K 2.用线性化方法和迭代估计法完成模型的参数估计