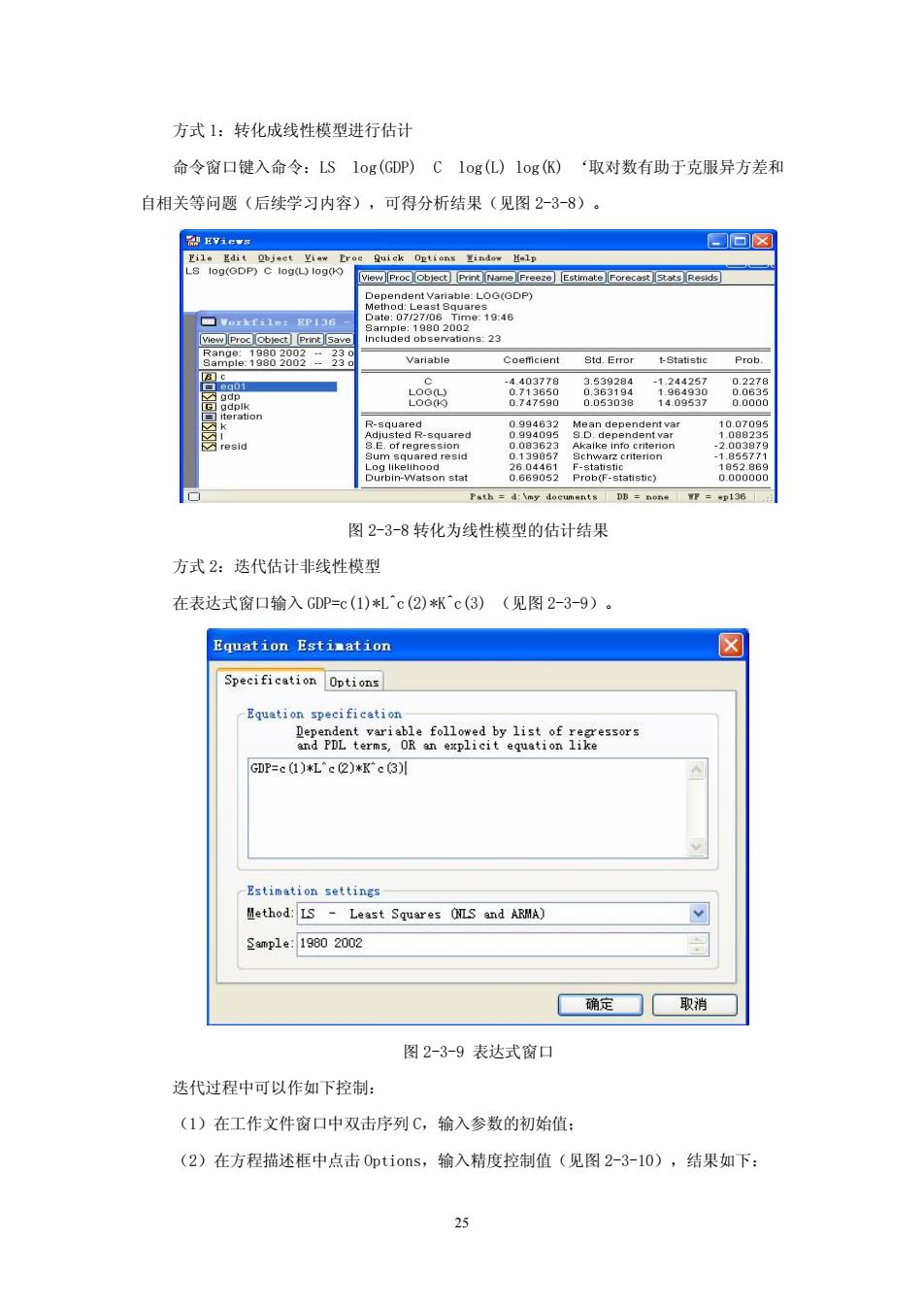
方式1:转化成线性模型进行估计 命令窗口健入命令:LS1og(GDP)C1og(L)1ogK)‘取对数有助于克服异方差和 自相关等问题(后续学习内容),可得分析结果(见图2-3-8)。 国回☒ 5。 8☏ 08g98 esid 图2-3-8转化为线性模型的估计结果 方式2:迭代估计非线性模型 在表达式窗口输入GDP=c(1)札c(2)林c(3)(见图2-3-9)。 Equation Estimation ☒ Specification Options Equation specification grtt股opi.:8 GDP=e ()*L'e (@)*K'c (3) Estimation setting &9mple:19602002 ■确定☐取消 图2-3-9表达式窗口 迭代过程中可以作如下控制: (1)在工作文件窗口中双击序列C,输入参数的初始值: (2)在方程描述框中点击0 ptions,输入精度控制值(见图2-3-10),结果如下:
25 方式 1:转化成线性模型进行估计 命令窗口键入命令:LS log(GDP) C log(L) log(K) ‘取对数有助于克服异方差和 自相关等问题(后续学习内容),可得分析结果(见图 2-3-8)。 图 2-3-8 转化为线性模型的估计结果 方式 2:迭代估计非线性模型 在表达式窗口输入 GDP=c(1)*L^c(2)*K^c(3) (见图 2-3-9)。 图 2-3-9 表达式窗口 迭代过程中可以作如下控制: (1)在工作文件窗口中双击序列 C,输入参数的初始值; (2)在方程描述框中点击 Options,输入精度控制值(见图 2-3-10),结果如下:
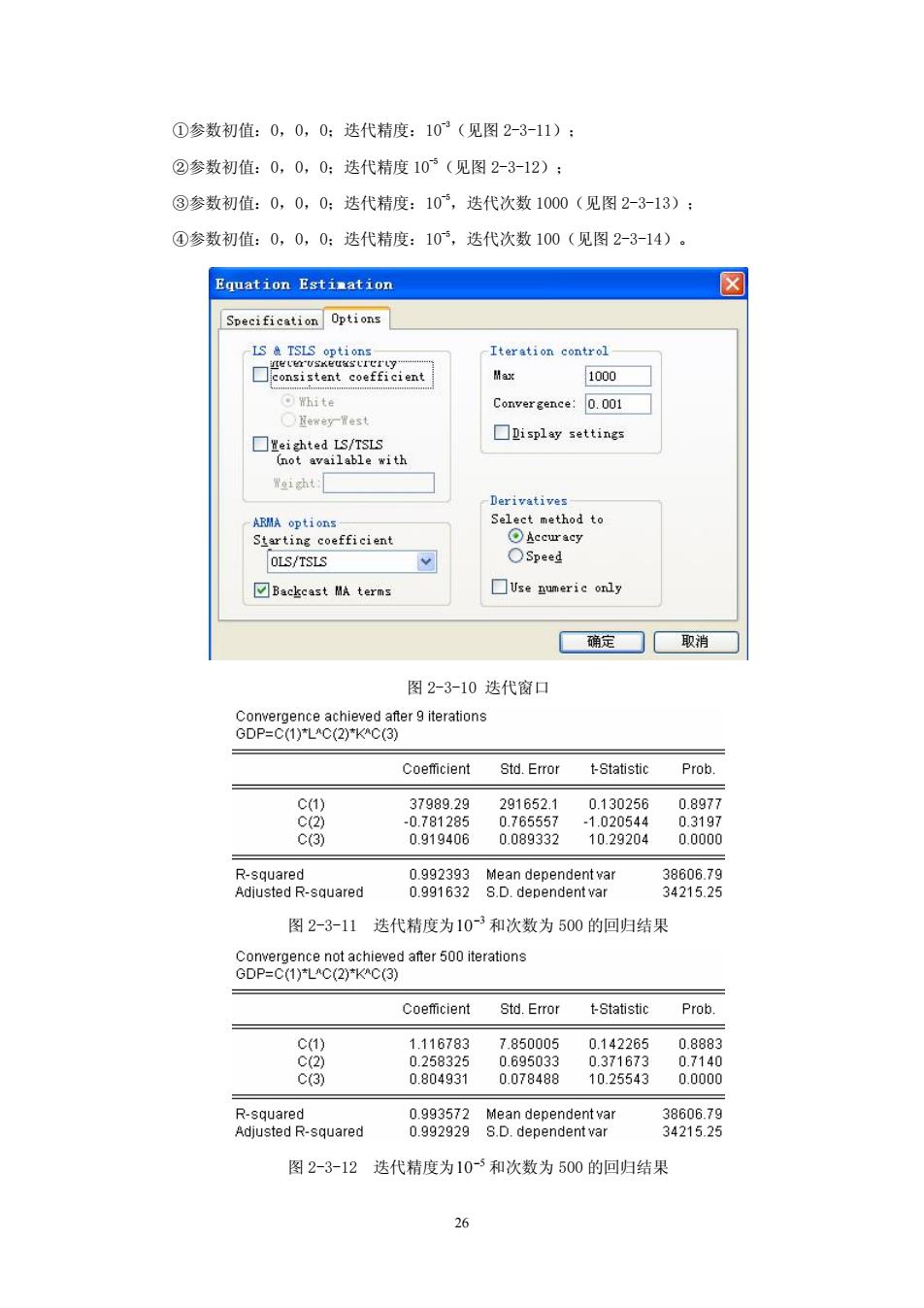
①参数初值:0,0,0:迭代精度:103(见图2-3-11): ②参数初值:0,0,0:达代精度10(见图2-3-12): ③参数初值:0,0,0:迭代精度:10°,迭代次数1000(见图2-3-13): ④参数初值:0,0,0:迭代精度:10,迭代次数100(见图2-3-14)。 Equation Estimntion ☒ Specification Options Iteration control 1000 White Convergence:0.001 Newey-Yest 口anta5eu ☐卫isplay settings Select method to OSpeed ☑Backcast MA terms ☐Use numeric only 确定☐取消 图2-3-10迭代窗口 Coeficient Std.Error tStatistic Prob. -1.02 702920 uuared 89878938ean88a8mtar 图2-3-11迭代精度为10-3和次数为500的回归结果 Coefficient Std.Error t-Statistic Prob. c() 1.116783 7.850005 0.14226 0.8885 c() 0.804931 0078488 1025543 000m R-squared 38606.79 Adjusted R-squared 34215.25 图2-3-12迭代精度为10-5和次数为500的回归结果
26 ①参数初值:0,0,0;迭代精度:10-3(见图 2-3-11); ②参数初值:0,0,0;迭代精度 10-5(见图 2-3-12); ③参数初值:0,0,0;迭代精度:10-5,迭代次数 1000(见图 2-3-13); ④参数初值:0,0,0;迭代精度:10-5,迭代次数 100(见图 2-3-14)。 图 2-3-10 迭代窗口 图 2-3-11 迭代精度为 3 10- 和次数为 500 的回归结果 图 2-3-12 迭代精度为 5 10- 和次数为 500 的回归结果

Coefficient Std.Error t-Statistic Prob. 0042168 0293431 0.143705 0.887 0.770120 0.077039 9.996503 0.000d R-squared Adiusted R-squared 图2-3-13迭代精度为105和次数为1000的回归结果 0p8288aegaer1o0eraong Std.Error t-Statistic Prob. 896 .087417 0.392 0.905457 0.087661 10.32908 0.0000 图2-3-14迭代精度为105和次数为100的回归结果 从4个回归结果中看出,C(2)的系数全都不显著,并且由图2-3-8结果中得出可决系数 R2=0.9946,都比迭代法的可决系数大,由此可见,采用线性化方法估计模型更为合适(在 不考虑模型可能存在的自相关的情况下)。 3.根据劳动和资本投入弹性值判断规模报酬情况。 由图2-3-8可知,a=0.71和B=0.75,a+B=146>1,所以可以初步判断该函数是 规模报酬递增。 四、Eviews中的矩阵运算函数简介 l,矩阵的定义:Matrix::对称矩阵的定义:sym:向量定义:vector 2.序列、群向矩阵的转换:Matrix y=Econvert(x) 3.矩阵的转置:@transpose0 4.矩阵逆的运算:@inverse0 【练习与作业】 1.美国30所知名学校的MBA学生1994年基本年薪(ASP)、GPA分数(从1广4共四个 等级)、GMAT分数以及每年学费(ATT)的数据。(数据见电子附件1x3-1.wf1) (1)建立一个多元回归模型,解释B弘毕业生的平均初职工资,并且求出回归结果: 27
27 图 2-3-13 迭代精度为 5 10- 和次数为 1000 的回归结果 图 2-3-14 迭代精度为 5 10- 和次数为 100 的回归结果 从 4 个回归结果中看出,C(2)的系数全都不显著,并且由图 2-3-8 结果中得出可决系数 0.9946 2 R = ,都比迭代法的可决系数大,由此可见,采用线性化方法估计模型更为合适(在 不考虑模型可能存在的自相关的情况下)。 3.根据劳动和资本投入弹性值判断规模报酬情况。 由图 2-3-8 可知,a = 0.71和 b = 0.75,a + b =1.46 >1,所以可以初步判断该函数是 规模报酬递增。 四、Eviews 中的矩阵运算函数简介 1.矩阵的定义:Matrix;对称矩阵的定义:sym;向量定义:vector 2.序列、群向矩阵的转换:Matrix y=@convert(x) 3.矩阵的转置:@transpose() 4.矩阵逆的运算:@inverse() 【练习与作业】 1.美国 30 所知名学校的 MBA 学生 1994 年基本年薪(ASP)、GPA 分数(从 1~4 共四个 等级)、GMAT 分数以及每年学费(ATT)的数据。(数据见电子附件 lx3-1.wf1) (1)建立一个多元回归模型,解释 MBA 毕业生的平均初职工资,并且求出回归结果;

(2)如果模型中包括了GPA和GMAT分数这两个解释变量,先验地,你可能会遇到什么 问题,为什么? (3)如果学费这一变量的系数为正、并且在统计上是显若的,是否表示进入最昂贵的 商业学校是值得的。学费这个变量可用什么来代替 2.考察家庭月收入与购买耐用消费品的关系,用Y表示虚拟变量,取1时表示已购买, 0表示没有购买,可用逻辑增长曲线建立计量模型。(数据见电子附件1x3-2.wf1) 3.1960-1982年7个0ECD国家(美国、加拿大、德国、意大利、英国、日本、法国) 总的最终能源需求指数(y)、实际的GDP(x)人、实际的能源价格(x2)的数据,所有指数 均以及970年为基准(1970=100),试建立模型对能源需求和两个影响因素间的关系进行分 析。(数据见电子附件1x3-3.wf1) ①运用柯布一道格拉斯生产函数建立能源需求与收入、价格之间的对数需求函数 Iny,=bo+b Inxy+bInx+ ②所估计的回归系数是否显著?用P值回答这个问题。 ③解释回归系数的意义。 ④根据上面的数据建立线性回归模型: y:=bo+bu+bx+u ⑤比较以上两个模型的可决系数 ©如果以上两个模型的结论不同,你将选择哪一个回归模型?为什么?
28 (2)如果模型中包括了 GPA 和 GMAT 分数这两个解释变量,先验地,你可能会遇到什么 问题,为什么? (3)如果学费这一变量的系数为正、并且在统计上是显著的,是否表示进入最昂贵的 商业学校是值得的。学费这个变量可用什么来代替? 2.考察家庭月收入与购买耐用消费品的关系,用Y 表示虚拟变量,取 1 时表示已购买, 0 表示没有购买,可用逻辑增长曲线建立计量模型。(数据见电子附件 lx3-2.wf1) 3. 1960-1982 年 7 个 OECD 国家(美国、加拿大、德国、意大利、英国、日本、法国) 总的最终能源需求指数( y )、实际的 GDP( 1 x )、实际的能源价格( 2 x )的数据,所有指数 均以及 970 年为基准(1970=100),试建立模型对能源需求和两个影响因素间的关系进行分 析。(数据见电子附件 lx3-3.wf1) ①运用柯布-道格拉斯生产函数建立能源需求与收入、价格之间的对数需求函数: t t t t y = b + b x + b x + u 0 1 1 2 2 ln ln ln ②所估计的回归系数是否显著?用 p 值回答这个问题。 ③解释回归系数的意义。 ④根据上面的数据建立线性回归模型: t t t t y = b + b x + b x + u 0 1 1 2 2 ⑤比较以上两个模型的可决系数。 ⑥如果以上两个模型的结论不同,你将选择哪一个回归模型?为什么?

实验四多重共线性 【实验目的】 通过本实验,要求学生在理解计量经济模型中出现多重共线性的不良后果基础上,掌握 诊断多重共线性和修正多重共线性的若干方法:与实验三紧密联系起来,利用若干变量建立 多元回归模型过程中,要求学生能够独立分析和解决存在的多重共线性问题。 【实验内容】 一、我国财政收入影响因素分析(2-4-1.1) 二、我国旅游市场发展影响因素分析(2-4-2.f1) 三、经典案例:工业增加值与三大产业固定资产投资的联系(2-4-3.w1) 【实验步骤】 一、我国财或收入影响因素分析(2-4-1.wf1) 向题概述:建立中国1978-2003年的财政收入(CS,亿元)对农业增加值忆,亿元)、 工业增加值(GZ,亿元)、建筑业增加值JZZ,亿元)总人口(TPOP,万人)、最终消费(CM 亿元)和受灾面积(SZM,万公顷)的数最模型。 1.建立回归模型,估计模型的参数 Dependerntvarabiecs 9e2030 Std.Error +-Statistic Prob. 3191.09 3.695704 0.001 020 SZM -0.036836 0.018460-1.995382 0.060 08950 589782 E0 193.416 5141 Prob(F-statistic) 0.000000 图2-4-1估计回归模型的结果 在Equation Estimation窗口输入CS C NZ GZ JZZ RPOP CUM SZN,得到回归估计果
29 实验四 多重共线性 【实验目的】 通过本实验,要求学生在理解计量经济模型中出现多重共线性的不良后果基础上,掌握 诊断多重共线性和修正多重共线性的若干方法;与实验三紧密联系起来,利用若干变量建立 多元回归模型过程中,要求学生能够独立分析和解决存在的多重共线性问题。 【实验内容】 一、我国财政收入影响因素分析(2-4-1.wf1) 二、我国旅游市场发展影响因素分析(2-4-2.wf1) 三、经典案例:工业增加值与三大产业固定资产投资的联系(2-4-3.wf1) 【实验步骤】 一、我国财政收入影响因素分析(2-4-1.wf1) 问题概述:建立中国 1978-2003 年的财政收入(CS,亿元)对农业增加值(NZ,亿元)、 工业增加值(GZ,亿元)、建筑业增加值(JZZ,亿元) 总人口(TPOP,万人)、 最终消费(CUM, 亿元)和受灾面积(SZM,万公顷)的数量模型。 1.建立回归模型,估计模型的参数 图 2-4-1 估计回归模型的结果 在 Equation Estimation 窗口输入 CS C NZ GZ JZZ RPOP CUM SZM,得到回归估计果