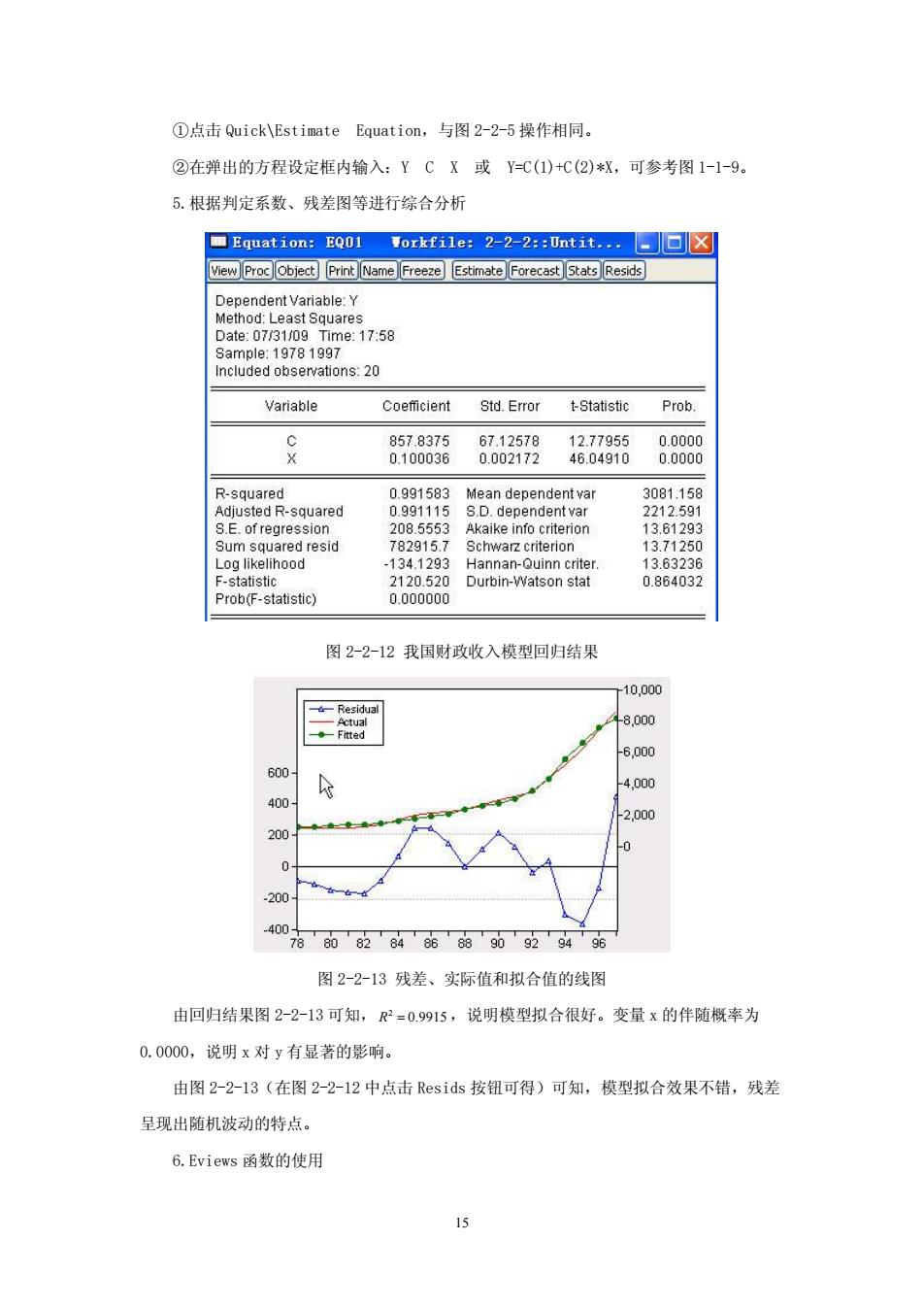
①点击Quick\Estin te Equation,与图2-2-5操作相同。 ②在弹出的方程设定框内输入:YCX或Y=C(1)+C(②)*X,可参考图1-1-9。 5.根据判定系数、残差图等进行综合分析 ▣Equation:EQ01 Workfi1e:2-2-2:0ntit,□▣☒ ew Proc object Print Name Freeze Estimate Forecast Stats Resids Dependent Variable:Y Coefficient Std.Error Statistic Prob. 870279 0.991583 0.991115 Enog03redresid 7929157 1371250 134.1293 Hannan 08623 Prob(F-staistic) 0.000000 图2-2-12我国财政收入模型回归结果 10,000 一R 8000 6,000 60 4.000 400 2,000 200 200 40为024的的0294的 图2-2-13残差、实际值和拟合值的线图 由回归结果图2-2-13可知,R=0.9915,说明模型拟合很好。变量x的伴随概率为 0.0000,说明x对y有显著的影响。 由图2-2-13(在图2-2-12中点击Resids按纽可得)可知,模型拟合效果不错,残差 呈现出随机波动的特点。 6.Eviews函数的使用
15 ①点击 Quick\Estimate Equation,与图 2-2-5 操作相同。 ②在弹出的方程设定框内输入:Y C X 或 Y=C(1)+C(2)*X,可参考图 1-1-9。 5.根据判定系数、残差图等进行综合分析 图 2-2-12 我国财政收入模型回归结果 图 2-2-13 残差、实际值和拟合值的线图 由回归结果图 2-2-13 可知, 2 R = 0.9915,说明模型拟合很好。变量 x 的伴随概率为 0.0000,说明 x 对 y 有显著的影响。 由图 2-2-13(在图 2-2-12 中点击 Resids 按钮可得)可知,模型拟合效果不错,残差 呈现出随机波动的特点。 6.Eviews 函数的使用

(1)常用函数(以@符号为起始符) ①序列描述统计函数:均值[@MEAN(]:相关系数[@CORO]:协方差[@COv0]等。 ②分布函数:标准正态分布[CNORM0]:t分布[&TDIST(x,v)]等。 ③分位数函数:t分位数[@QTDIST(p,)]:f分位数[@QFDIST(p,1,2)]等 ④回归统计函数(重点):回归参数标准差[@STDERRS(i)]:回归系数[@COEFS()①]:回 归标准差[@SE]:回归可决系数[eR2]:残差平方和[eSSR]等。 (2)用函数完成参数估计和预测区间的计算(在Eviews命令窗口内) series difx=-x-emean(x)‘建立x与其均值的离差序列 series dify=y-@mean(y) series difx2=difx*difx‘计算离差平方 seriesdifxdify=difx*dify EVievs 口orkf11e:2-2-2-(d:\我的文挡\2-2-2.f etiesdedtrdw 国998 图2-2-14序列的生成 在Eviews命令窗口中,输入以上命令,得到如图2-2-14所显示的序列。 EViews File Edit Obiect view Proc Quick Options Window Help MewProc object (Prnt]Save Detals+Show Fetch ore Delete Genr]Sample ae1978197388b Display Filter. 2=0.10003310849 图2-2-15参数的计算 scalar b2=esum(difxdify))/esum(difx2)‘计算回归系数 6
16 (1)常用函数(以@符号为起始符) ①序列描述统计函数:均值[@MEAN()];相关系数[@COR()];协方差[@COV()]等。 ②分布函数:标准正态分布[@CNORM()];t 分布[@TDIST(x,v)]等。 ③分位数函数:t 分位数[@QTDIST(p,v)];f 分位数[@QFDIST(p,v1,v2)]等。 ④回归统计函数(重点):回归参数标准差[@STDERRS(i)];回归系数[@COEFS(i)];回 归标准差[@SE];回归可决系数[@R2];残差平方和[@SSR]等。 (2)用函数完成参数估计和预测区间的计算(在 Eviews 命令窗口内) series difx=x-@mean(x) ‘建立 x 与其均值的离差序列 series dify=y-@mean(y) series difx2=difx*difx ‘计算离差平方 series difxdify=difx*dify 图 2-2-14 序列的生成 在 Eviews 命令窗口中,输入以上命令,得到如图 2-2-14 所显示的序列。 图 2-2-15 参数的计算 scalar b2=@sum(difxdify)/@sum(difx2) ‘计算回归系数
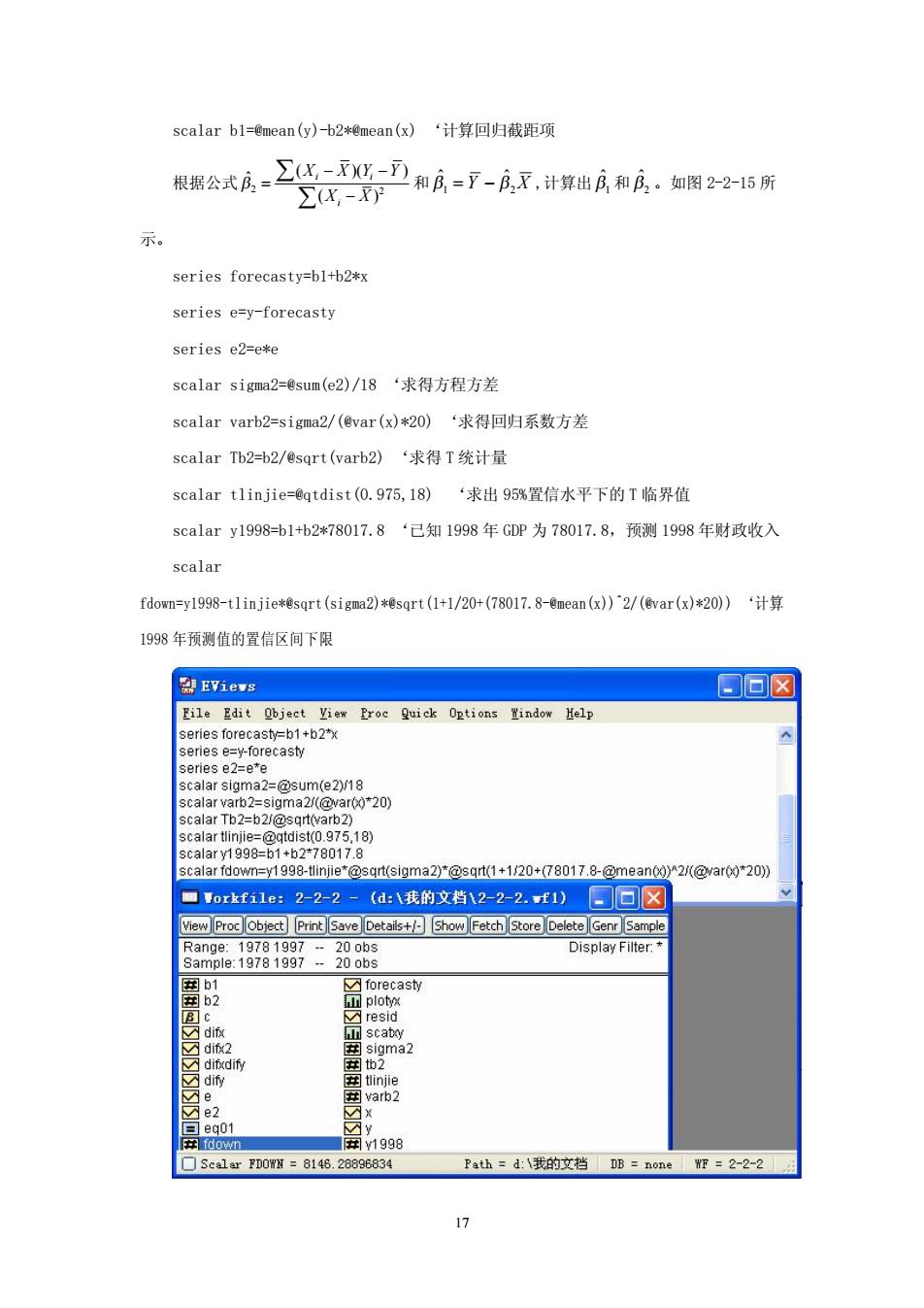
scalar b1=enean(y)-b2*mean(x)‘计算回归截距项 根据公式.2-和A=了-成了,计出月和A,实图2-15所 ∑X-T 示。 series forecasty=bl+b2*x series e=y-forecasty series e2=e*e scalar sigmaz2=sum(e2)/18‘求得方程方差 scalar varb2-sigma2/(evar(x)*20)‘求得回归系数方差 scalar Tb2=h2/@sqrt(varb2)‘求得T统计量 scalar t1 injie=@qtdist(0.975,18)‘求出95%管信水平下的T临界值 scalar y1998=b1+b2*78017.8‘已知1998年GDP为78017.8,预测1998年财政收入 scalar fdow=y1998-tlinjie*@sqrt(sigma2)*sqrt(1+1/20+(78017.8-@mean(x))"2/(@var(x)*20)) 1998年预测值的置信区间下限 EVievs ▣☒ File Edit Obiect view Proc Quick Options rindow Help eries forecast=b1+b2x ar sigma2-@sum e218 calar Tb2=b 1999= ar down= @sqr(sigma2)@sqr(1+1/+(780178-@mean()2/ ☐orkf11e:2-2-2-(d:\我的文挡\2-2-2.t1)▣区 3n1e.18781987二380 Display Fi ecast arb 司1998 ☐Sca1r10=8146.28836834 Path=d:1我的文档DB=none WF=2-2-2
17 scalar b1=@mean(y)-b2*@mean(x) ‘计算回归截距项 根据公式 2 2 ( )( ) ˆ ( ) i i i X X Y Y X X b - - = - å å 和 b ˆ 1 = Y - b ˆ 2X ,计算出 1 ˆb 和 2 ˆb 。如图 2-2-15 所 示。 series forecasty=b1+b2*x series e=y-forecasty series e2=e*e scalar sigma2=@sum(e2)/18 ‘求得方程方差 scalar varb2=sigma2/(@var(x)*20) ‘求得回归系数方差 scalar Tb2=b2/@sqrt(varb2) ‘求得 T 统计量 scalar tlinjie=@qtdist(0.975,18) ‘求出 95%置信水平下的 T 临界值 scalar y1998=b1+b2*78017.8 ‘已知 1998 年 GDP 为 78017.8,预测 1998 年财政收入 scalar fdown=y1998-tlinjie*@sqrt(sigma2)*@sqrt(1+1/20+(78017.8-@mean(x))^2/(@var(x)*20)) ‘计算 1998 年预测值的置信区间下限

图2-2-16置信区间的计算 求出1998年的预测值置信区间下限。如图2-2-16所示。根据公式: 乎产上+。可以得出193年的预测值宝合区闻下限为620, (3)使用回归统计函数获取回归过程的中间结果 在命令窗口键入Scalar a=SSR(将回归残差平方和的值赋给标量a):或者Scalar a=Stderrs()②(将第二个参数估计量的标准差赋给标量a),使用回归统计函数有利于更快 捷地计算其他相关的统计量。 【练习与作业】 1.开放作业(需上机前做好准备)。利用网络搜索有关计量经济学的网站、实证论文, 就感兴趣的某一问题及相关的实证论文,了解在实际经济背景下如何利用计量经济学软件建 立计量经济学模型的全过程。要求如下: (1)将查阅的资料录入生成工作文件:(2)用三种不同的操作方式完成回归分析,保 存回归结果:(3)对建立的模型进行经济理论检验、统计检验并对残差进行图形分析:(4) 写出回归分析报告,与论文的分析结果进行对比。 2.发生车祸次数与司机年龄有关吗? 作为交通安全研究的一部分,美国交通部采集了每1000个驾驶执照发生死亡事故的车 祸次数(number)和有驾驶执照的司机中21岁以下者所占比例(proportion)的数据,样本由 42个城市组成(数据见电子附件LX2-2.wf1)。 要求:(1)对这些数据做出数值的和图示的概述:(2)利用回归分析研究发生死亡事故 的车祸次数和有驾驶执照的司机中21岁以下者所占比例之间的关系,结合分析结果展开同 学间的讨论。(3)从你的分析中,你能得出什么结论或提出什么建议。 3.利用1988年9个工业国的名义利率(Y)与通货膨胀率(X)的数据(数据见电子附件 L2-3.w1),资料来源:原始数据来自国际货币基金组织出版的《国际金融统计》。分析下 列问题: (1)以利率为纵轴、通货膨胀率为横轴做图:(2)用0SL进行回归分析,写出求解步 骤:(3)如果实际利率不变,则名义利率与通货膨胀率的关系如何? 4.研究深圳市1990~2001年地方预算内财政收入(Y)与国内生产总值(风)的关系(数 据见电子附件LX2-4.wf1),资料来源:《深圳统计年鉴2002》,中国统计出版社。要求:
18 图 2-2-16 置信区间的计算 求出 1998 年的预测值置信区间下限。如图 2-2-16 所示。根据公式: å - - + + 2 2 1 ( ) ˆ 1 ˆ i f f x X X n Y ta s ,可以得出 1998 年的预测值置信区间下限为 8146.2890。 (3)使用回归统计函数获取回归过程的中间结果 在命令窗口键入 Scalar a=@SSR(将回归残差平方和的值赋给标量 a);或者 Scalar a=@Stderrs(2)(将第二个参数估计量的标准差赋给标量 a),使用回归统计函数有利于更快 捷地计算其他相关的统计量。 【练习与作业】 1.开放作业(需上机前做好准备)。利用网络搜索有关计量经济学的网站、实证论文, 就感兴趣的某一问题及相关的实证论文,了解在实际经济背景下如何利用计量经济学软件建 立计量经济学模型的全过程。要求如下: (1)将查阅的资料录入生成工作文件;(2)用三种不同的操作方式完成回归分析,保 存回归结果;(3)对建立的模型进行经济理论检验、统计检验并对残差进行图形分析;(4) 写出回归分析报告,与论文的分析结果进行对比。 2.发生车祸次数与司机年龄有关吗? 作为交通安全研究的一部分,美国交通部采集了每 1000 个驾驶执照发生死亡事故的车 祸次数(number)和有驾驶执照的司机中 21 岁以下者所占比例(proportion)的数据,样本由 42 个城市组成(数据见电子附件 LX2-2.wf1)。 要求:(1)对这些数据做出数值的和图示的概述;(2)利用回归分析研究发生死亡事故 的车祸次数和有驾驶执照的司机中 21 岁以下者所占比例之间的关系,结合分析结果展开同 学间的讨论。(3)从你的分析中,你能得出什么结论或提出什么建议。 3.利用 1988 年 9 个工业国的名义利率(Y)与通货膨胀率(X)的数据(数据见电子附件 LX2-3.wf1), 资料来源:原始数据来自国际货币基金组织出版的《国际金融统计》。分析下 列问题: (1)以利率为纵轴、通货膨胀率为横轴做图;(2)用 OSL 进行回归分析,写出求解步 骤;(3)如果实际利率不变,则名义利率与通货膨胀率的关系如何? 4.研究深圳市 1990~2001 年地方预算内财政收入(Y)与国内生产总值(X)的关系(数 据见电子附件 LX2-4.wf1),资料来源:《深圳统计年鉴 2002》,中国统计出版社。要求:

(1)建立深圳地方预算内财政收入对GDP的回归模型:(2)估计所建立模型的参数, 解释斜率系数的经济意义:(3)对回归结果进行检验,用命令方式计算参数估计量的置信区 间和预测的置信区间:(4)若是2005年年的国内生产总值为3600亿元,用命令方式确定 2005年财政收入的预测值和预测区间。 19
19 (1)建立深圳地方预算内财政收入对 GDP 的回归模型;(2)估计所建立模型的参数, 解释斜率系数的经济意义;(3)对回归结果进行检验,用命令方式计算参数估计量的置信区 间和预测的置信区间;(4)若是 2005 年年的国内生产总值为 3600 亿元,用命令方式确定 2005 年财政收入的预测值和预测区间