
最近邻法效果分析: /966 通过求无限样本下的平均条件错误率p(ex) 进行分析(略) 可证明,存在下列关系: P'≤P≤P2-eSP) 其中: P为无限样本数时的最近邻法的错误率 P*为贝叶斯错误率,即最小错误率,介于0~C] 之间。 (P(wx)=0时,P*=0;P(w/x)相等时,p=C-
最近邻法效果分析: * * * (2 ) 1 c P P P P c 可证明,存在下列关系: 通过求无限样本下的平均条件错误率p(e|x) 进行分析(略) 其中: 1 0 ~ c c P*为贝叶斯错误率,即最小错误率,介 于 之间。 (P(w/x)=0时, P* =0; P(w/x)相等时, P* c 1 ) c P为无限样本数时的最近邻法的错误率
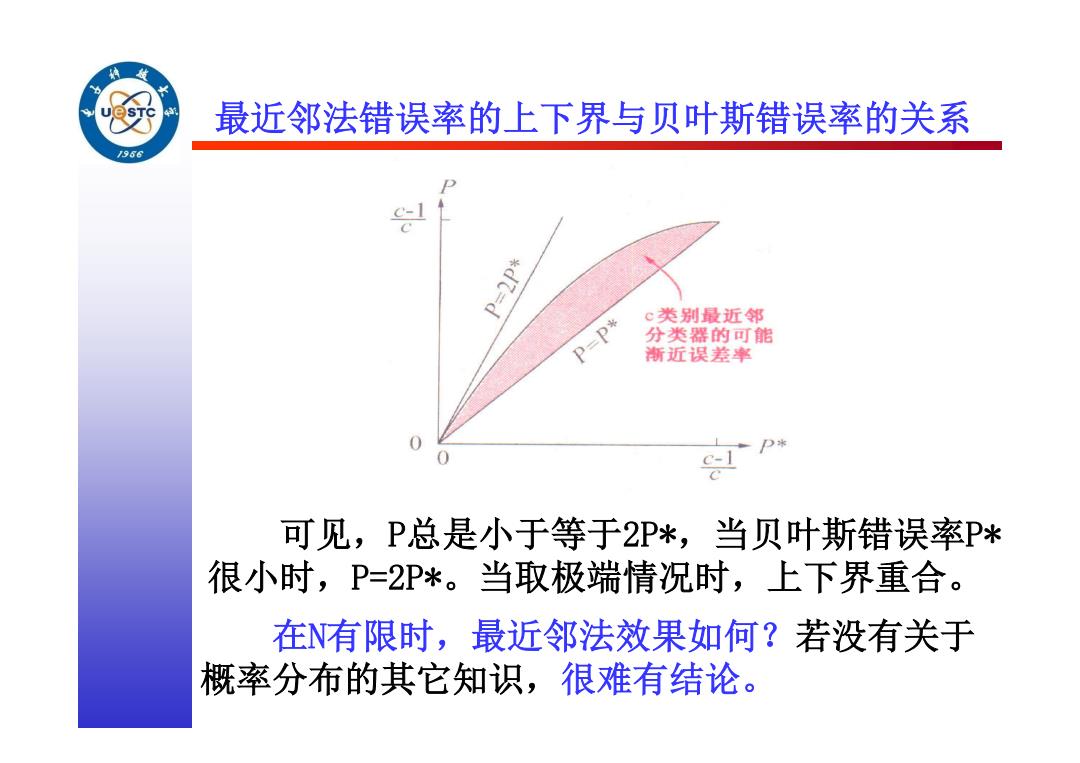
最近邻法错误率的上下界与贝叶斯错误率的关系 /96 P=2P* c类别最近邻 p=p* 分类器的可能 渐近误差率 c-1 可见,P总是小于等于2P*,当贝叶斯错误率P* 很小时,P=2P*。当取极端情况时,上下界重合。 在N有限时,最近邻法效果如何?若没有关于 概率分布的其它知识,很难有结论
可见,P总是小于等于2P*,当贝叶斯错误率P* 很小时,P=2P*。当取极端情况时,上下界重合。 最近邻法错误率的上下界与贝叶斯错误率的关系 在N有限时,最近邻法效果如何?若没有关于 概率分布的其它知识,很难有结论

K一近邻法 966 基本规则: 找出x的k个近邻,k个近邻中多数属于哪一类, 就把x归为哪一类。 x的k个近邻中,W,中有k个,w2中有k2个,,Wc 中有kc个,则 判别函数为:8,(x)=k,i=1,2,,c 决策规则: g,(x)=max k i=1,22,0 则决策x∈w
K—近邻法 g x k i c i i ( ) 1, 2,..., j i ( ) max 1, 2,..., i g x k i c j x w 基本规则: 判别函数为: 找出x的k个近邻,k个近邻中多数属于哪一类, 就把x归为哪一类。 决策规则: 则决策 x的k个近邻中,w1中有k1个,w2中有k2个,…,wc 中有kc个,则
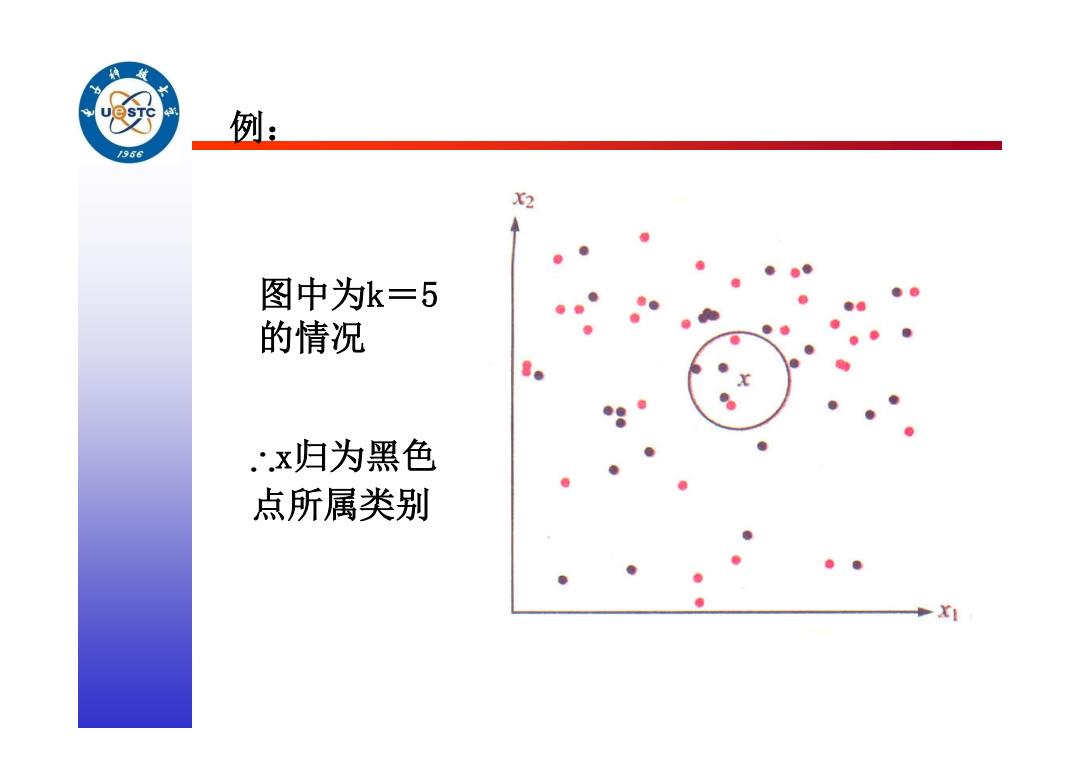
例: J966 X2 图中为k=5 的情况 8. x归为黑色 点所属类别
例: 图中为k=5 的情况 x归为黑色 点所属类别
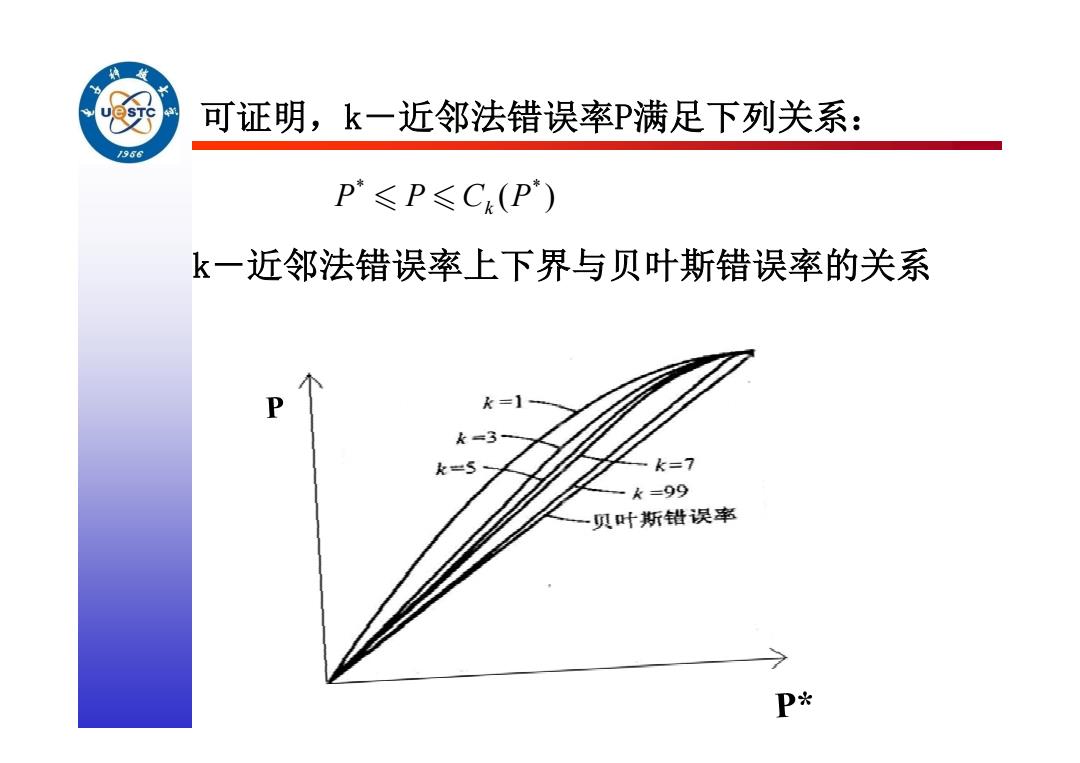
可证明,k一近邻法错误率P满足下列关系: 966 P≤P≤Ck(P) k一近邻法错误率上下界与贝叶斯错误率的关系 P k=】 k=3 k=5 k=7 k=99 贝叶斯错误率 P*
可证明,k-近邻法错误率P满足下列关系: * * ( ) P P C P k k-近邻法错误率上下界与贝叶斯错误率的关系