
p(Cil) p(C2) 1.0 0.0 reject region 图1.26:拒绝选项的例子。如果输入x使得两个后验概率分布中较大的那个概率分布小于或等于某个阈 值0,那么x会被拒绝识别。 形。注意,令0=1会使所有的样本都被拒绝,而如果有K个类别,那么令0<将会确保没有 样本被拒绝。因此被拒绝的样本比例由的值控制。 我们可以很容易地把拒绝准则推广到最小化期望损失的情形。那种情形下,我们已知一个损 失矩阵,这个矩阵考虑了拒绝决策所带来的损失。 1.5.4推断和决策 我们已经把分类问题划分成了两个阶段:推断(inference)阶段和决策(decision)阶段。在 推断阶段,我们使用训练数据学习(Ck|x)的模型。在接下来的决策阶段,我们使用这些后验 概率来进行最优的分类。另一种可能的方法是,同时解决两个问题,即简单地学习一个函数, 将输入c直接映射为决策。这样的函数被称为判别函数(discriminant function)。 事实上,我们可以区分出三种不同的方法来解决决策问题,这三种方法都已经在实际应用问 题中被使用。这三种方法按照复杂度降低的顺序给出: (a)首先对于每个类别Ck,独立地确定类条件密度p(x|Ck)。这是一个推断问题。然后,推 断先验类概率(Ck)。之后,使用贝叶斯定理 p(Cx)=p(C)p(Ck) (1.82) p(x) 求出后验类概率(Ck|x)。和往常一样,贝叶斯定理的分母可以用分子中出现的项表示,因为 p()=>p(ICx)p(Cx) (1.83) 等价地,我们可以直接对联合概率分布(x,C)建模,然后归一化,得到后验概率。得到后验概 率之后,我们可以使用决策论来确定每个新的输入x的类别。显式地或者隐式地对输入以及输 出进行建模的方法被称为生成式模型(generative model),因为通过取样,可以用来人工生成 出输入空间的数据点。 (b)首先解决确定后验类密度p(Ck|x)这一推断问题,接下来使用决策论来对新的输入x进行 分类。这种直接对后验概率建模的方法被称为判别式模型(discriminative models)。 (c)找到一个函数f(x),被称为判别函数。这个函数把每个输入x直接映射为类别标签。例 如,在二分类问题中,f()可能是一个二元的数值,f=0表示类别C1,f=1表示类别C2。这种 情况下,概率不起作用。 让我们考虑一下这三种方法的相对优势。方法()需要求解的东西最多,因为它涉及到寻找 在x和Ck上的联合概率分布。对于许多应用,x的维度很高,这会导致我们需要大量的训练数据 才能在合理的精度下确定类条件概率密度。注意,先验概率(Ck)经常能够根据训练数据集里的 每个类别的数据点所占的比例简单地估计出来。但是,方法()的一个优点是,它能够通过公式 (1.83)求出数据的边缘概率密度(x)。这对于检测模型中具有低概率的新数据点很有用,对于 36
x p(C1|x) p(C2|x) 0.0 1.0 θ reject region 图 1.26: 拒绝选项的例⼦。如果输⼊x使得两个后验概率分布中较⼤的那个概率分布⼩于或等于某个阈 值θ,那么x会被拒绝识别。 形。注意,令θ = 1会使所有的样本都被拒绝,⽽如果有K个类别,那么令θ < 1 K将会确保没有 样本被拒绝。因此被拒绝的样本⽐例由θ的值控制。 我们可以很容易地把拒绝准则推⼴到最⼩化期望损失的情形。那种情形下,我们已知⼀个损 失矩阵,这个矩阵考虑了拒绝决策所带来的损失。 1.5.4 推断和决策 我们已经把分类问题划分成了两个阶段:推断(inference)阶段和决策(decision)阶段。在 推断阶段,我们使⽤训练数据学习p(Ck | x)的模型。在接下来的决策阶段,我们使⽤这些后验 概率来进⾏最优的分类。另⼀种可能的⽅法是,同时解决两个问题,即简单地学习⼀个函数, 将输⼊x直接映射为决策。这样的函数被称为判别函数(discriminant function)。 事实上,我们可以区分出三种不同的⽅法来解决决策问题,这三种⽅法都已经在实际应⽤问 题中被使⽤。这三种⽅法按照复杂度降低的顺序给出: (a) ⾸先对于每个类别Ck,独⽴地确定类条件密度p(x | Ck)。这是⼀个推断问题。然后,推 断先验类概率p(Ck)。之后,使⽤贝叶斯定理 p(Ck | x) = p(x | Ck)p(Ck) p(x) (1.82) 求出后验类概率p(Ck | x)。和往常⼀样,贝叶斯定理的分母可以⽤分⼦中出现的项表⽰,因为 p(x) = ∑ k p(x | Ck)p(Ck) (1.83) 等价地,我们可以直接对联合概率分布p(x, Ck)建模,然后归⼀化,得到后验概率。得到后验概 率之后,我们可以使⽤决策论来确定每个新的输⼊x的类别。显式地或者隐式地对输⼊以及输 出进⾏建模的⽅法被称为⽣成式模型(generative model),因为通过取样,可以⽤来⼈⼯⽣成 出输⼊空间的数据点。 (b) ⾸先解决确定后验类密度p(Ck | x)这⼀推断问题,接下来使⽤决策论来对新的输⼊x进⾏ 分类。这种直接对后验概率建模的⽅法被称为判别式模型(discriminative models)。 (c) 找到⼀个函数f(x),被称为判别函数。这个函数把每个输⼊x直接映射为类别标签。例 如,在⼆分类问题中,f(·)可能是⼀个⼆元的数值,f = 0表⽰类别C1,f = 1表⽰类别C2。这种 情况下,概率不起作⽤。 让我们考虑⼀下这三种⽅法的相对优势。⽅法(a)需要求解的东西最多,因为它涉及到寻找 在x和Ck上的联合概率分布。对于许多应⽤,x的维度很⾼,这会导致我们需要⼤量的训练数据 才能在合理的精度下确定类条件概率密度。注意,先验概率p(Ck)经常能够根据训练数据集⾥的 每个类别的数据点所占的⽐例简单地估计出来。但是,⽅法(a)的⼀个优点是,它能够通过公式 (1.83)求出数据的边缘概率密度p(x)。这对于检测模型中具有低概率的新数据点很有⽤,对于 36
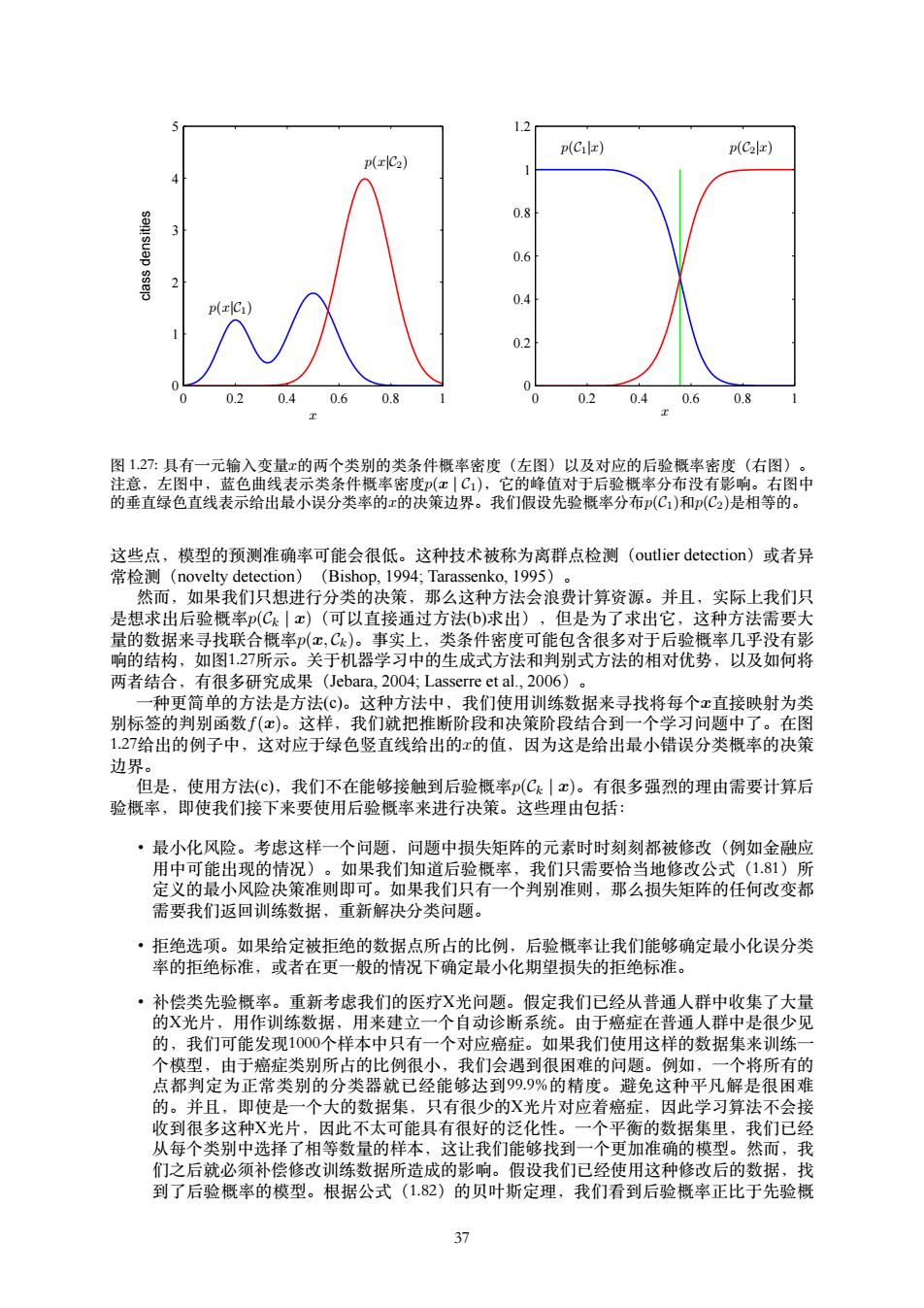
1.2 p(Cil) p(C2x) p(C2) 0.8 0.6 0.4 p( 0.2 0 0 0.2 0.40.6 0.8 0 0.20.40.6 0.8 图1.27:具有一元输入变量x的两个类别的类条件概率密度(左图)以及对应的后验概率密度(右图)。 注意,左图中,蓝色曲线表示类条件概率密度(x|C1),它的峰值对于后验概率分布没有影响。右图中 的垂直绿色直线表示给出最小误分类率的x的决策边界。我们假设先验概率分布p(C,)和(C2)是相等的。 这些点,模型的预测准确率可能会很低。这种技术被称为离群点检测(outlier detection)或者异 常检测(novelty detection)(Bishop,1994;Tarassenko,1995)。 然而,如果我们只想进行分类的决策,那么这种方法会浪费计算资源。并且,实际上我们只 是想求出后验概率(C|x)(可以直接通过方法(b)求出),但是为了求出它,这种方法需要大 量的数据来寻找联合概率(x,Ck)。事实上,类条件密度可能包含很多对于后验概率几乎没有影 响的结构,如图1.27所示。关于机器学习中的生成式方法和判别式方法的相对优势,以及如何将 两者结合,有很多研究成果(Jebara,2004;Lasserre et al,.2006)。 种更简单的方法是方法(©)。这种方法中,我们使用训练数据来寻找将每个x直接映射为类 别标签的判别函数f(x)。这样,我们就把推断阶段和决策阶段结合到一个学习问题中了。在图 1.27给出的例子中,这对应于绿色竖直线给出的x的值,因为这是给出最小错误分类概率的决策 边界。 但是,使用方法(c),我们不在能够接触到后验概率(Ck|c)。有很多强烈的理由需要计算后 验概率,即使我们接下来要使用后验概率来进行决策。这些理由包括: ·最小化风险。考虑这样一个问题,问题中损失矩阵的元素时时刻刻都被修改(例如金融应 用中可能出现的情况)。如果我们知道后验概率,我们只需要恰当地修改公式(1.81)所 定义的最小风险决策准则即可。如果我们只有一个判别准则,那么损失矩阵的任何改变都 需要我们返回训练数据,重新解决分类问题。 ·拒绝选项。如果给定被拒绝的数据点所占的比例,后验概率让我们能够确定最小化误分类 率的拒绝标准,或者在更一般的情况下确定最小化期望损失的拒绝标准。 ·补偿类先验概率。重新考虑我们的医疗X光问题。假定我们已经从普通人群中收集了大量 的X光片,用作训练数据,用来建立一个自动诊断系统。由于癌症在普通人群中是很少见 的,我们可能发现1000个样本中只有一个对应癌症。如果我们使用这样的数据集来训练一 个模型,由于癌症类别所占的比例很小,我们会遇到很困难的问题。例如,一个将所有的 点都判定为正常类别的分类器就已经能够达到999%的精度。避免这种平凡解是很困难 的。并且,即使是一个大的数据集,只有很少的X光片对应着癌症,因此学习算法不会接 收到很多这种X光片,因此不太可能具有很好的泛化性。一个平衡的数据集里,我们已经 从每个类别中选择了相等数量的样本,这让我们能够找到一个更加准确的模型。然而,我 们之后就必须补偿修改训练数据所造成的影响。假设我们已经使用这种修改后的数据,找 到了后验概率的模型。根据公式(1.82)的贝叶斯定理,我们看到后验概率正比于先验概 37
p(x|C1) p(x|C2) x class densities 0 0.2 0.4 0.6 0.8 1 0 1 2 3 4 5 x p(C1|x) p(C2|x) 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 1.2 图 1.27: 具有⼀元输⼊变量x的两个类别的类条件概率密度(左图)以及对应的后验概率密度(右图)。 注意,左图中,蓝⾊曲线表⽰类条件概率密度p(x | C1),它的峰值对于后验概率分布没有影响。右图中 的垂直绿⾊直线表⽰给出最⼩误分类率的x的决策边界。我们假设先验概率分布p(C1)和p(C2)是相等的。 这些点,模型的预测准确率可能会很低。这种技术被称为离群点检测(outlier detection)或者异 常检测(novelty detection)(Bishop, 1994; Tarassenko, 1995)。 然⽽,如果我们只想进⾏分类的决策,那么这种⽅法会浪费计算资源。并且,实际上我们只 是想求出后验概率p(Ck | x)(可以直接通过⽅法(b)求出),但是为了求出它,这种⽅法需要⼤ 量的数据来寻找联合概率p(x, Ck)。事实上,类条件密度可能包含很多对于后验概率⼏乎没有影 响的结构,如图1.27所⽰。关于机器学习中的⽣成式⽅法和判别式⽅法的相对优势,以及如何将 两者结合,有很多研究成果(Jebara, 2004; Lasserre et al., 2006)。 ⼀种更简单的⽅法是⽅法(c)。这种⽅法中,我们使⽤训练数据来寻找将每个x直接映射为类 别标签的判别函数f(x)。这样,我们就把推断阶段和决策阶段结合到⼀个学习问题中了。在图 1.27给出的例⼦中,这对应于绿⾊竖直线给出的x的值,因为这是给出最⼩错误分类概率的决策 边界。 但是,使⽤⽅法(c),我们不在能够接触到后验概率p(Ck | x)。有很多强烈的理由需要计算后 验概率,即使我们接下来要使⽤后验概率来进⾏决策。这些理由包括: • 最⼩化风险。考虑这样⼀个问题,问题中损失矩阵的元素时时刻刻都被修改(例如⾦融应 ⽤中可能出现的情况)。如果我们知道后验概率,我们只需要恰当地修改公式(1.81)所 定义的最⼩风险决策准则即可。如果我们只有⼀个判别准则,那么损失矩阵的任何改变都 需要我们返回训练数据,重新解决分类问题。 • 拒绝选项。如果给定被拒绝的数据点所占的⽐例,后验概率让我们能够确定最⼩化误分类 率的拒绝标准,或者在更⼀般的情况下确定最⼩化期望损失的拒绝标准。 • 补偿类先验概率。重新考虑我们的医疗X光问题。假定我们已经从普通⼈群中收集了⼤量 的X光⽚,⽤作训练数据,⽤来建⽴⼀个⾃动诊断系统。由于癌症在普通⼈群中是很少见 的,我们可能发现1000个样本中只有⼀个对应癌症。如果我们使⽤这样的数据集来训练⼀ 个模型,由于癌症类别所占的⽐例很⼩,我们会遇到很困难的问题。例如,⼀个将所有的 点都判定为正常类别的分类器就已经能够达到99.9%的精度。避免这种平凡解是很困难 的。并且,即使是⼀个⼤的数据集,只有很少的X光⽚对应着癌症,因此学习算法不会接 收到很多这种X光⽚,因此不太可能具有很好的泛化性。⼀个平衡的数据集⾥,我们已经 从每个类别中选择了相等数量的样本,这让我们能够找到⼀个更加准确的模型。然⽽,我 们之后就必须补偿修改训练数据所造成的影响。假设我们已经使⽤这种修改后的数据,找 到了后验概率的模型。根据公式(1.82)的贝叶斯定理,我们看到后验概率正⽐于先验概 37

率,而先验概率可以表示为每个类别的数据点所占的比例。因此我们可以把从人造的平衡 数据中得到的后验概率除以数据集里的类比例,再乘以我们想要应用模型的目标人群中类 别的比例即可。最后,我们需要归一化来保证新的后验概率之和等于1。注意,如果我们 直接学习一个判别函数而不确定后验概率,这个步骤就无法进行。 ·组合模型。对于复杂的应用来说,我们可能希望把问题分解成若干个小的子问题,每个子 问题都可以通过一个独立的模型解决。例如,在我们假想的医疗诊断问题中,我们可能有 来自血液检查的数据,以及X光片。我们不把所有的这种同样类型的信息集中到一个巨大 的输入空间中,而是建立一个系统来表示X光片而另一个系统来表示血液数据。这样做效 率更高。只要两个模型都给出类别的后验概率,我们就能够使用概率的规则系统化地结合 输出。完成这个目标的一个简单的方式是假设对于每个类别,X光片的输入的分布(记 作x1)和血液数据的输入的分布(记作xB)是独立的,因此 p(I,B Ck)=p(I Ck)p(B Ck) (1.84) 这是条件独立(conditional independence)的一个例子,因为当分布以类别Ck为条件时满 足独立性。同时给出X光片和血液数据,后验概率为 p(Ck 1,B)p(I,B Ck)p(Ck) p(ICk)p(B Ck)p(Ck) x p(C)p(C) (1.85) p(Ck) 因此我们需要求出类先验概率(C),这可以通过估计每个类别的数据点所占的比例很容 易地得到。之后我们需要对后验概率归一化,使得后验概率之和等于1。公式(1.84) 的独立性假设是朴素贝叶斯模型(naive Bayes model)的一个例子。注意,联合边缘分 布(x1,xB)在这个模型下通常不会被分解。在后续章节中,我们会看到如何不依赖公式 (1.84)的独立性假设来建立组合数据的模型。 1.5.5回归问题的损失函数 目前为止,我们以分类问题为例,讨论了决策论。我们现在考虑回归问题,例如之前讨论过 的曲线拟合问题。决策阶段包括对于每个输入x,选择一个对于t值的具体的估计(c)。假设这 样做之后,我们造成了一个损失L(t,(x)。平均损失(或者说期望损失)就是 EIL]= L(t,y(x))p(x,t)dx dt (1.86 回归问题中,损失函数的一个通常的选择是平方损失,定义为L(t,y(c)={y(c)-t}。这种情 况下,期望损失函数可以写成 L]=u()-t)2p(2,t)da dt (1.87 我们的目标是选择y(x)来最小化EL]。如果我们假设一个完全任意的函数y(x),我们能够形式 化地使用变分法求解: SEL y(x) =2 u()-thp(a,t)dt=0 (1.88) 求解y(x),使用概率的加和规则和乘积规则,我们得到 e)=∫p(r,t)dt tp(tx)dt =Etx (1.89) p(x) 这是在c的条件下t的条件均值,被称为回归函数(regression function)。结果如图1.28所示。 这个结果可以扩展到多个目标变量(用向量)的情形。这种情况下,最优解是条件均 值y(c)=Et[t|x。 38
率,⽽先验概率可以表⽰为每个类别的数据点所占的⽐例。因此我们可以把从⼈造的平衡 数据中得到的后验概率除以数据集⾥的类⽐例,再乘以我们想要应⽤模型的⽬标⼈群中类 别的⽐例即可。最后,我们需要归⼀化来保证新的后验概率之和等于1。注意,如果我们 直接学习⼀个判别函数⽽不确定后验概率,这个步骤就⽆法进⾏。 • 组合模型。对于复杂的应⽤来说,我们可能希望把问题分解成若⼲个⼩的⼦问题,每个⼦ 问题都可以通过⼀个独⽴的模型解决。例如,在我们假想的医疗诊断问题中,我们可能有 来⾃⾎液检查的数据,以及X光⽚。我们不把所有的这种同样类型的信息集中到⼀个巨⼤ 的输⼊空间中,⽽是建⽴⼀个系统来表⽰X光⽚⽽另⼀个系统来表⽰⾎液数据。这样做效 率更⾼。只要两个模型都给出类别的后验概率,我们就能够使⽤概率的规则系统化地结合 输出。完成这个⽬标的⼀个简单的⽅式是假设对于每个类别,X光⽚的输⼊的分布(记 作xI)和⾎液数据的输⼊的分布(记作xB)是独⽴的,因此 p(xI , xB | Ck) = p(xI | Ck)p(xB | Ck) (1.84) 这是条件独⽴(conditional independence)的⼀个例⼦,因为当分布以类别Ck为条件时满 ⾜独⽴性。同时给出X光⽚和⾎液数据,后验概率为 p(Ck | xI , xB) ∝ p(xI , xB | Ck)p(Ck) ∝ p(xI | Ck)p(xB | Ck)p(Ck) ∝ p(Ck | xI )p(Ck | xB) p(Ck) (1.85) 因此我们需要求出类先验概率p(Ck),这可以通过估计每个类别的数据点所占的⽐例很容 易地得到。之后我们需要对后验概率归⼀化,使得后验概率之和等于1。公式(1.84) 的独⽴性假设是朴素贝叶斯模型(naive Bayes model)的⼀个例⼦。注意,联合边缘分 布p(xI , xB)在这个模型下通常不会被分解。在后续章节中,我们会看到如何不依赖公式 (1.84)的独⽴性假设来建⽴组合数据的模型。 1.5.5 回归问题的损失函数 ⽬前为⽌,我们以分类问题为例,讨论了决策论。我们现在考虑回归问题,例如之前讨论过 的曲线拟合问题。决策阶段包括对于每个输⼊x,选择⼀个对于t值的具体的估计y(x)。假设这 样做之后,我们造成了⼀个损失L(t, y(x))。平均损失(或者说期望损失)就是 E[L] = ∫ ∫ L(t, y(x))p(x, t) dx dt (1.86) 回归问题中,损失函数的⼀个通常的选择是平⽅损失,定义为L(t, y(x)) = {y(x) − t} 2。这种情 况下,期望损失函数可以写成 E[L] = ∫ ∫ {y(x) − t} 2 p(x, t) dx dt (1.87) 我们的⽬标是选择y(x)来最⼩化E[L]。如果我们假设⼀个完全任意的函数y(x),我们能够形式 化地使⽤变分法求解: δE[L] δy(x) = 2 ∫ {y(x) − t}p(x, t) dt = 0 (1.88) 求解y(x),使⽤概率的加和规则和乘积规则,我们得到 y(x) = ∫ tp(x, t) dt p(x) = ∫ tp(t | x) dt = Et [t | x] (1.89) 这是在x的条件下t的条件均值,被称为回归函数(regression function)。结果如图1.28所⽰。 这 个 结 果 可 以 扩 展 到 多 个 ⽬ 标 变 量 (⽤ 向 量t) 的 情 形。 这 种 情 况 下, 最 优 解 是 条 件 均 值y(x) = Et [t | x]。 38

(x) y(xo) p(t zo) 工0 图1.28:最小化了期望平方损失的回归函数y(x)由条件概率分布(t|x)的均值给出。 我们也可以使用一种稍微不同的方式推导出这个结果,这也将透露出回归问题的本质。已经 知道了最优解是条件期望,我们可以把平方项按照下面的方式展开: y(z)-t)2=fy(x)-Et]+Etx]-t)2 =fy()-Elt x])2+2fy()-Et|x]Elt x]-th +{Et|x-t}2 其中,为了不让符号过于复杂,我们使用E[t|c来表示巴tx]。代入损失函数中,对进行积 分,我们看到交叉项消失,因而得到下面形式的损失函数 E[L]=/fy()-E[t l ])2p()da+/var[t xlp()da (1.90) 我们寻找的函数y(c)只出现在第一项中。当y(c)等于Et|x时第一项取得最小值,这时第一项 会被消去。这正是我们之前推导的结果,表明最优的最小平方预测由条件均值给出。第二项 是的分布的方差,在x上进行了平均。它表示目标数据内在的变化性,可以被看成噪声。由于 它与y(c)无关,因此它表示损失函数的不可减小的最小值。 与分类问题相同,我们可以确定合适的概率然后使用这些概率做出最优的决策,或者我们可 以建立直接决策的模型。实际上,我们可以区分出三种解决回归问题的方法,按照复杂度降低 的顺序,依次为: (a)首先解决确定联合概率密度(x,t)的推断问题。之后,计算条件概率密度p(t|x)。最 后,使用公式(1.89)积分,求出条件均值。 (b)首先解决确定条件概率密度(t川x)的推断问题。之后使用公式(1.89)计算条件均值。 (c)直接从训练数据中寻找一个回归函数y(x)。 这三种方法的相对优势和之前所述的分类问题的情形很相似。 平方损失函数不是回归问题中损失函数的唯一选择。实际上,有些情况下,平方损失函数会 导致非常差的结果,这时我们就需要更复杂的方法。这种情况的一个重要的例子就是条件分 布(t|c)有多个峰值,这在解决反演问题时经常出现。这里我们简要介绍一下平方损失函数的 一种推广,叫做闵可夫斯基损失函数(Minkowski loss),它的期望为 tl=f厂a-edd (1.91) 当q=2时,这个函数就变成了平方损失函数的期望。图1.29给出了不同q值下,函数|y-t9关 于y-t的图像。当q=2时,E[L的最小值是条件均值。当q=1时,E[L的最小值是条件中位 数。当q→O时,E[La]的最小值是条件众数。 1.6信息论 从概率论到决策论,本章中我们讨论了一系列的概念。这些概念将会组成本书后续章节中讨 论的基础。在本章的最后一节,我们要介绍信息论领域的一些概念。这些概念对于模式识别 39
t x0 x y(x0) y(x) p(t|x0) 图 1.28: 最⼩化了期望平⽅损失的回归函数y(x)由条件概率分布p(t | x)的均值给出。 我们也可以使⽤⼀种稍微不同的⽅式推导出这个结果,这也将透露出回归问题的本质。已经 知道了最优解是条件期望,我们可以把平⽅项按照下⾯的⽅式展开: {y(x) − t} 2 = {y(x) − E[t | x] + E[t | x] − t} 2 = {y(x) − E[t | x]} 2 + 2{y(x) − E[t | x]}{E[t | x] − t} + {E[t | x] − t} 2 其中,为了不让符号过于复杂,我们使⽤E[t | x]来表⽰Et [t | x]。代⼊损失函数中,对t进⾏积 分,我们看到交叉项消失,因⽽得到下⾯形式的损失函数 E[L] = ∫ {y(x) − E[t | x]} 2 p(x) dx + ∫ var[t | x]p(x) dx (1.90) 我们寻找的函数y(x)只出现在第⼀项中。当y(x)等于E[t | x]时第⼀项取得最⼩值,这时第⼀项 会被消去。这正是我们之前推导的结果,表明最优的最⼩平⽅预测由条件均值给出。第⼆项 是t的分布的⽅差,在x上进⾏了平均。它表⽰⽬标数据内在的变化性,可以被看成噪声。由于 它与y(x)⽆关,因此它表⽰损失函数的不可减⼩的最⼩值。 与分类问题相同,我们可以确定合适的概率然后使⽤这些概率做出最优的决策,或者我们可 以建⽴直接决策的模型。实际上,我们可以区分出三种解决回归问题的⽅法,按照复杂度降低 的顺序,依次为: (a) ⾸先解决确定联合概率密度p(x, t)的推断问题。之后,计算条件概率密度p(t | x)。最 后,使⽤公式(1.89)积分,求出条件均值。 (b) ⾸先解决确定条件概率密度p(t | x)的推断问题。之后使⽤公式(1.89)计算条件均值。 (c) 直接从训练数据中寻找⼀个回归函数y(x)。 这三种⽅法的相对优势和之前所述的分类问题的情形很相似。 平⽅损失函数不是回归问题中损失函数的唯⼀选择。实际上,有些情况下,平⽅损失函数会 导致⾮常差的结果,这时我们就需要更复杂的⽅法。这种情况的⼀个重要的例⼦就是条件分 布p(t | x)有多个峰值,这在解决反演问题时经常出现。这⾥我们简要介绍⼀下平⽅损失函数的 ⼀种推⼴,叫做闵可夫斯基损失函数(Minkowski loss),它的期望为 E[Lq] = ∫ ∫ |y(x) − t| q p(x, t) dx dt (1.91) 当q = 2时,这个函数就变成了平⽅损失函数的期望。图1.29给出了不同q值下,函数|y − t| q关 于y − t的图像。当q = 2时,E[Lq]的最⼩值是条件均值。当q = 1时,E[Lq]的最⼩值是条件中位 数。当q → 0时,E[Lq]的最⼩值是条件众数。 1.6 信息论 从概率论到决策论,本章中我们讨论了⼀系列的概念。这些概念将会组成本书后续章节中讨 论的基础。在本章的最后⼀节,我们要介绍信息论领域的⼀些概念。这些概念对于模式识别 39
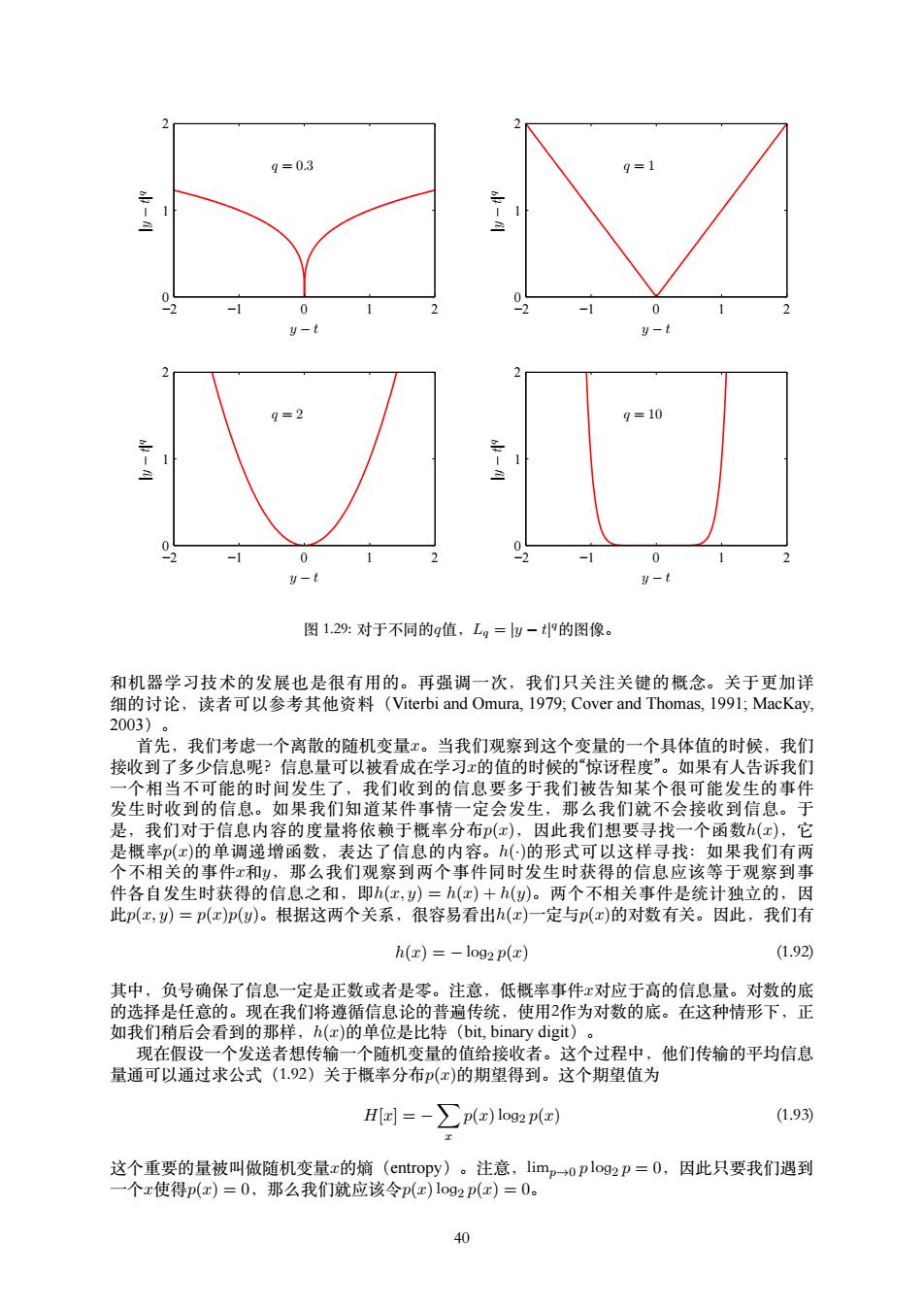
g=0.3 9=1 2 0 1 -2 -1 0 y-t y-t 9=10 0 U-t y-t 图129:对于不同的q值,Lg=y-t9的图像。 和机器学习技术的发展也是很有用的。再强调一次,我们只关注关键的概念。关于更加详 细的讨论,读者可以参考其他资料(Viterbi and Omura,1979,Cover and Thomas,199l;MacKay, 2003)。 首先,我们考虑一个离散的随机变量x。当我们观察到这个变量的一个具体值的时候,我们 接收到了多少信息呢?信息量可以被看成在学习x的值的时候的“惊讶程度”。如果有人告诉我们 一个相当不可能的时间发生了,我们收到的信息要多于我们被告知某个很可能发生的事件 发生时收到的信息。如果我们知道某件事情一定会发生,那么我们就不会接收到信息。于 是,我们对于信息内容的度量将依赖于概率分布(x),因此我们想要寻找一个函数(c),它 是概率(x)的单调递增函数,表达了信息的内容。()的形式可以这样寻找:如果我们有两 个不相关的事件x和y,那么我们观察到两个事件同时发生时获得的信息应该等于观察到事 件各自发生时获得的信息之和,即h(x,y)=h(x)+h(y)。两个不相关事件是统计独立的,因 此(x,)=p(x)p(g)。根据这两个关系,很容易看出h(x)一定与p(c)的对数有关。因此,我们有 h(x)=-10g2p(x) (1.92) 其中,负号确保了信息一定是正数或者是零。注意,低概率事件x对应于高的信息量。对数的底 的选择是任意的。现在我们将遵循信息论的普遍传统,使用2作为对数的底。在这种情形下,正 如我们稍后会看到的那样,h(x)的单位是比特(bit,binary digit)。 现在假设一个发送者想传输一个随机变量的值给接收者。这个过程中,他们传输的平均信息 量通可以通过求公式(1.92)关于概率分布(x)的期望得到。这个期望值为 Hl=-∑p(c)lo2px) (1.93) 这个重要的量被叫做随机变量x的熵(entropy)。注意,limp→o plog2p=0,因此只要我们遇到 一个x使得p(x)=0,那么我们就应该令p(x)log2p(x)=0。 40
y − t |y − t| q q = 0.3 −2 −1 0 1 2 0 1 2 y − t |y − t| q q = 1 −2 −1 0 1 2 0 1 2 y − t |y − t| q q = 2 −2 −1 0 1 2 0 1 2 y − t |y − t| q q = 10 −2 −1 0 1 2 0 1 2 图 1.29: 对于不同的q值,Lq = |y − t| q的图像。 和机器学习技术的发展也是很有⽤的。再强调⼀次,我们只关注关键的概念。关于更加详 细的讨论,读者可以参考其他资料(Viterbi and Omura, 1979; Cover and Thomas, 1991; MacKay, 2003)。 ⾸先,我们考虑⼀个离散的随机变量x。当我们观察到这个变量的⼀个具体值的时候,我们 接收到了多少信息呢?信息量可以被看成在学习x的值的时候的“惊讶程度”。如果有⼈告诉我们 ⼀个相当不可能的时间发⽣了,我们收到的信息要多于我们被告知某个很可能发⽣的事件 发⽣时收到的信息。如果我们知道某件事情⼀定会发⽣,那么我们就不会接收到信息。于 是,我们对于信息内容的度量将依赖于概率分布p(x),因此我们想要寻找⼀个函数h(x),它 是概率p(x)的单调递增函数,表达了信息的内容。h(·)的形式可以这样寻找:如果我们有两 个不相关的事件x和y,那么我们观察到两个事件同时发⽣时获得的信息应该等于观察到事 件各⾃发⽣时获得的信息之和,即h(x, y) = h(x) + h(y)。两个不相关事件是统计独⽴的,因 此p(x, y) = p(x)p(y)。根据这两个关系,很容易看出h(x)⼀定与p(x)的对数有关。因此,我们有 h(x) = − log2 p(x) (1.92) 其中,负号确保了信息⼀定是正数或者是零。注意,低概率事件x对应于⾼的信息量。对数的底 的选择是任意的。现在我们将遵循信息论的普遍传统,使⽤2作为对数的底。在这种情形下,正 如我们稍后会看到的那样,h(x)的单位是⽐特(bit, binary digit)。 现在假设⼀个发送者想传输⼀个随机变量的值给接收者。这个过程中,他们传输的平均信息 量通可以通过求公式(1.92)关于概率分布p(x)的期望得到。这个期望值为 H[x] = − ∑ x p(x)log2 p(x) (1.93) 这个重要的量被叫做随机变量x的熵(entropy)。注意,limp→0 p log2 p = 0,因此只要我们遇到 ⼀个x使得p(x) = 0,那么我们就应该令p(x)log2 p(x) = 0。 40