
其中,积分必须在整个x空间上进行。我们也可以考虑离散变量和连续变量相结合的联合概率 分布。 注意,如果x是一个离散变量,那么p(x)有时被叫做概率质量函数(probability mass function),因为它可以被看做集中在合法的x值处的“概率质量”的集合。 概率的加和规则和乘积规则以及贝叶斯规则,同样可以应用于概率密度函数的情形,也可以 应用于离散变量与连续变量相结合的情形。例如,如果x和y是两个实数变量,那么加和规则和 乘积规则的形式为 p(x)= p(x,y)dy (1.31) p(r,y)=p(y|x)p(x) (1.32) 形式化地证明连续变量的加和规则和乘积规则(Feller,1966)需要一个被称为测度论(measure thoy)的数学分支,不在本书的讨论范围内。然而,它的正确性可以非形式化地观察出来。把 每个实数变量除以区间的宽度△,然后考虑这些区间上的概率分布。取极限△→0,把求和转 化为积分,就得到了预期的结果。 1.2.2期望和协方差 涉及到概率的一个重要的操作是寻找函数的加权平均值。在概率分布(x)下,函数f(x)的平 均值被称为f(x)的期望(expectation),记作E[f]。对于一个离散变量,它的定义为 [f1=∑p()f) (1.33) 因此平均值根据x的不同值的相对概率加权。在连续变量的情形下,期望以对应的概率密度的积 分的形式表示 f1= p(x)f(x)dx (1.34) 两种情形下,如果我们给定有限数量的N个点,这些点满足某个概率分布或者概率密度函数, 那么期望可以通过求和的方式估计 N (1.35) n=1 在第11章讨论取样方法时,我们将会经常用到这个结果。当N→∞时,公式(1.35)的估计就 会变得精确。 有时,我们会考虑多变量函数的期望。这种情形下,我们可以使用下标来表明被平均的是哪 个变量,例如 E(f(x,y)] (1.36) 表示函数f(x,)关于x的分布的平均。注意,Ex[f(x,)]是y的一个函数。 我们也可以考虑关于一个条件分布的条件期望(conditional expectation),即 E.fl=∑p(e|)fe) (1.37 连续变量情形下的定义与此类似。 f(x)的方差(variance)被定义为 var[f]=E[(f()-E[f()])] (1.38) 它度量了f(x)在均值[f(x)]附近变化性的大小。把平方项展开,我们看到方差也可以写 成f(x)和f(x)2的期望的形式 var[f]E[f(z)2]-E[f(z)]2 (1.39) 21
其中,积分必须在整个x空间上进⾏。我们也可以考虑离散变量和连续变量相结合的联合概率 分布。 注 意, 如 果x是 ⼀ 个 离 散 变 量, 那 么p(x)有 时 被 叫 做 概 率 质 量 函 数 (probability mass function),因为它可以被看做集中在合法的x值处的“概率质量”的集合。 概率的加和规则和乘积规则以及贝叶斯规则,同样可以应⽤于概率密度函数的情形,也可以 应⽤于离散变量与连续变量相结合的情形。例如,如果x和y是两个实数变量,那么加和规则和 乘积规则的形式为 p(x) = ∫ p(x, y) dy (1.31) p(x, y) = p(y | x)p(x) (1.32) 形式化地证明连续变量的加和规则和乘积规则(Feller, 1966)需要⼀个被称为测度论(measure theory)的数学分⽀,不在本书的讨论范围内。然⽽,它的正确性可以⾮形式化地观察出来。把 每个实数变量除以区间的宽度∆,然后考虑这些区间上的概率分布。取极限∆ → 0,把求和转 化为积分,就得到了预期的结果。 1.2.2 期望和协⽅差 涉及到概率的⼀个重要的操作是寻找函数的加权平均值。在概率分布p(x)下,函数f(x)的平 均值被称为f(x)的期望(expectation),记作E[f]。对于⼀个离散变量,它的定义为 E[f] = ∑ x p(x)f(x) (1.33) 因此平均值根据x的不同值的相对概率加权。在连续变量的情形下,期望以对应的概率密度的积 分的形式表⽰ E[f] = ∫ p(x)f(x) dx (1.34) 两种情形下,如果我们给定有限数量的N个点,这些点满⾜某个概率分布或者概率密度函数, 那么期望可以通过求和的⽅式估计 E[f] ≃ 1 N ∑ N n=1 f(xn) (1.35) 在第11章讨论取样⽅法时,我们将会经常⽤到这个结果。当N → ∞时,公式(1.35)的估计就 会变得精确。 有时,我们会考虑多变量函数的期望。这种情形下,我们可以使⽤下标来表明被平均的是哪 个变量,例如 Ex[f(x, y)] (1.36) 表⽰函数f(x, y)关于x的分布的平均。注意,Ex[f(x, y)]是y的⼀个函数。 我们也可以考虑关于⼀个条件分布的条件期望(conditional expectation),即 Ex[f | y] = ∑ x p(x | y)f(x) (1.37) 连续变量情形下的定义与此类似。 f(x)的⽅差(variance)被定义为 var[f] = E[(f(x) − E[f(x)])2 ] (1.38) 它 度 量 了f(x)在 均 值E[f(x)]附 近 变 化 性 的 ⼤ ⼩。 把 平 ⽅ 项 展 开, 我 们 看 到 ⽅ 差 也 可 以 写 成f(x)和f(x) 2的期望的形式 var[f] = E[f(x) 2 ] − E[f(x)]2 (1.39) 21

特别地,我们可以考虑变量x自身的方差,它由下式给出: var[]E[x2]-E[z]2 (1.40) 对于两个随机变量x和y,协方差(covariance)被定义为 cov[,y]=Ez.y(ft-E[]Hy-Ely]]=Ez.y[xy]-E[x Ely] (1.41) 它表示在多大程度上x和y会共同变化。如果x和y相互独立,那么它们的协方差为0。 在两个随机向量x和y的情形下,协方差是一个矩阵 cov(c,y]=Ex.vlf-Elc]HyT-ElyT]}]Ea.vlcyT]-E(c]ElyT] (1.42 如果我们考虑向量c各个分量之间的协方差,那么我们可以将记号稍微简化一 下:cov[c]≡cov[r,c] 1.2.3贝叶斯概率 本章目前为止,我们根据随机重复事件的频率来考察概率。我们把这个叫做经典的 (classical)或者频率学家(frequentist)的关于概率的观点。现在我们转向更加通用的贝叶斯 (Bayesian)观点。这种观点中,频率提供了不确定性的一个定量化描述。 考虑一个不确定性事件,例如月球是否曾经处于围绕太阳的自己的轨道上,或者本世纪末北 极冰盖是否会消失。这些事件无法重复多次,因此我们无法像之前水果盒子那样定义概率。但 是,我们通常会有一些想法,例如,北极冰盖融化的速度等等。如果我们我们获得到了新鲜的 证据,例如人造卫星收集到了一些新的修正信息,我们可能就会修正我们对于冰盖融化速度的 观点。我们估计冰盖融化速度会影响我们采取的措施,例如我们会努力减少温室气体的排放。 在这样的情况下,我们可能希望能够定量地描述不确定性,并且根据少量新的证据对不确定性 进行精确的修改,对接下来将要采取的动作进行修改,或者对最终的决策进行修改。这可以通 过一种优雅的通用的贝叶斯概率观点来实现。 然而,在作出合理的推断时,如果我们想要尊重常识,那么使用概率论来表达不确定性不是 可选的,而是不可避免的。例如,Cox(1946)证明,如果用数值来表示置信的程度,那么编码 了这种置信度中符合常识的一组简单的公理能够唯一地推导出一组规则来操控置信的程度,这 组规则等价于概率的加和规则和乘积规则。这首次含糊地证明了概率论能够被当做布尔逻辑在 涉及到不确定性的问题时的扩展(Jaynes,2003)。许多其他学者也发表了不同的性质集合或者 公理集合,这些性质或公理是不确定性的度量应该满足的(Ramsey,.1931;Good,1950,Savage 1961;deFinetti,.1970,Lindley,1982)。在这些情形下,结果的数值量的行为精确地符合概率的 规则。因此把这些量看成(贝叶斯观点的)概率就很自然了。 在模式识别领域,对概率有一个更加通用的观点同样是很有帮助的。考虑1.1节讨论过的多 项式曲线拟合的例子。对于观察到的变量t这一随机值的概率,应用频率学家的观点似乎是很 合理的。然而,我们想针对模型参数心的合适选择进行强调和定量化。我们将会看到,从贝叶 斯的观点来看,我们能够使用概率论来描述模型参数(例如w)的不确定性,或者模型本身的 选择。 贝叶斯定理现在有了一个新的意义。回忆一下,在水果盒子的例子中,水果种类的观察提供 了相关的信息,改变了选择了红盒子的概率。在那个例子中,贝叶斯定理通过将观察到的数据 融合,来把先验概率转化为后验概率。正如我们将看到的,在我们对数量(例如多项式曲线拟 合例子中的参数心)进行推断时,我们可以采用一个类似的方法。在观察到数据之前,我们有 一些关于参数w的假设,这以先验概率p(w)的形式给出。观测数据D={t1,.,tN}的效果可以 通过条件概率(D|w)表达,我们将在1.2.5节看到这个如何被显式地表达出来。贝叶斯定理的形 式为 p(w|D)=P(DIw)p(w) (1.43) P(D) 它让我们能够通过后验概率(w|D),在观测到D之后估计心的不确定性。 22
特别地,我们可以考虑变量x⾃⾝的⽅差,它由下式给出: var[x] = E[x 2 ] − E[x] 2 (1.40) 对于两个随机变量x和y,协⽅差(covariance)被定义为 cov[x, y] = Ex,y[{x − E[x]}{y − E[y]}] = Ex,y[xy] − E[x]E[y] (1.41) 它表⽰在多⼤程度上x和y会共同变化。如果x和y相互独⽴,那么它们的协⽅差为0。 在两个随机向量x和y的情形下,协⽅差是⼀个矩阵 cov[x, y] = Ex,y[{x − E[x]}{y T − E[y T ]}] = Ex,y[xyT ] − E[x]E[y T ] (1.42) 如 果 我 们 考 虑 向 量x各 个 分 量 之 间 的 协 ⽅ 差, 那 么 我 们 可 以 将 记 号 稍 微 简 化 ⼀ 下:cov[x] ≡ cov[x, x] 1.2.3 贝叶斯概率 本 章 ⽬ 前 为 ⽌, 我 们 根 据 随 机 重 复 事 件 的 频 率 来 考 察 概 率。 我 们 把 这 个 叫 做 经 典 的 (classical)或者频率学家(frequentist)的关于概率的观点。现在我们转向更加通⽤的贝叶斯 (Bayesian)观点。这种观点中,频率提供了不确定性的⼀个定量化描述。 考虑⼀个不确定性事件,例如⽉球是否曾经处于围绕太阳的⾃⼰的轨道上,或者本世纪末北 极冰盖是否会消失。这些事件⽆法重复多次,因此我们⽆法像之前⽔果盒⼦那样定义概率。但 是,我们通常会有⼀些想法,例如,北极冰盖融化的速度等等。如果我们我们获得到了新鲜的 证据,例如⼈造卫星收集到了⼀些新的修正信息,我们可能就会修正我们对于冰盖融化速度的 观点。我们估计冰盖融化速度会影响我们采取的措施,例如我们会努⼒减少温室⽓体的排放。 在这样的情况下,我们可能希望能够定量地描述不确定性,并且根据少量新的证据对不确定性 进⾏精确的修改,对接下来将要采取的动作进⾏修改,或者对最终的决策进⾏修改。这可以通 过⼀种优雅的通⽤的贝叶斯概率观点来实现。 然⽽,在作出合理的推断时,如果我们想要尊重常识,那么使⽤概率论来表达不确定性不是 可选的,⽽是不可避免的。例如,Cox(1946)证明,如果⽤数值来表⽰置信的程度,那么编码 了这种置信度中符合常识的⼀组简单的公理能够唯⼀地推导出⼀组规则来操控置信的程度,这 组规则等价于概率的加和规则和乘积规则。这⾸次含糊地证明了概率论能够被当做布尔逻辑在 涉及到不确定性的问题时的扩展(Jaynes, 2003)。许多其他学者也发表了不同的性质集合或者 公理集合,这些性质或公理是不确定性的度量应该满⾜的(Ramsey, 1931; Good, 1950; Savage, 1961; deFinetti, 1970; Lindley, 1982)。在这些情形下,结果的数值量的⾏为精确地符合概率的 规则。因此把这些量看成(贝叶斯观点的)概率就很⾃然了。 在模式识别领域,对概率有⼀个更加通⽤的观点同样是很有帮助的。考虑1.1节讨论过的多 项式曲线拟合的例⼦。对于观察到的变量tn这⼀随机值的概率,应⽤频率学家的观点似乎是很 合理的。然⽽,我们想针对模型参数w的合适选择进⾏强调和定量化。我们将会看到,从贝叶 斯的观点来看,我们能够使⽤概率论来描述模型参数(例如w)的不确定性,或者模型本⾝的 选择。 贝叶斯定理现在有了⼀个新的意义。回忆⼀下,在⽔果盒⼦的例⼦中,⽔果种类的观察提供 了相关的信息,改变了选择了红盒⼦的概率。在那个例⼦中,贝叶斯定理通过将观察到的数据 融合,来把先验概率转化为后验概率。正如我们将看到的,在我们对数量(例如多项式曲线拟 合例⼦中的参数w)进⾏推断时,我们可以采⽤⼀个类似的⽅法。在观察到数据之前,我们有 ⼀些关于参数w的假设,这以先验概率p(w)的形式给出。观测数据D = {t1, . . . , tN }的效果可以 通过条件概率p(D | w)表达,我们将在1.2.5节看到这个如何被显式地表达出来。贝叶斯定理的形 式为 p(w | D) = p(D | w)p(w) p(D) (1.43) 它让我们能够通过后验概率p(w | D),在观测到D之后估计w的不确定性。 22

贝叶斯定理右侧的量(D|w)由观测数据集D来估计,可以被看成参数向量心的函数,被称 为似然函数(likelihood function)。它表达了在不同的参数向量w下,观测数据出现的可能性的 大小。注意,似然函数不是w的概率分布,并且它关于如的积分并不(一定)等于1。 给定似然函数的定义,我们可以用自然语言表述贝叶斯定理 posterior o likelihood x prior (1.44) 其中所有的量都可以看成心的函数。公式(1.43)的分母是一个归一化常数,确保了左侧的后验 概率分布是一个合理的概率密度,积分为1。实际上,对公式(1.43)的两侧关于0进行积分, 我们可以用后验概率分布和似然函数来表达贝叶斯定理的分母 P(D p(D w)p(w)dw (1.45) 在贝叶斯观点和频率学家观点中,似然函数(D|心)都起着重要的作用。然而,在两种观点 中,使用的方式有着本质的不同。在频率学家的观点中,心被认为是一个固定的参数,它的值 由某种形式的“估计”来确定,这个估计的误差通过考察可能的数据集D的概率分布来得到。相 反,从贝叶斯的观点来看,只有一个数据集D(即实际观测到的数据集),参数的不确定性通 过如的概率分布来表达。 频率学家广泛使用的一个估计是最大似然(maximum likelihood)估计,其中w的值是使似 然函数(D|)达到最大值的心值。这对应于选择使观察到的数据集出现概率最大的w的值。在 机器学习的文献中,似然函数的负对数被叫做误差函数(error function)。由于负对数是单调递 减的函数,最大化似然函数等价于最小化误差函数。 一种决定频率学家的误差的方法是自助法(bootstrap)(Efon,1979,Hastie et al.,2001)。 这种方法中,多个数据集使用下面的方式创造。假设我们的原始数据集由N个数据 点X={工1,,cw}组成。我们可以通过随机从X中抽取N个点的方式,创造一个新的数据 集XB。抽取时可以有重复,因此某些X中的数据点可能在XB中有重复,而其他的在X中的点 会在XB中缺失。这个过程可以重复L词,生成L个数据集,每个数据集的大小都是N,每个数 据集是通过对袁术数据集X采样得到的。参数估计的统计准确性之后就可以通过考察不同的自 助数据集之间的预测的变化性来进行评估。 贝叶斯观点的一个优点是对先验概率的包含是很自然的事情。例如,假定投掷一枚普通的硬 币3次,每次都是正面朝上。一个经典的最大似然模型在估计硬币正面朝上的概率时,结果会是 1,表示所有未来的投掷都会是正面朝上!相反,一个带有任意的合理的先验的贝叶斯的方法将 不会得出这么极端的结论。 关于频率学家的观点和贝叶斯的观点的相对优势有很多争论。事实上并没有纯粹的频率学家 观点或者贝叶斯的观点。例如,针对贝叶斯方法的一种广泛的批评就是先验概率的选择通常是 为了计算的方便而不是为了反映出任何先验的知识。某些人甚至把贝叶斯观点中结论对于先验 选择的依赖性的本质看成困难的来源。减少对于先验的依赖性是所谓无信息(noninformative) 先验的一个研究动机。然而,这会导致比较不同模型时的困难,并且实际上当先验选择不好的 时候,贝叶斯方法有很大的可能性会给出错误的结果。频率学家估计方法在一定程度上避免了 这一问题,并且例如交叉验证的技术在模型比较等方面也很有用。 本书着重强调贝叶斯观点,这反映出过去几年贝叶斯方法在实际应用中重要性的逐渐增长。 本书也会在必要的时候讨论有用的频率学家观点下的概念。 虽然贝叶斯的框架起源于18世纪,但是贝叶斯方法的实际应用在很长时间内都被执行完整的 贝叶斯步骤的困难性所限制,尤其是需要在整个参数空间求和或者求积分,这在做预测或者比 较不同的模型时必须进行。取样方法的发展,例如马尔科夫链蒙特卡罗(在第11章讨论),以 及计算机速度和存储容量的巨大提升,打开了在相当多的问题中使用贝叶斯技术的大门。蒙特 卡罗方法非常灵活,可以应用于许多种类的模型。然而,它们在计算上很复杂,主要应用于小 规模问题。 最近,许多高效的判别式方法被提出来,例如变种贝叶斯(variational Bayes)和期望传播 (expectation propagation)。这些提供了一种可选的补充的取样方法,让贝叶斯方法能够应用 于大规模的应用中(Blei et al.,2003)。 23
贝叶斯定理右侧的量p(D | w)由观测数据集D来估计,可以被看成参数向量w的函数,被称 为似然函数(likelihood function)。它表达了在不同的参数向量w下,观测数据出现的可能性的 ⼤⼩。注意,似然函数不是w的概率分布,并且它关于w的积分并不(⼀定)等于1。 给定似然函数的定义,我们可以⽤⾃然语⾔表述贝叶斯定理 posterior ∝ likelihood × prior (1.44) 其中所有的量都可以看成w的函数。公式(1.43)的分母是⼀个归⼀化常数,确保了左侧的后验 概率分布是⼀个合理的概率密度,积分为1。实际上,对公式(1.43)的两侧关于w进⾏积分, 我们可以⽤后验概率分布和似然函数来表达贝叶斯定理的分母 p(D) = ∫ p(D | w)p(w) dw (1.45) 在贝叶斯观点和频率学家观点中,似然函数p(D | w)都起着重要的作⽤。然⽽,在两种观点 中,使⽤的⽅式有着本质的不同。在频率学家的观点中,w被认为是⼀个固定的参数,它的值 由某种形式的“估计”来确定,这个估计的误差通过考察可能的数据集D的概率分布来得到。相 反,从贝叶斯的观点来看,只有⼀个数据集D(即实际观测到的数据集),参数的不确定性通 过w的概率分布来表达。 频率学家⼴泛使⽤的⼀个估计是最⼤似然(maximum likelihood)估计,其中w的值是使似 然函数p(D | w)达到最⼤值的w值。这对应于选择使观察到的数据集出现概率最⼤的w的值。在 机器学习的⽂献中,似然函数的负对数被叫做误差函数(error function)。由于负对数是单调递 减的函数,最⼤化似然函数等价于最⼩化误差函数。 ⼀种决定频率学家的误差的⽅法是⾃助法(bootstrap)(Efron, 1979; Hastie et al., 2001)。 这 种 ⽅ 法 中, 多 个 数 据 集 使 ⽤ 下 ⾯ 的 ⽅ 式 创 造。 假 设 我 们 的 原 始 数 据 集 由N个 数 据 点X = {x1, . . . , xN }组成。我们可以通过随机从X中抽取N个点的⽅式,创造⼀个新的数据 集XB。抽取时可以有重复,因此某些X中的数据点可能在XB中有重复,⽽其他的在X中的点 会在XB中缺失。这个过程可以重复L词,⽣成L个数据集,每个数据集的⼤⼩都是N,每个数 据集是通过对袁术数据集X采样得到的。参数估计的统计准确性之后就可以通过考察不同的⾃ 助数据集之间的预测的变化性来进⾏评估。 贝叶斯观点的⼀个优点是对先验概率的包含是很⾃然的事情。例如,假定投掷⼀枚普通的硬 币3次,每次都是正⾯朝上。⼀个经典的最⼤似然模型在估计硬币正⾯朝上的概率时,结果会是 1,表⽰所有未来的投掷都会是正⾯朝上!相反,⼀个带有任意的合理的先验的贝叶斯的⽅法将 不会得出这么极端的结论。 关于频率学家的观点和贝叶斯的观点的相对优势有很多争论。事实上并没有纯粹的频率学家 观点或者贝叶斯的观点。例如,针对贝叶斯⽅法的⼀种⼴泛的批评就是先验概率的选择通常是 为了计算的⽅便⽽不是为了反映出任何先验的知识。某些⼈甚⾄把贝叶斯观点中结论对于先验 选择的依赖性的本质看成困难的来源。减少对于先验的依赖性是所谓⽆信息(noninformative) 先验的⼀个研究动机。然⽽,这会导致⽐较不同模型时的困难,并且实际上当先验选择不好的 时候,贝叶斯⽅法有很⼤的可能性会给出错误的结果。频率学家估计⽅法在⼀定程度上避免了 这⼀问题,并且例如交叉验证的技术在模型⽐较等⽅⾯也很有⽤。 本书着重强调贝叶斯观点,这反映出过去⼏年贝叶斯⽅法在实际应⽤中重要性的逐渐增长。 本书也会在必要的时候讨论有⽤的频率学家观点下的概念。 虽然贝叶斯的框架起源于18世纪,但是贝叶斯⽅法的实际应⽤在很长时间内都被执⾏完整的 贝叶斯步骤的困难性所限制,尤其是需要在整个参数空间求和或者求积分,这在做预测或者⽐ 较不同的模型时必须进⾏。取样⽅法的发展,例如马尔科夫链蒙特卡罗(在第11章讨论),以 及计算机速度和存储容量的巨⼤提升,打开了在相当多的问题中使⽤贝叶斯技术的⼤门。蒙特 卡罗⽅法⾮常灵活,可以应⽤于许多种类的模型。然⽽,它们在计算上很复杂,主要应⽤于⼩ 规模问题。 最近,许多⾼效的判别式⽅法被提出来,例如变种贝叶斯(variational Bayes)和期望传播 (expectation propagation)。这些提供了⼀种可选的补充的取样⽅法,让贝叶斯⽅法能够应⽤ 于⼤规模的应⽤中(Blei et al., 2003)。 23
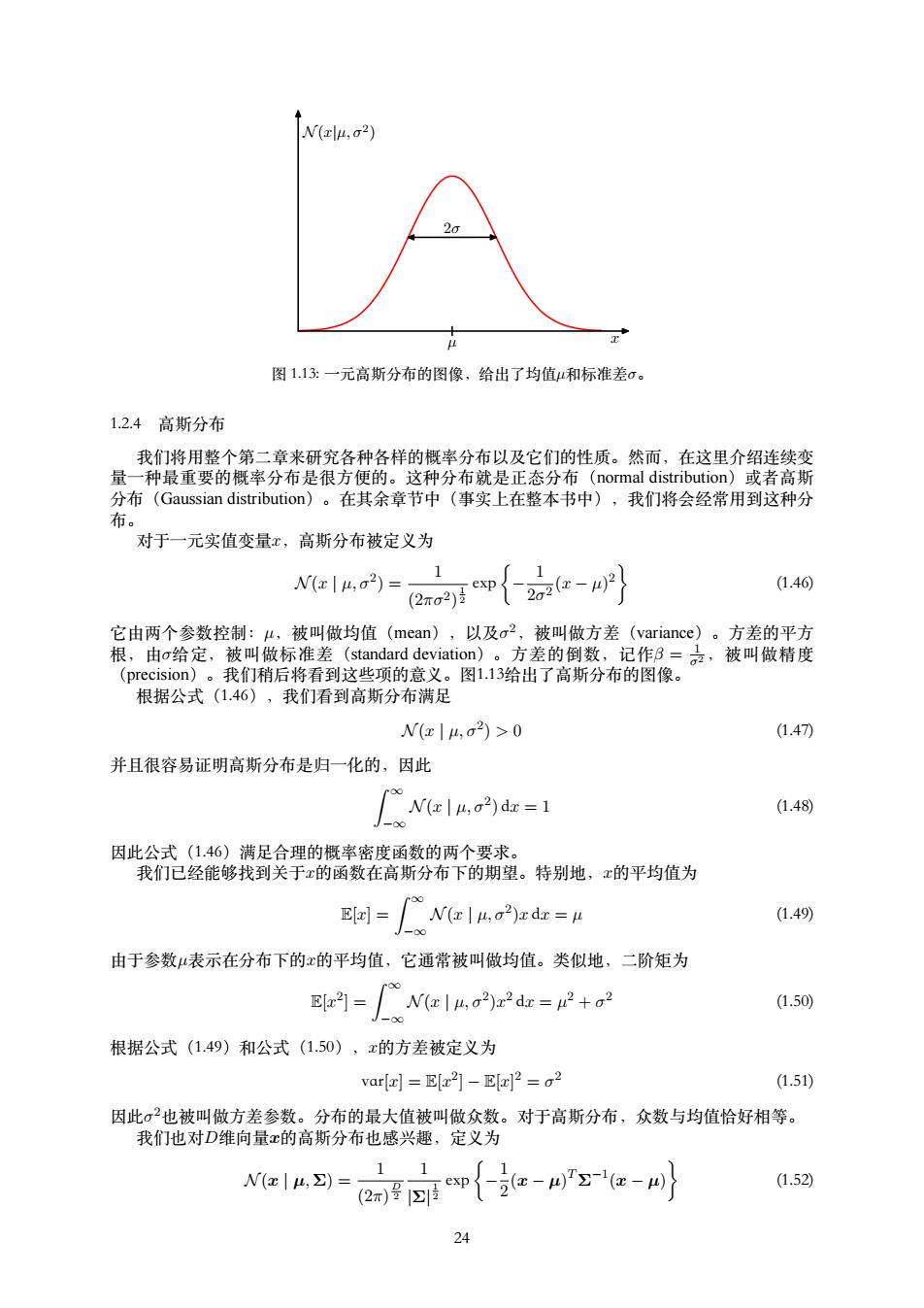
N(xμ,σ2) 20 图1.13:一元高斯分布的图像,给出了均值和标准差σ。 1.2.4高斯分布 我们将用整个第二章来研究各种各样的概率分布以及它们的性质。然而,在这里介绍连续变 量一种最重要的概率分布是很方便的。这种分布就是正态分布(normal distribution)或者高斯 分布(Gaussian distribution)。在其余章节中(事实上在整本书中),我们将会经常用到这种分 布。 对于一元实值变量x,高斯分布被定义为 N(xI4,2)= 1 1 (2xa2 cxp 2o2(x-四2 (1.46 它由两个参数控制:4,被叫做均值(mean),以及o2,被叫做方差(variance)。方差的平方 根,由o给定,被叫做标准差(standard deviation)。方差的倒数,记作B=亭,被叫做精度 (precision)。我们稍后将看到这些项的意义。图1.13给出了高斯分布的图像。 根据公式(1.46),我们看到高斯分布满足 W(x|4,o)>0 (1.47) 并且很容易证明高斯分布是归一化的,因此 N(al ,2)dz=1 (1.48) J-0 因此公式(1.46)满足合理的概率密度函数的两个要求。 我们已经能够找到关于x的函数在高斯分布下的期望。特别地,x的平均值为 Elx]= N(x|u,o2)xdx =p (1.49) 由于参数μ表示在分布下的x的平均值,它通常被叫做均值。类似地,二阶矩为 p的=Ne1A9rr=2+oe (1.50 根据公式(1.49)和公式(1.50),x的方差被定义为 var[]E[a2]-El]2 =o2 (1.51) 因此σ2也被叫做方差参数。分布的最大值被叫做众数。对于高斯分布,众数与均值恰好相等。 我们也对D维向量x的高斯分布也感兴趣,定义为 1 1 N(x|4,)= (1.52 24
N (x|µ, σ2 ) x 2σ µ 图 1.13: ⼀元⾼斯分布的图像,给出了均值µ和标准差σ。 1.2.4 ⾼斯分布 我们将⽤整个第⼆章来研究各种各样的概率分布以及它们的性质。然⽽,在这⾥介绍连续变 量⼀种最重要的概率分布是很⽅便的。这种分布就是正态分布(normal distribution)或者⾼斯 分布(Gaussian distribution)。在其余章节中(事实上在整本书中),我们将会经常⽤到这种分 布。 对于⼀元实值变量x,⾼斯分布被定义为 N (x | µ, σ2 ) = 1 (2πσ2) 1 2 exp { − 1 2σ 2 (x − µ) 2 } (1.46) 它由两个参数控制:µ,被叫做均值(mean),以及σ 2,被叫做⽅差(variance)。⽅差的平⽅ 根,由σ给定,被叫做标准差(standard deviation)。⽅差的倒数,记作β = 1 σ2,被叫做精度 (precision)。我们稍后将看到这些项的意义。图1.13给出了⾼斯分布的图像。 根据公式(1.46),我们看到⾼斯分布满⾜ N (x | µ, σ2 ) > 0 (1.47) 并且很容易证明⾼斯分布是归⼀化的,因此 ∫ ∞ −∞ N (x | µ, σ2 ) dx = 1 (1.48) 因此公式(1.46)满⾜合理的概率密度函数的两个要求。 我们已经能够找到关于x的函数在⾼斯分布下的期望。特别地,x的平均值为 E[x] = ∫ ∞ −∞ N (x | µ, σ2 )x dx = µ (1.49) 由于参数µ表⽰在分布下的x的平均值,它通常被叫做均值。类似地,⼆阶矩为 E[x 2 ] = ∫ ∞ −∞ N (x | µ, σ2 )x 2 dx = µ 2 + σ 2 (1.50) 根据公式(1.49)和公式(1.50),x的⽅差被定义为 var[x] = E[x 2 ] − E[x] 2 = σ 2 (1.51) 因此σ 2也被叫做⽅差参数。分布的最⼤值被叫做众数。对于⾼斯分布,众数与均值恰好相等。 我们也对D维向量x的⾼斯分布也感兴趣,定义为 N (x | µ, Σ) = 1 (2π) D 2 1 |Σ| 1 2 exp { − 1 2 (x − µ) T Σ−1 (x − µ) } (1.52) 24
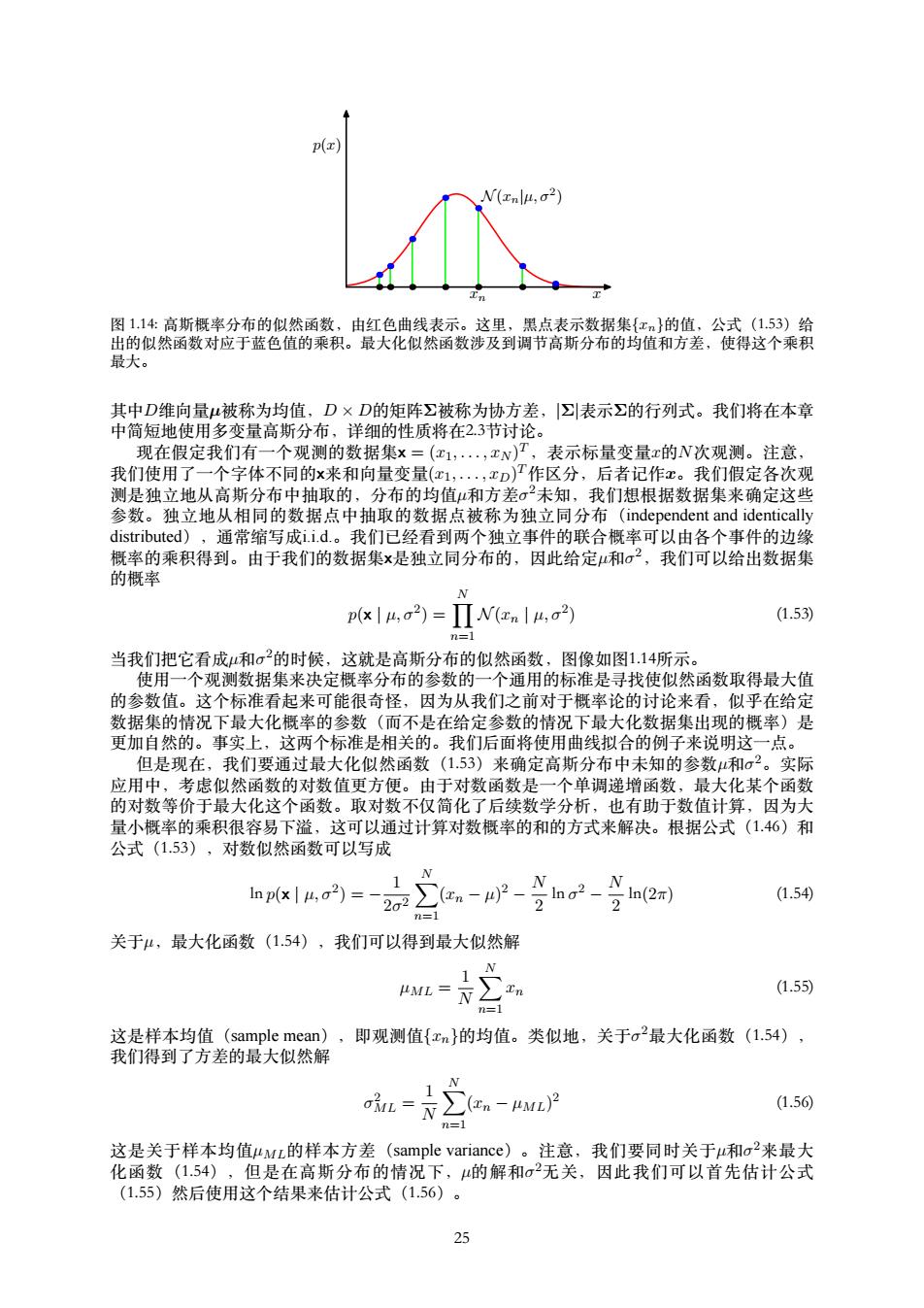
p(x) N(Inlu,o2) 图1.14:高斯概率分布的似然函数,由红色曲线表示。这里,黑点表示数据集{x}的值,公式(1.53)给 出的似然函数对应于蓝色值的乘积。最大化似然函数涉及到调节高斯分布的均值和方差,使得这个乘积 最大。 其中D维向量μ被称为均值,D×D的矩阵∑被称为协方差,表示∑的行列式。我们将在本章 中简短地使用多变量高斯分布,详细的性质将在23节讨论。 现在假定我们有一个观测的数据集x=(c1,·,xN)T,表示标量变量x的N次观测。注意, 我们使用了一个字体不同的x来和向量变量(x1,.,xD)T作区分,后者记作x。我们假定各次观 测是独立地从高斯分布中抽取的,分布的均值和方差σ2未知,我们想根据数据集来确定这些 参数。独立地从相同的数据点中抽取的数据点被称为独立同分布(independent and identically distributed),通常缩写成ii.d.。我们已经看到两个独立事件的联合概率可以由各个事件的边缘 概率的乘积得到。由于我们的数据集x是独立同分布的,因此给定和σ2,我们可以给出数据集 的概率 N px|h,o2)=ΠNenI4,a2) (1.53) n=1 当我们把它看成和σ的时候,这就是高斯分布的似然函数,图像如图1.14所示。 使用一个观测数据集来决定概率分布的参数的一个通用的标准是寻找使似然函数取得最大值 的参数值。这个标准看起来可能很奇怪,因为从我们之前对于概率论的讨论来看,似乎在给定 数据集的情况下最大化概率的参数(而不是在给定参数的情况下最大化数据集出现的概率)是 更加自然的。事实上,这两个标准是相关的。我们后面将使用曲线拟合的例子来说明这一点。 但是现在,我们要通过最大化似然函数(1.53)来确定高斯分布中未知的参数和σ2。实际 应用中,考虑似然函数的对数值更方便。由于对数函数是一个单调递增函数,最大化某个函数 的对数等价于最大化这个函数。取对数不仅简化了后续数学分析,也有助于数值计算,因为大 量小概率的乘积很容易下溢,这可以通过计算对数概率的和的方式来解决。根据公式(1.46)和 公式(1.53),对数似然函数可以写成 lnp(x|4,σ2)= 2o2 n-4)2、 2o2、 2n(2r) (1.54) 关于4,最大化函数(1.54),我们可以得到最大似然解 μML (1.55) m=1 这是样本均值(sample mean),即观测值{xn}的均值。类似地,关于o最大化函数(1.54), 我们得到了方差的最大似然解 ∑(n-4ML)2 (1.56) n=1 这是关于样本均值4ML的样本方差(sample variance)。注意,我们要同时关于u和a来最大 化函数(1.54),但是在高斯分布的情况下,的解和σ2无关,因此我们可以首先估计公式 (1.55)然后使用这个结果来估计公式(1.56)。 25
x p(x) xn N (xn|µ, σ2 ) 图 1.14: ⾼斯概率分布的似然函数,由红⾊曲线表⽰。这⾥,⿊点表⽰数据集{xn}的值,公式(1.53)给 出的似然函数对应于蓝⾊值的乘积。最⼤化似然函数涉及到调节⾼斯分布的均值和⽅差,使得这个乘积 最⼤。 其中D维向量µ被称为均值,D × D的矩阵Σ被称为协⽅差,|Σ|表⽰Σ的⾏列式。我们将在本章 中简短地使⽤多变量⾼斯分布,详细的性质将在2.3节讨论。 现在假定我们有⼀个观测的数据集x = (x1, . . . , xN ) T,表⽰标量变量x的N次观测。注意, 我们使⽤了⼀个字体不同的x来和向量变量(x1, . . . , xD) T作区分,后者记作x。我们假定各次观 测是独⽴地从⾼斯分布中抽取的,分布的均值µ和⽅差σ 2未知,我们想根据数据集来确定这些 参数。独⽴地从相同的数据点中抽取的数据点被称为独⽴同分布(independent and identically distributed),通常缩写成i.i.d.。我们已经看到两个独⽴事件的联合概率可以由各个事件的边缘 概率的乘积得到。由于我们的数据集x是独⽴同分布的,因此给定µ和σ 2,我们可以给出数据集 的概率 p(x | µ, σ2 ) = ∏ N n=1 N (xn | µ, σ2 ) (1.53) 当我们把它看成µ和σ 2的时候,这就是⾼斯分布的似然函数,图像如图1.14所⽰。 使⽤⼀个观测数据集来决定概率分布的参数的⼀个通⽤的标准是寻找使似然函数取得最⼤值 的参数值。这个标准看起来可能很奇怪,因为从我们之前对于概率论的讨论来看,似乎在给定 数据集的情况下最⼤化概率的参数(⽽不是在给定参数的情况下最⼤化数据集出现的概率)是 更加⾃然的。事实上,这两个标准是相关的。我们后⾯将使⽤曲线拟合的例⼦来说明这⼀点。 但是现在,我们要通过最⼤化似然函数(1.53)来确定⾼斯分布中未知的参数µ和σ 2。实际 应⽤中,考虑似然函数的对数值更⽅便。由于对数函数是⼀个单调递增函数,最⼤化某个函数 的对数等价于最⼤化这个函数。取对数不仅简化了后续数学分析,也有助于数值计算,因为⼤ 量⼩概率的乘积很容易下溢,这可以通过计算对数概率的和的⽅式来解决。根据公式(1.46)和 公式(1.53),对数似然函数可以写成 ln p(x | µ, σ2 ) = − 1 2σ 2 ∑ N n=1 (xn − µ) 2 − N 2 ln σ 2 − N 2 ln(2π) (1.54) 关于µ,最⼤化函数(1.54),我们可以得到最⼤似然解 µML = 1 N ∑ N n=1 xn (1.55) 这是样本均值(sample mean),即观测值{xn}的均值。类似地,关于σ 2最⼤化函数(1.54), 我们得到了⽅差的最⼤似然解 σ 2 ML = 1 N ∑ N n=1 (xn − µML) 2 (1.56) 这是关于样本均值µML的样本⽅差(sample variance)。注意,我们要同时关于µ和σ 2来最⼤ 化函数(1.54),但是在⾼斯分布的情况下,µ的解和σ 2⽆关,因此我们可以⾸先估计公式 (1.55)然后使⽤这个结果来估计公式(1.56)。 25