
0 0 0 0 图12:由N=10个数据点组成的训练集的图像,用蓝色圆圈标记。每个数据点由输入变量x的观测以及 对应的目标变量组成。绿色曲线给出了用来生成数据的si(2x)函数。我们的目标是对于某些新的x值, 预测的值,而无需知道绿色曲线。 y(En;w) In 图13:误差函数(12)对应于每个数据点与函数y(x,w)之间位移(绿色垂直线)的平方和(的一半)。 但是现在,我们要用一种相当非正式的、相当简单的方式来进行曲线拟合。特别地,我们将 使用下面形式的多项式函数来拟合数据: M c,0)=0+0x+u22+.+0MxM=∑u与x (1.1) 1=0 其中M是多项式的阶数(order)),x表示x的j次幂。多项式系数wo,·,wM整体记作向量w。 注意,虽然多项式函数y(x,D)是x的一个非线性函数,它是系数的一个线性函数。类似多项式 函数的这种关于未知参数满足线性关系的函数有着重要的性质,被叫做线性模型,将在第3章和 第4章充分讨论。 系数的值可以通过调整多项式函数拟合训练数据的方式确定。这可以通过最小化误差函数 (error function)的方法实现。误差函数衡量了对于任意给定的w值,函数y(x,w)与训练集数据 的差别。一个简单的应用广泛的误差函数是每个数据点xn的预测值y(xn,w)与目标值tn的平方 和。所以我们最小化 E(w)= (1.2) n=1 其中,因子是为了后续运算方便而加入的。我们将在后续章节中讨论选择这个误差函数的原 因。现在,我们只是简单地注意一下它是一个非负的量,并且当且仅当函数(x,w)对所有的训 练数据点均做出正确预测时,误差函数为零。平方和误差函数的几何表示见图1.3。 我们可以通过选择使得E(w)尽量小的w来解决曲线拟合问题。由于误差函数是系数w的二 11
x t 0 1 −1 0 1 图 1.2: 由N = 10个数据点组成的训练集的图像,⽤蓝⾊圆圈标记。每个数据点由输⼊变量x的观测以及 对应的⽬标变量t组成。绿⾊曲线给出了⽤来⽣成数据的sin(2πx)函数。我们的⽬标是对于某些新的x值, 预测t的值,⽽⽆需知道绿⾊曲线。 t x y(xn, w) tn xn 图 1.3: 误差函数(1.2)对应于每个数据点与函数y(x, w)之间位移(绿⾊垂直线)的平⽅和(的⼀半)。 但是现在,我们要⽤⼀种相当⾮正式的、相当简单的⽅式来进⾏曲线拟合。特别地,我们将 使⽤下⾯形式的多项式函数来拟合数据: y(x, w) = w0 + w1x + w2x 2 + . . . + wMx M = ∑ M j=0 wjx j (1.1) 其中M是多项式的阶数(order),x j表⽰x的j次幂。多项式系数w0, . . . , wM整体记作向量w。 注意,虽然多项式函数y(x, w)是x的⼀个⾮线性函数,它是系数w的⼀个线性函数。类似多项式 函数的这种关于未知参数满⾜线性关系的函数有着重要的性质,被叫做线性模型,将在第3章和 第4章充分讨论。 系数的值可以通过调整多项式函数拟合训练数据的⽅式确定。这可以通过最⼩化误差函数 (error function)的⽅法实现。误差函数衡量了对于任意给定的w值,函数y(x, w)与训练集数据 的差别。⼀个简单的应⽤⼴泛的误差函数是每个数据点xn的预测值y(xn, w)与⽬标值tn的平⽅ 和。所以我们最⼩化 E(w) = 1 2 ∑ N n=1 {y(xn, w) − tn} 2 (1.2) 其中,因⼦1 2是为了后续运算⽅便⽽加⼊的。我们将在后续章节中讨论选择这个误差函数的原 因。现在,我们只是简单地注意⼀下它是⼀个⾮负的量,并且当且仅当函数y(x, w)对所有的训 练数据点均做出正确预测时,误差函数为零。平⽅和误差函数的⼏何表⽰见图1.3。 我们可以通过选择使得E(w)尽量⼩的w来解决曲线拟合问题。由于误差函数是系数w的⼆ 11
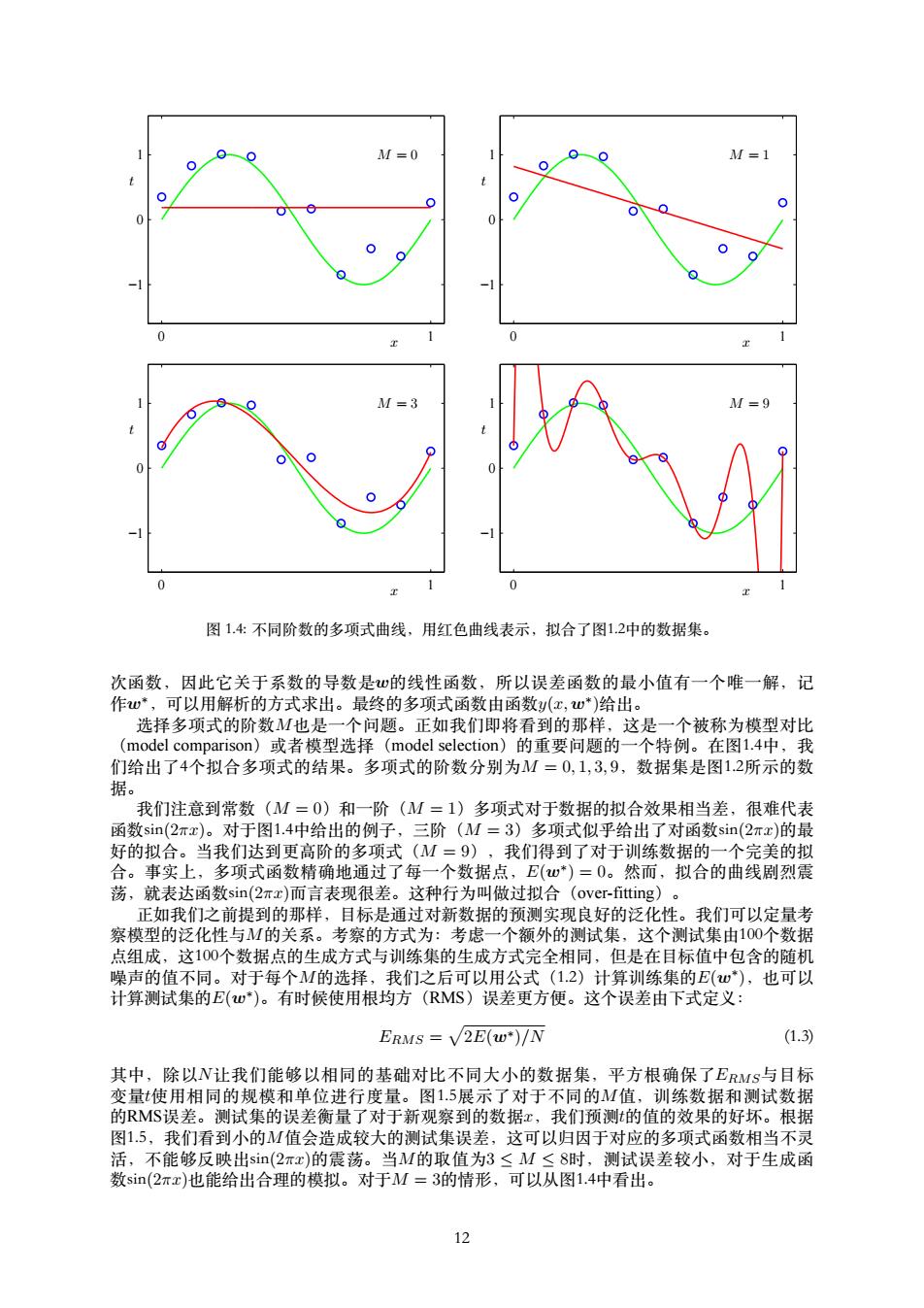
● M=0 M=1 ●) o 0 0 0 M=3 M=9 0 0 0 0 0 图1.4:不同阶数的多项式曲线,用红色曲线表示,拟合了图12中的数据集。 次函数,因此它关于系数的导数是心的线性函数,所以误差函数的最小值有一个唯一解,记 作w*,可以用解析的方式求出。最终的多项式函数由函数y(x,w*)给出。 选择多项式的阶数M也是一个问题。正如我们即将看到的那样,这是一个被称为模型对比 (model comparison)或者模型选择(model selection)的重要问题的一个特例。在图1.4中,我 们给出了4个拟合多项式的结果。多项式的阶数分别为M=0,1,3,9,数据集是图1.2所示的数 据。 我们注意到常数(M=0)和一阶(M=1)多项式对于数据的拟合效果相当差,很难代表 函数sin(2πx)。对于图1.4中给出的例子,三阶(M=3)多项式似乎给出了对函数sin(2πx)的最 好的拟合。当我们达到更高阶的多项式(M=9),我们得到了对于训练数据的一个完美的拟 合。事实上,多项式函数精确地通过了每一个数据点,E(w*)=0。然而,拟合的曲线剧烈震 荡,就表达函数sin(2rx)而言表现很差。这种行为叫做过拟合(over-fitting)。 正如我们之前提到的那样,目标是通过对新数据的预测实现良好的泛化性。我们可以定量考 察模型的泛化性与M的关系。考察的方式为:考虑一个额外的测试集,这个测试集由100个数据 点组成,这100个数据点的生成方式与训练集的生成方式完全相同,但是在目标值中包含的随机 噪声的值不同。对于每个M的选择,我们之后可以用公式(1.2)计算训练集的E(w),也可以 计算测试集的E(w)。有时候使用根均方(RMS)误差更方便。这个误差由下式定义: ERMS =V2E(w*)/N (1.3) 其中,除以N让我们能够以相同的基础对比不同大小的数据集,平方根确保了EMs与目标 变量使用相同的规模和单位进行度量。图1.5展示了对于不同的M值,训练数据和测试数据 的RMS误差。测试集的误差衡量了对于新观察到的数据x,我们预测的值的效果的好坏。根据 图1.5,我们看到小的M值会造成较大的测试集误差,这可以归因于对应的多项式函数相当不灵 活,不能够反映出si(2πx)的震荡。当M的取值为3≤M≤8时,测试误差较小,对于生成函 数sin(2πx)也能给出合理的模拟。对于M=3的情形,可以从图1.4中看出。 12
x t M = 0 0 1 −1 0 1 x t M = 1 0 1 −1 0 1 x t M = 3 0 1 −1 0 1 x t M = 9 0 1 −1 0 1 图 1.4: 不同阶数的多项式曲线,⽤红⾊曲线表⽰,拟合了图1.2中的数据集。 次函数,因此它关于系数的导数是w的线性函数,所以误差函数的最⼩值有⼀个唯⼀解,记 作w∗,可以⽤解析的⽅式求出。最终的多项式函数由函数y(x, w∗ )给出。 选择多项式的阶数M也是⼀个问题。正如我们即将看到的那样,这是⼀个被称为模型对⽐ (model comparison)或者模型选择(model selection)的重要问题的⼀个特例。在图1.4中,我 们给出了4个拟合多项式的结果。多项式的阶数分别为M = 0, 1, 3, 9,数据集是图1.2所⽰的数 据。 我们注意到常数(M = 0)和⼀阶(M = 1)多项式对于数据的拟合效果相当差,很难代表 函数sin(2πx)。对于图1.4中给出的例⼦,三阶(M = 3)多项式似乎给出了对函数sin(2πx)的最 好的拟合。当我们达到更⾼阶的多项式(M = 9),我们得到了对于训练数据的⼀个完美的拟 合。事实上,多项式函数精确地通过了每⼀个数据点,E(w∗ ) = 0。然⽽,拟合的曲线剧烈震 荡,就表达函数sin(2πx)⽽⾔表现很差。这种⾏为叫做过拟合(over-fitting)。 正如我们之前提到的那样,⽬标是通过对新数据的预测实现良好的泛化性。我们可以定量考 察模型的泛化性与M的关系。考察的⽅式为:考虑⼀个额外的测试集,这个测试集由100个数据 点组成,这100个数据点的⽣成⽅式与训练集的⽣成⽅式完全相同,但是在⽬标值中包含的随机 噪声的值不同。对于每个M的选择,我们之后可以⽤公式(1.2)计算训练集的E(w∗ ),也可以 计算测试集的E(w∗ )。有时候使⽤根均⽅(RMS)误差更⽅便。这个误差由下式定义: ERMS = √ 2E(w∗)/N (1.3) 其中,除以N让我们能够以相同的基础对⽐不同⼤⼩的数据集,平⽅根确保了ERMS与⽬标 变量t使⽤相同的规模和单位进⾏度量。图1.5展⽰了对于不同的M值,训练数据和测试数据 的RMS误差。测试集的误差衡量了对于新观察到的数据x,我们预测t的值的效果的好坏。根据 图1.5,我们看到⼩的M值会造成较⼤的测试集误差,这可以归因于对应的多项式函数相当不灵 活,不能够反映出sin(2πx)的震荡。当M的取值为3 ≤ M ≤ 8时,测试误差较⼩,对于⽣成函 数sin(2πx)也能给出合理的模拟。对于M = 3的情形,可以从图1.4中看出。 12

o—Training Test 0.5 6 图1.5:公式(1.3)定义的根均方误差的图像,分别在训练数据集上和独立的测试数据集上对于不同 的M进行了计算。 M=0M=1M=3 M=9 WG 0.19 0.82 0.31 0.35 wi -1.27 7.99 232.37 -25.43 -5321.83 w 17.37 48568.31 -231639.30 u哼 640042.26 w哈 -1061800.52 u呀 1042400.18 -557682.99 w话 125201.43 表11:不同阶数的多项式的系数w*的值。观察随着多项式阶数的增加,系数的大小是如何剧烈增大的。 对于M=9的情形,训练集的误差为0,这符合我们的预期,因为此时的多项式函数有10个 自由度,对应于10个系数o,..,wg,所以可以调节模型的参数,使得模型与训练集中的10个数 据点精确匹配。然而,正如我们在图14中看到的那样,测试集误差变得非常大,对应的函 数y(,w*)表现出剧烈的震荡。 这可能看起来很矛盾,因为给定阶数的多项式包含了所有低阶的多项式函数作为特殊情 况。M=9的多项式因此能够产生至少与M=3一样好的结果。并且,我们可以猜想,对于新 数据最好的预测是s血(2πx),这是生成数据所使用的函数(我们稍后将会看到确实是这样)。我 们知道函数si(2πx)的幂级数展开包含所有阶数的项,所以我们可能会以为结果会随着M的增 大而单调地变好。 我们可以更深刻地思考这个问题,通过考察不同阶数多项式的系数w*的值,如表1.1所示。 我们看到随着M的增大,系数的大小通常会变大。对于M=9的多项式,通过调节系数,让系 数取相当大的正数或者负数,多项式函数可以精确地与数据匹配,但是对于数据之间的点(尤 其是临近区间端点处的点),从图1.4可以看到函数表现出剧烈的震荡。直觉上讲,发生了这样 的事情:有着更大的M值的更灵活的多项式被过分地调参,使得多项式被调节成了与目标值的 随机噪声相符。 考察给定模型的行为随着数据集规模的变化情况也很有趣,如图1.6所示。我们可以看到, 对已一个给定的模型复杂度,当数据集的规模增加时,过拟合问题变得不那么严重。另一种表 述方式是,数据集规模越大,我们能够用来拟合数据的模型就越复杂(即越灵活)。一个粗略 的启发是,数据点的数量不应该小于模型的可调节参数的数量的若干倍(比如5或10)。然而, 正如我们将在第3章看到的那样,参数的数量对于模型复杂度的大部分合理的度量来说都不是必 要的。 13
M ERMS 0 3 6 9 0 0.5 1 Training Test 图 1.5: 公式(1.3)定义的根均⽅误差的图像,分别在训练数据集上和独⽴的测试数据集上对于不同 的M进⾏了计算。 M = 0 M = 1 M = 3 M = 9 w ∗ 0 0.19 0.82 0.31 0.35 w ∗ 1 -1.27 7.99 232.37 w ∗ 2 -25.43 -5321.83 w ∗ 3 17.37 48568.31 w ∗ 4 -231639.30 w ∗ 5 640042.26 w ∗ 6 -1061800.52 w ∗ 7 1042400.18 w ∗ 8 -557682.99 w ∗ 9 125201.43 表 1.1: 不同阶数的多项式的系数w∗的值。观察随着多项式阶数的增加,系数的⼤⼩是如何剧烈增⼤的。 对于M = 9的情形,训练集的误差为0,这符合我们的预期,因为此时的多项式函数有10个 ⾃由度,对应于10个系数w0, . . . , w9,所以可以调节模型的参数,使得模型与训练集中的10个数 据点精确匹配。然⽽,正如我们在图1.4中看到的那样,测试集误差变得⾮常⼤,对应的函 数y(x, w∗ )表现出剧烈的震荡。 这可能看起来很⽭盾,因为给定阶数的多项式包含了所有低阶的多项式函数作为特殊情 况。M = 9的多项式因此能够产⽣⾄少与M = 3⼀样好的结果。并且,我们可以猜想,对于新 数据最好的预测是sin(2πx),这是⽣成数据所使⽤的函数(我们稍后将会看到确实是这样)。我 们知道函数sin(2πx)的幂级数展开包含所有阶数的项,所以我们可能会以为结果会随着M的增 ⼤⽽单调地变好。 我们可以更深刻地思考这个问题,通过考察不同阶数多项式的系数w∗的值,如表1.1所⽰。 我们看到随着M的增⼤,系数的⼤⼩通常会变⼤。对于M = 9的多项式,通过调节系数,让系 数取相当⼤的正数或者负数,多项式函数可以精确地与数据匹配,但是对于数据之间的点(尤 其是临近区间端点处的点),从图1.4可以看到函数表现出剧烈的震荡。直觉上讲,发⽣了这样 的事情:有着更⼤的M值的更灵活的多项式被过分地调参,使得多项式被调节成了与⽬标值的 随机噪声相符。 考察给定模型的⾏为随着数据集规模的变化情况也很有趣,如图1.6所⽰。我们可以看到, 对已⼀个给定的模型复杂度,当数据集的规模增加时,过拟合问题变得不那么严重。另⼀种表 述⽅式是,数据集规模越⼤,我们能够⽤来拟合数据的模型就越复杂(即越灵活)。⼀个粗略 的启发是,数据点的数量不应该⼩于模型的可调节参数的数量的若⼲倍(⽐如5或10)。然⽽, 正如我们将在第3章看到的那样,参数的数量对于模型复杂度的⼤部分合理的度量来说都不是必 要的。 13

0 N=15 o08 88 0 N=100 。 0 0 0 0 o0go 000 ·8o98 80o0 ● 0 dD 0 1 图1.6:使用M=9的多项式对M=15个数据点(左图)和N=100个数据点(右图)通过最小化平方和 误差函数的方法得到的解。我们看到增大数据集的规模会减小过拟合问题。 并且,令人无法满意的一点是,不得不根据可得到的训练集的规模限制参数的数量。似乎更 加合理的是,根据待解决的问题的复杂性来选择模型的复杂性。我们将会看到,寻找模型参数 的最小平方方法代表了最大似然(maximum likelihood)(将在1.2.5节讨论)的一种特殊情形, 并且过拟合问题可以被理解为最大似然的一个通用属性。通过使用一种贝叶斯(Bayesian)方 法,过拟合问题可以被避免。我们将会看到,从贝叶斯的观点来看,对于模型参数的数量超过 数据点数量的情形,没有任何难解之处。实际上,一个贝叶斯模型中,参数的有效(effective) 数量会自动根据数据集的规模调节。 但是现在,继续使用当前的方法还是很有用的。并且考虑在实际中我们可以如何应用有限规 模的数据集也是很有意义的。在这种情况下,我们可能期望建立相对复杂和灵活的模型。经 常用来控制过拟合现象的一种技术是正则化(regularization)。这种技术涉及到给误差函数 (1.2)增加一个惩罚项,使得系数不会达到很大的值。这种惩罚项最简单的形式采用所有系数 的平方和的形式。这推导出了误差函数的修改后的形式: (w) fu(za.w)-ta)2+ (1.4) n=1 其中w2≡wTw=w哈+w?+·+w,系数入控制了正则化项相对于平方和误差项的重要 性。注意,通常系数0从正则化项中省略,因为包含0会使得结果依赖于目标变量原点的选择 (Hastie et al.,2001)。wo也可以被包含在正则化项中,但是必须有自己的正则化系数(我们将 在5.5.1节详细讨论这个问题)。公式(1.4)中的误差函数也可以用解析的形式求出最小值。像 这样的技术在统计学的文献中被叫做收缩(shrinkage)方法,因为这种方法减小了系数的值。 二次正则项的一个特殊情况被称为山脊回归(ridge regression)(Hoerl and Kennard,I970)。在 神经网络的情形中,这种方法被叫做权值衰减(weight decay)。 图1.7展示了在M=9的情况下用与之前相同的数据拟合多项式的结果。这次使用的是公式 (1.4)的正则化误差函数。我们看到,对于1入=-18,过拟合现象被压制,我们可以得到关 于本质函数sn(2πx)的一个更好的模拟。但是如果我们把入选择的过大,我们又得到了一个不好 的结果,如图1.7所示的1n入=0的情形。拟合的多项式的对应的系数在表1.2中给出,表明正则 化在减小系数的值方面产生了预期的效果。 正则化项对于泛化错误的影响可以从图1.8看出。图1.8给出了训练集和测试集的RMS误差 与l入的关系。我们看到,在效果上,入控制了模型的复杂性,因此决定了过拟合的程度。 模型复杂度是一个重要的话题,将在13节详细讨论。这里我们简单地说一下,如果我们试 着用最小化误差函数的方法解决一个实际的应用问题,那么我们不得不寻找一种方式来确定模 型复杂度的合适值。上面的结果给出了一种完成这一目标的简单方式,即通过把给定的数据中 的一部分从测试集中分离出,来确定系数w。这个分离出来的验证集(validation set),也被称 为拿出集(hold-out set)),用来最优化模型的复杂度(M或者入)。但是在许多情况下,这太浪 费有价值的训练数据了,我们不得不寻找更高级的方法。 14
x t N = 15 0 1 −1 0 1 x t N = 100 0 1 −1 0 1 图 1.6: 使⽤M = 9的多项式对M = 15个数据点(左图)和N = 100个数据点(右图)通过最⼩化平⽅和 误差函数的⽅法得到的解。我们看到增⼤数据集的规模会减⼩过拟合问题。 并且,令⼈⽆法满意的⼀点是,不得不根据可得到的训练集的规模限制参数的数量。似乎更 加合理的是,根据待解决的问题的复杂性来选择模型的复杂性。我们将会看到,寻找模型参数 的最⼩平⽅⽅法代表了最⼤似然(maximum likelihood)(将在1.2.5节讨论)的⼀种特殊情形, 并且过拟合问题可以被理解为最⼤似然的⼀个通⽤属性。通过使⽤⼀种贝叶斯(Bayesian)⽅ 法,过拟合问题可以被避免。我们将会看到,从贝叶斯的观点来看,对于模型参数的数量超过 数据点数量的情形,没有任何难解之处。实际上,⼀个贝叶斯模型中,参数的有效(effective) 数量会⾃动根据数据集的规模调节。 但是现在,继续使⽤当前的⽅法还是很有⽤的。并且考虑在实际中我们可以如何应⽤有限规 模的数据集也是很有意义的。在这种情况下,我们可能期望建⽴相对复杂和灵活的模型。经 常⽤来控制过拟合现象的⼀种技术是正则化(regularization)。这种技术涉及到给误差函数 (1.2)增加⼀个惩罚项,使得系数不会达到很⼤的值。这种惩罚项最简单的形式采⽤所有系数 的平⽅和的形式。这推导出了误差函数的修改后的形式: E˜(w) = 1 2 ∑ N n=1 {y(xn, w) − tn} 2 + λ 2 ∥w∥ 2 (1.4) 其中∥w∥ 2 ≡ wT w = w 2 0 + w 2 1 + . . . + w 2 M,系数λ控制了正则化项相对于平⽅和误差项的重要 性。注意,通常系数w0从正则化项中省略,因为包含w0会使得结果依赖于⽬标变量原点的选择 (Hastie et al., 2001)。w0也可以被包含在正则化项中,但是必须有⾃⼰的正则化系数(我们将 在5.5.1节详细讨论这个问题)。公式(1.4)中的误差函数也可以⽤解析的形式求出最⼩值。像 这样的技术在统计学的⽂献中被叫做收缩(shrinkage)⽅法,因为这种⽅法减⼩了系数的值。 ⼆次正则项的⼀个特殊情况被称为⼭脊回归(ridge regression)(Hoerl and Kennard, 1970)。在 神经⽹络的情形中,这种⽅法被叫做权值衰减(weight decay)。 图1.7展⽰了在M = 9的情况下⽤与之前相同的数据拟合多项式的结果。这次使⽤的是公式 (1.4)的正则化误差函数。我们看到,对于ln λ = −18,过拟合现象被压制,我们可以得到关 于本质函数sin(2πx)的⼀个更好的模拟。但是如果我们把λ选择的过⼤,我们又得到了⼀个不好 的结果,如图1.7所⽰的ln λ = 0的情形。拟合的多项式的对应的系数在表1.2中给出,表明正则 化在减⼩系数的值⽅⾯产⽣了预期的效果。 正则化项对于泛化错误的影响可以从图1.8看出。图1.8给出了训练集和测试集的RMS误差 与ln λ的关系。我们看到,在效果上,λ控制了模型的复杂性,因此决定了过拟合的程度。 模型复杂度是⼀个重要的话题,将在1.3节详细讨论。这⾥我们简单地说⼀下,如果我们试 着⽤最⼩化误差函数的⽅法解决⼀个实际的应⽤问题,那么我们不得不寻找⼀种⽅式来确定模 型复杂度的合适值。上⾯的结果给出了⼀种完成这⼀⽬标的简单⽅式,即通过把给定的数据中 的⼀部分从测试集中分离出,来确定系数w。这个分离出来的验证集(validation set),也被称 为拿出集(hold-out set),⽤来最优化模型的复杂度(M或者λ)。但是在许多情况下,这太浪 费有价值的训练数据了,我们不得不寻找更⾼级的⽅法。 14
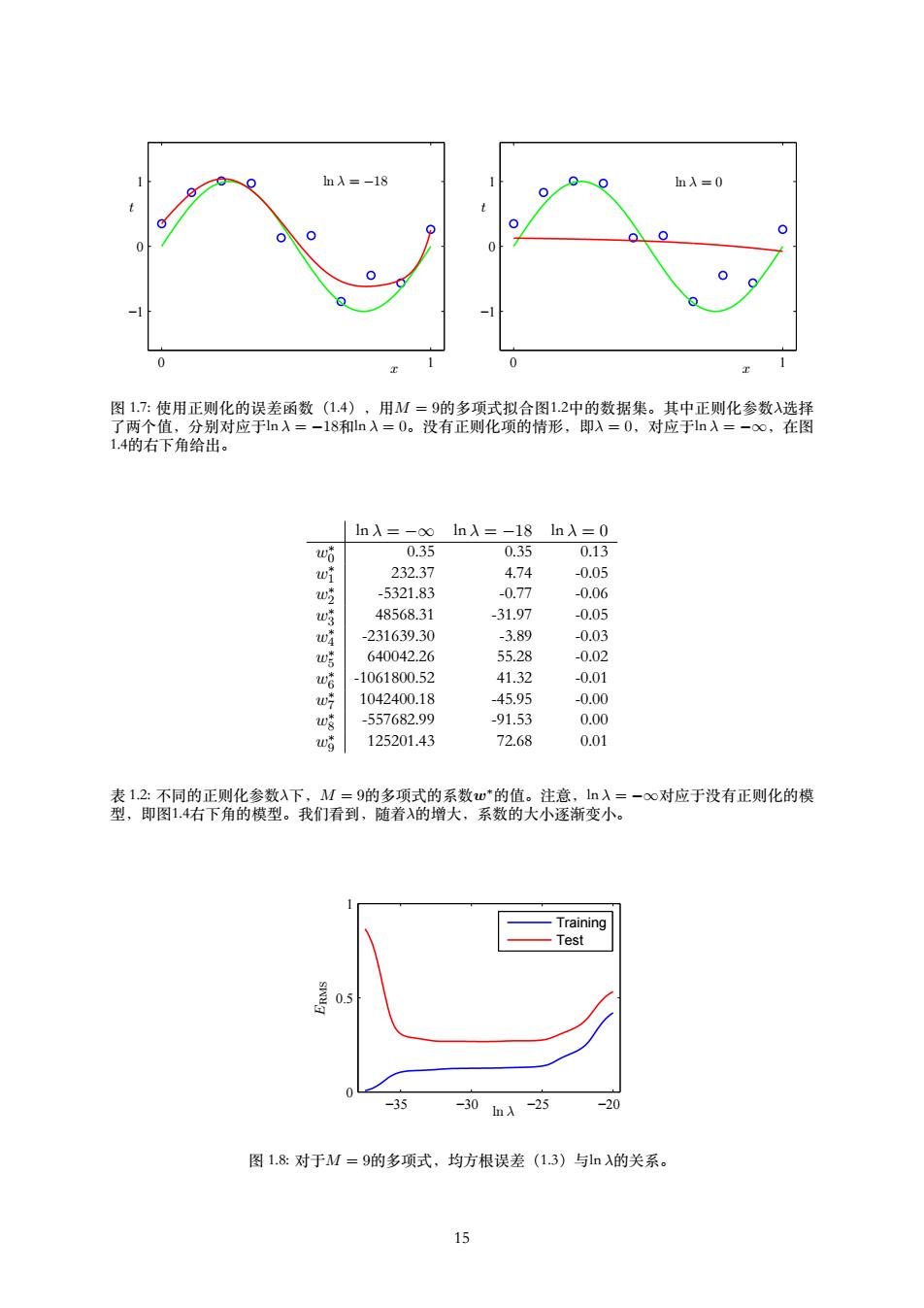
1mλ=-18 0 nλ=0 0 0 0 -1 0 0 1 图1.7:使用正则化的误差函数(1.4),用M=9的多项式拟合图1.2中的数据集。其中正则化参数入选择 了两个值,分别对应于ln入=-l8和ln入=0。没有正则化项的情形,即入=0,对应于ln入=-oo,在图 1.4的右下角给出。 ln入=-∞ ln入=-18ln入=0 w哈 0.35 0.35 0.13 wf 232.37 4.74 -0.05 w吃 -5321.83 -0.77 -0.06 w 48568.31 -31.97 -0.05 w -231639.30 -3.89 -0.03 w哼 640042.26 55.28 -0.02 -1061800.52 41.32 -0.01 w 1042400.18 -45.95 -0.00 -557682.99 -91.53 0.00 125201.43 72.68 0.01 表1.2:不同的正则化参数入下,M=9的多项式的系数w*的值。注意,1n入=-oo对应于没有正则化的模 型,即图1.4右下角的模型。我们看到,随着入的增大,系数的大小逐渐变小。 Training Test 0.5 -35 -30hA-25 -20 图1.8:对于M=9的多项式,均方根误差(1.3)与n的关系。 15
x t ln λ = −18 0 1 −1 0 1 x t ln λ = 0 0 1 −1 0 1 图 1.7: 使⽤正则化的误差函数(1.4),⽤M = 9的多项式拟合图1.2中的数据集。其中正则化参数λ选择 了两个值,分别对应于ln λ = −18和ln λ = 0。没有正则化项的情形,即λ = 0,对应于ln λ = −∞,在图 1.4的右下⾓给出。 ln λ = −∞ ln λ = −18 ln λ = 0 w ∗ 0 0.35 0.35 0.13 w ∗ 1 232.37 4.74 -0.05 w ∗ 2 -5321.83 -0.77 -0.06 w ∗ 3 48568.31 -31.97 -0.05 w ∗ 4 -231639.30 -3.89 -0.03 w ∗ 5 640042.26 55.28 -0.02 w ∗ 6 -1061800.52 41.32 -0.01 w ∗ 7 1042400.18 -45.95 -0.00 w ∗ 8 -557682.99 -91.53 0.00 w ∗ 9 125201.43 72.68 0.01 表 1.2: 不同的正则化参数λ下,M = 9的多项式的系数w∗的值。注意,ln λ = −∞对应于没有正则化的模 型,即图1.4右下⾓的模型。我们看到,随着λ的增⼤,系数的⼤⼩逐渐变⼩。 ERMS ln λ −35 −30 −25 −20 0 0.5 1 Training Test 图 1.8: 对于M = 9的多项式,均⽅根误差(1.3)与ln λ的关系。 15