
22动量定理动量守恒定律 2.2动量定理动量守恒定律 一.质点的动量定理 由牛顿第二定律的微分形式 Fdt=d项 积分」 Fa=[dp=p-D 1.力的冲量1-么F t(过程量) 前页后页且录 1
前页 后页 目录 1 2.2 动量定理 动量守恒定律 由牛顿第二定律的微分形式 积分 2 2 1 1 d d t p t p F t p = 1.力的冲量 2 1 d t t I F t = 2.2 动量定理 动量守恒定律 一. 质点的动量定理 2 1 = − p p (过程量) F t p d d =

22动量定理动量守恒定律 2.动量定理 物体在运动过程中所受到的合外力的冲量,等 于该物体动量的增量。 I=p2-P 讨论: 1)牛顿第二定律的积分形式之一 2)适用于惯性系 3)质,点系只须考虑外力 4)处理变质量问题 5)矢量性 前页后页目录 2
前页 后页 目录 2 2.2 动量定理 动量守恒定律 2 1 I p p = − 2.动量定理 物体在运动过程中所受到的合外力的冲量,等 于该物体动量的增量。 讨论: 1)牛顿第二定律的积分形式之一 2)适用于惯性系 3)质点系只须考虑外力 4)处理变质量问题 5)矢量性
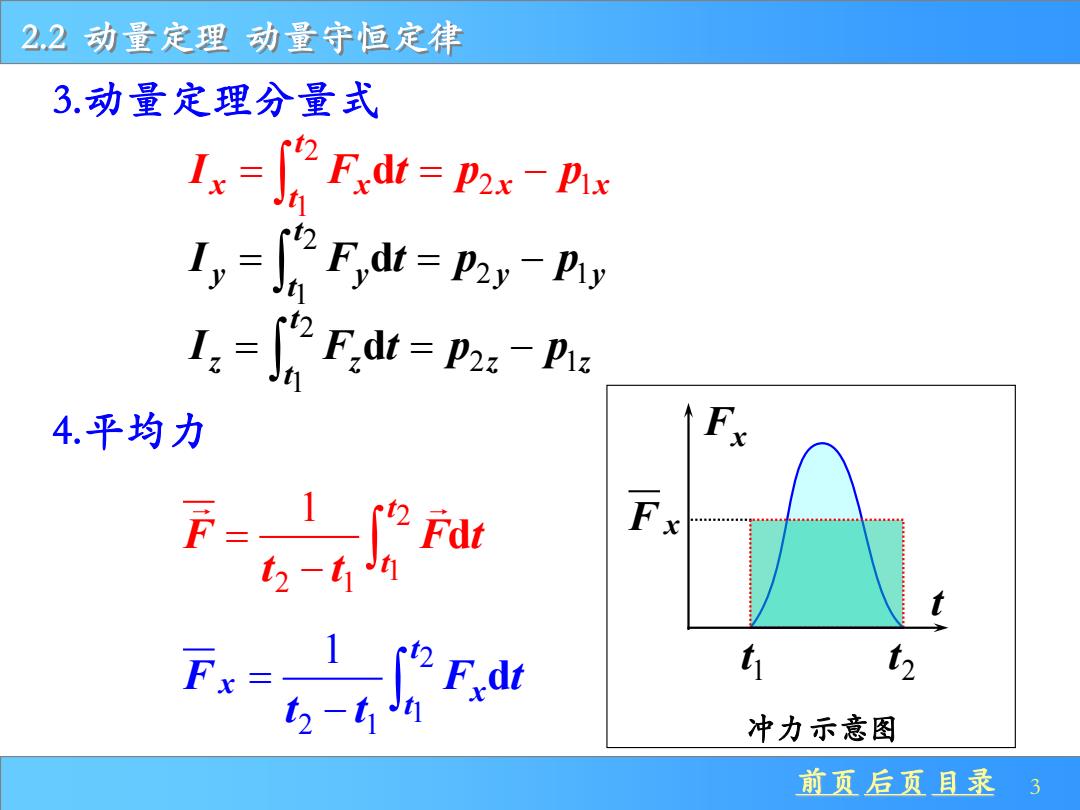
2.2动量定理动量守恒定律 3.动量定理分量式 1-F-P- =0 F,dt=p2y-Phiy Fdt=P2:-Phe 4.平均力 F Fx 年088年8828年0年88 万:m t 冲力示意图 前页后页目录3
前页 后页 目录 3 2.2 动量定理 动量守恒定律 3.动量定理分量式 2 2 1 1 d t x x x x t I F t p p = = − 2 2 1 1 d t y y y y t I F t p p = = − 2 2 1 1 d t z z z z t I F t p p = = − 4.平均力 2 1 2 1 1 d t t F F t t t = − 2 1 2 1 1 d t x x t F F t t t = − t 1 t 2 t Fx F x 冲力示意图

2.2动量定理动量守恒定律 5.质,点系动量定理 两个物体分别应用动量定理 +2= dp dr 2 万+61 d m dt 两式相加,并应用牛顿第三定律f2+f1=0 R+B=+) 前页后页且录4
前页 后页 目录 4 2.2 动量定理 动量守恒定律 5.质点系动量定理 两个物体分别应用动量定理 两式相加,并应用牛顿第三定律 12 f F1 m1 21 f m2 F2 12 21 f f + = 0 1 1 12 d d p F f t + = 2 2 21 d d p F f t + = 1 2 1 2 d ( ) d F F p p t + = +

22动量定理动量守恒定律 推广到任意个物体 东Σn 简写成F= dt 微分形式 令F=∑ Fdt dp p=∑p 积分形式 欢=p-m 讨论: 1)只计外力的失量和,可不计内力 2)与质点动量定理形式相同 前页后页目录5
前页 后页 目录 5 2.2 动量定理 动量守恒定律 推广到任意个物体 简写成 微分形式 积分形式 讨论: 1)只计外力的矢量和,可不计内力 2)与质点动量定理形式相同 d d i i i i F p t = d d p F t = F t p d d = 2 2 1 1 d t t F t p p = − i i F F = i i p p = 令