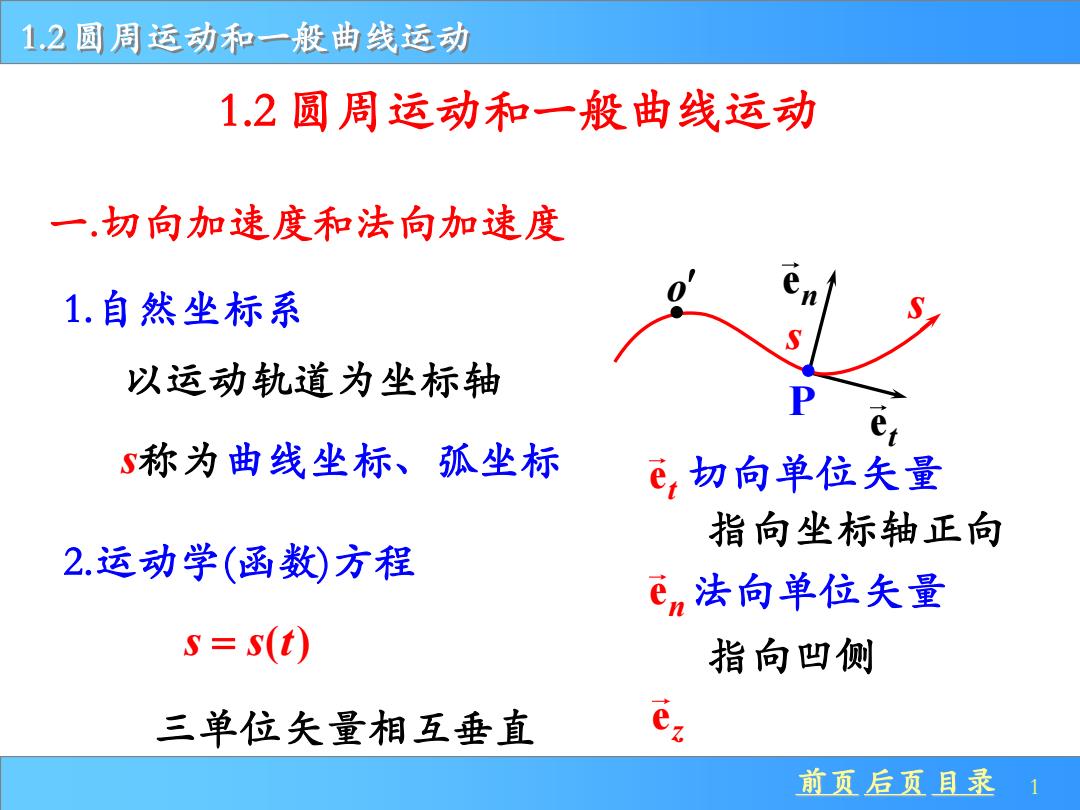
1.2圆周运动和一般曲线运动 1.2圆周运动和一般曲线运动 一.切向加速度和法向加速度 1.自然坐标系 以运动轨道为坐标轴 S称为曲线坐标、孤坐标 e,切向单位夫量 指向坐标轴正向 2.运动学(函数)方程 en法向单位矢量 s=s(t) 指向凹侧 三单位失量相互垂直 前页后页且录 1
前页 后页 目录 1 1.2 圆周运动和一般曲线运动 一.切向加速度和法向加速度 1.自然坐标系 en et P o s称为曲线坐标、弧坐标 et 切向单位矢量 en 法向单位矢量 2.运动学(函数)方程 s s t = ( ) 1.2 圆周运动和一般曲线运动 以运动轨道为坐标轴 s s 指向坐标轴正向 指向凹侧 e 三单位矢量相互垂直 z
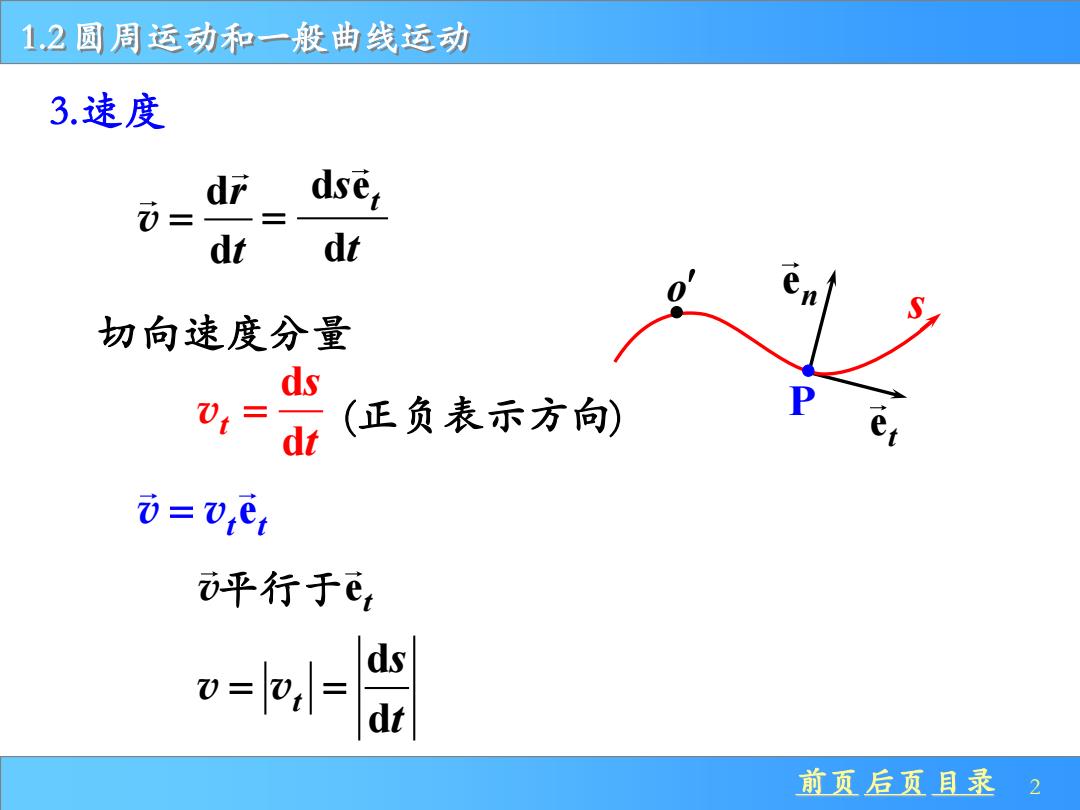
1.2圆周运动和一般曲线运动 3.速度 U= dr dse, dt dt S 切向速度分量 ds ,= (正负表示方向) P D=ve, ⑦平行于e o== ds 前页后页目录2
前页 后页 目录 2 1.2 圆周运动和一般曲线运动 3.速度 dt = d d t s t v = e v v = t t d d t s t v v = = 切向速度分量 en et P o s d et s e v平行于 t d d r t v = (正负表示方向)
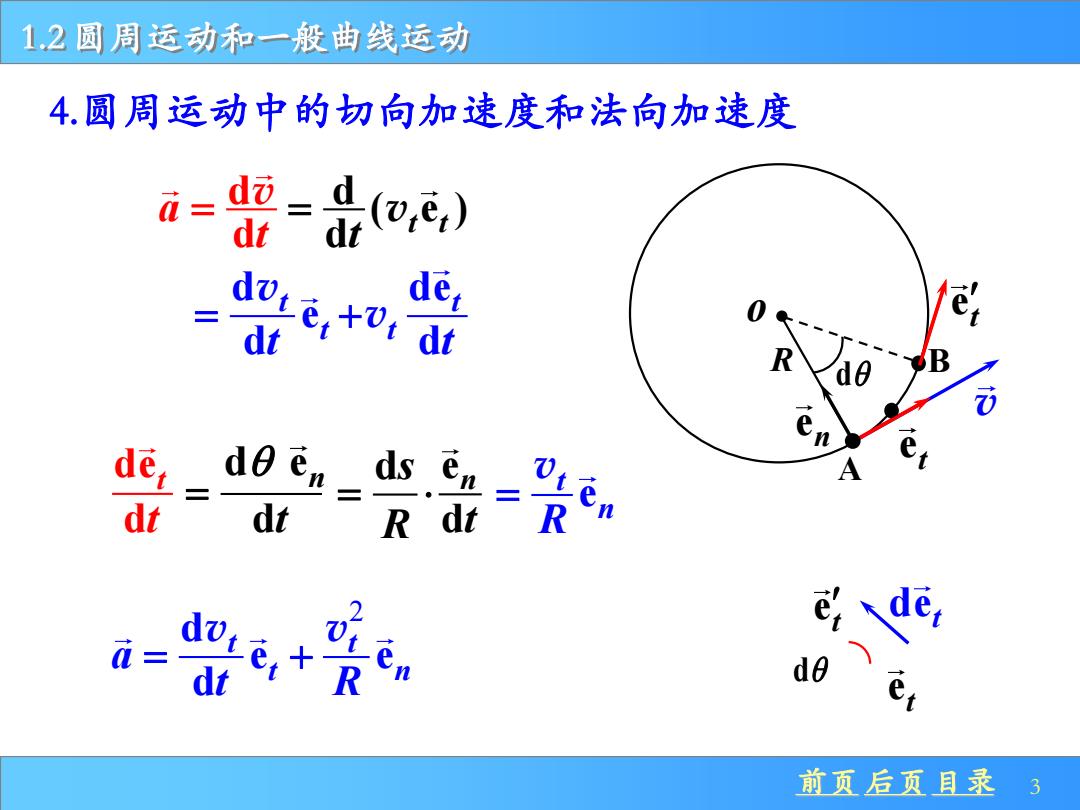
1.2圆周运动和一般曲线运动 4.圆周运动中的切向加速度和法向加速度 a-d dt 出oe,) = de; 二 dt t dt R de, ds 0 A dt dt R dt R dt 前页后页目录3
前页 后页 目录 3 1.2 圆周运动和一般曲线运动 v et et d det o e A t R B en d et 4.圆周运动中的切向加速度和法向加速度 d d a t = v d ( e ) d t t t = v de d t t dt = ds R = e t n R = v 2 d e e d t t t n a t R = + v v d e d t t t = v de d t t t +v d en e d n t
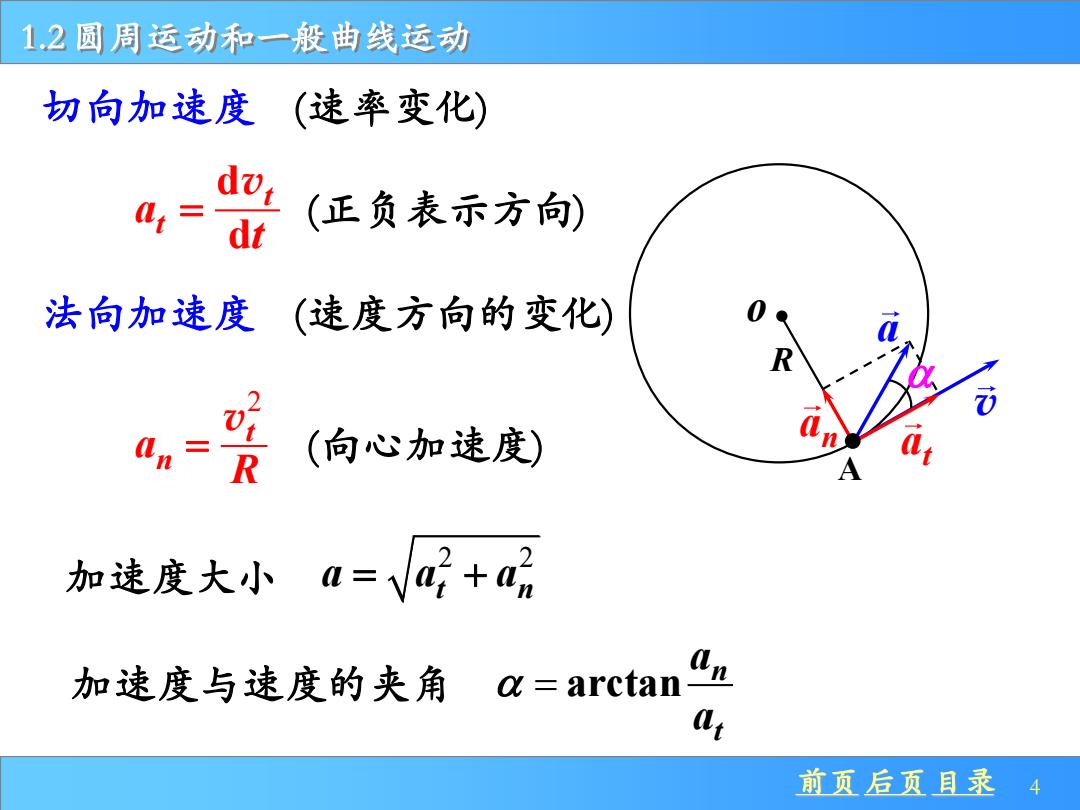
12圆周运动和一般曲线运动 切向加速度(速率变化) = dt (正负表示方向) 法向加速度 (速度方向的变化) R 0n= R (向心加速度) A 加速度大小a=V@+肠 加速度与速度的夹角a=arctan 前页后页且录4
前页 后页 目录 4 1.2 圆周运动和一般曲线运动 v n a t a a 切向加速度 d d t t a t = v (速率变化) 法向加速度 2 t n a R = v 2 2 t n a a a = + arctan n t a a = (速度方向的变化) 加速度大小 加速度与速度的夹角 o A R (向心加速度) (正负表示方向)
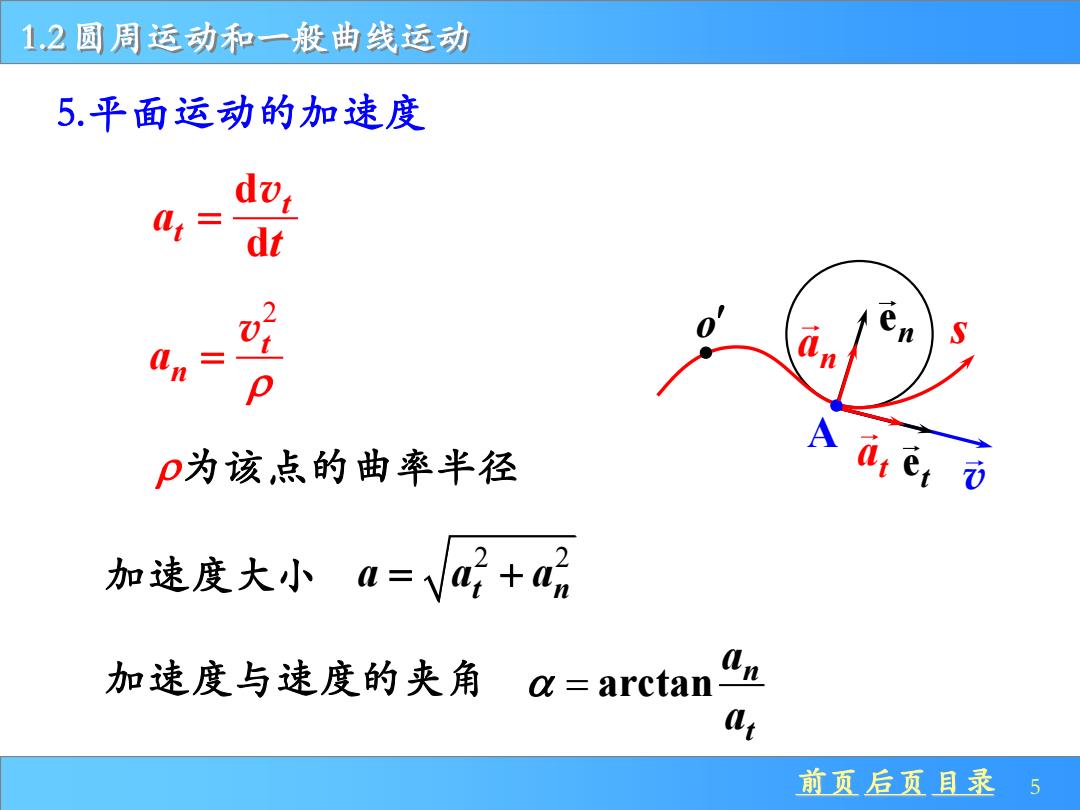
12圆周运动和一般曲线运动 5.平面运动的加速度 = in en S n P为该,点的曲率半径 Aae i 加速度大小a=Va好+ 加速度与速度的夹角a=arctan a; 前页后页目录5
前页 后页 目录 5 1.2 圆周运动和一般曲线运动 en et o s v t a n a A 5.平面运动的加速度 d d t t a t = v 2 t n a = v 为该点的曲率半径 加速度大小 加速度与速度的夹角 2 2 t n a a a = + arctan n t a a =