
氏零度时的电流值,该值恰好与冰点的热力学温度273K相对应(实际使用时,应放 在冰点温度时进行确定)。利用AD590集成电路温度传感器的上述特性,可以制成各 种用途的温度计。在通常实验时,采取测量取样电阻R上的电压求得电流I。 【实验装置】 型通体批汽化热到量位。对e每城::: 图1实验装置图 A烧瓶盖;B烧瓶:C通汽玻璃管:D托盘:E电炉;F绝热板:G橡皮管: H量热器外壳;I绝热材料;J量热器内杯:K铝说拌器;L、AD590:M温控和测量仪表 【实验步骤】 1、集成电路温度传感器D590的定标。 10
10 氏零度时的电流值,该值恰好与冰点的热力学温度 273K 相对应(实际使用时,应放 在冰点温度时进行确定)。利用 AD590 集成电路温度传感器的上述特性,可以制成各 种用途的温度计。在通常实验时,采取测量取样电阻 R 上的电压求得电流 I。 【实验装置】 【实验步骤】 1、集成电路温度传感器 AD590 的定标

每个集成电路温度传感的灵敏度有所不同,在实验前,应将其定标。按图2要求接 线。(实际在我们提供的测量仪器中已经接好电阻为10002±1%,数字电压表为四位 半,传感器加电源电压为6V。你只要把AD590的红黑接线分别插入面板上的输入孔 即可进行定标或测量)。把实验数据用最小二乘法进行直线拟合,求得斜率B,截距 A和相关系数r。 AD590 (mV 图2 2、水汽化热的实验: ①、用物理天平或电子天平秤量热器和搅拌器的质量m+,然后在量热器内杯中加 一定量的水,再秤出盛有水的量热器和搅拌器的质量减去m+皿得到水的质量m。 ②、将盛有水的量热器的内杯放在冰块上,预冷却到室温以下较低的温度。但被冷却 水的温度须高于环境的露点,如果低于露点,则实验过程中量热器内杯的外表有可 能凝结上簿水层,从而释放出热量,影响测量结果。将预冷过的内杯放到量热器内 再放在水蒸汽管下,使通气汽橡皮管插入水中约1米深,注意气管不宜插入太深,以 防止通气管堵塞。 ③、将盛有水的烧瓶加热,开始加热时可以通过温控电位器顺时针调到底,此时瓶 盖移去,使低于100℃的水蒸汽从瓶口逸出。当烧瓶内水沸腾时可以由温控器调节, 保证水蒸汽输入量热器的速率附合实验要求。这时要首先读下温度仪的数值01。接 着把瓶盖盖好继续让水沸腾向量热器的水中通蒸汽并搅拌量热器内的水,通过时间 长短,以尽可能使量热器中水的未温度:与室温的温差同室温与初温0,差值相 近,这样可使实验过程中量热器内杯与外界热交换相抵消。 ④、停止电炉通电,并打开瓶盖不再向量热器通汽,继续搅拌量热器内杯的水,读 出水和内杯的未温度O2。再一次秤量出量热器内杯水的总质量M。经过计算,求得 量热器中水蒸汽的质量M=M一场。(为未通气前,量热器内杯、搅拌器和水的总 质量) ⑤、将所得到的测量结果代入公式(1),即求得水在100C时的比汽化热。 【实验数据和结果】 集成电路温度传感器AD590定标结果。 11
11 每个集成电路温度传感的灵敏度有所不同,在实验前,应将其定标。按图 2 要求接 线。(实际在我们提供的测量仪器中已经接好电阻为 1000 1%,数字电压表为四位 半,传感器加电源电压为 6V。你只要把 AD590 的红黑接线分别插入面板上的输入孔 即可进行定标或测量)。把实验数据用最小二乘法进行直线拟合,求得斜率 B,截距 A 和相关系数r。 图 2 2、水汽化热的实验: ①、用物理天平或电子天平秤量热器和搅拌器的质量 m1+m2,然后在量热器内杯中加 一定量的水,再秤出盛有水的量热器和搅拌器的质量减去 m1+m2得到水的质量 m。 ②、将盛有水的量热器的内杯放在冰块上,预冷却到室温以下较低的温度。但被冷却 水的温度须高于环境的露点,如果低于露点,则实验过程中量热器内杯的外表有可 能凝结上簿水层,从而释放出热量,影响测量结果。将预冷过的内杯放到量热器内 再放在水蒸汽管下,使通气汽橡皮管插入水中约 1 米深,注意气管不宜插入太深,以 防止通气管堵塞。 ③、将盛有水的烧瓶加热,开始加热时可以通过温控电位器顺时针调到底,此时瓶 盖移去,使低于 100 C 0 的水蒸汽从瓶口逸出。当烧瓶内水沸腾时可以由温控器调节, 保证水蒸汽输入量热器的速率附合实验要求。这时要首先读下温度仪的数值 1。接 着把瓶盖盖好继续让水沸腾向量热器的水中通蒸汽并搅拌量热器内的水,通过时间 长短,以尽可能使量热器中水的未温度 2 与室温的温差同室温与初温 1 差值相 近,这样可使实验过程中量热器内杯与外界热交换相抵消。 ④、停止电炉通电,并打开瓶盖不再向量热器通汽,继续搅拌量热器内杯的水,读 出水和内杯的未温度 2。再一次秤量出量热器内杯水的总质量 M 总。经过计算,求得 量热器中水蒸汽的质量 M=M 总-M0。(M0为未通气前,量热器内杯、搅拌器和水的总 质量) ⑤、将所得到的测量结果代入公式(1),即求得水在 100 C 0 时的比汽化热。 【实验数据和结果】 集成电路温度传感器 AD590 定标结果
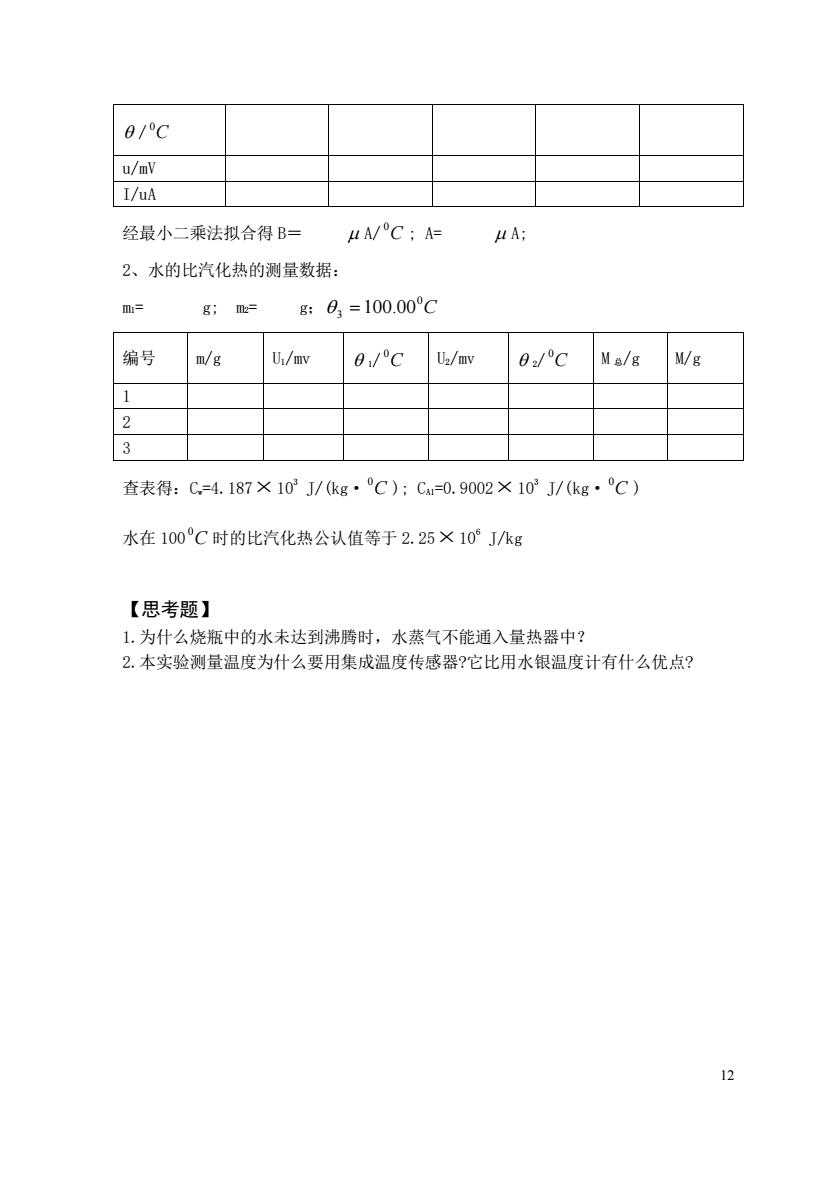
0/c wmy I/uA 经最小二乘法拟合得B= uA/C:A= MA: 2、水的比汽化热的测量数据: m= g;m= g:93=100.00°C 编号 n/g U:/mv 0/°Cz/mv 0/C Ma/g W/g 1 2 3 查表得:C=4.187×103J/kg·C):Ca=0.9002×103J/(kg·C) 水在100°C时的比汽化热公认值等于2.25×10°J/kg 【思考题】 1.为什么烧瓶中的水未达到沸腾时,水蒸气不能通入量热器中? 2.本实验测量温度为什么要用集成温度传感器?它比用水银温度计有什么优点? 12
12 / C 0 u/mV I/uA 经最小二乘法拟合得 B= A/ C 0 ; A= A; 2、水的比汽化热的测量数据: m1= g; m2= g; C 0 3 = 100.00 编号 m/g U1/mv 1/ C 0 U2/mv 2/ C 0 M 总/g M/g 1 2 3 查表得:Cw=4.187 103 J/(kg· C 0 ); CA1=0.9002 103 J/(kg· C 0 ) 水在 100 C 0 时的比汽化热公认值等于 2.25 106 J/kg 【思考题】 1.为什么烧瓶中的水未达到沸腾时,水蒸气不能通入量热器中? 2.本实验测量温度为什么要用集成温度传感器?它比用水银温度计有什么优点?

实验三受迫振动 在机械制造和建筑工程等科技领域中受迫振动所导致的共振现象引起工程技术 人员极大注意,既有破坏作用,但也有许多实用价值。众多电声器件是运用共振原 理设计制作的。此外,在微观科学研究中“共振”也是一种重要研究手段,例如利 用核磁共振和顺磁共振研究物质结构等。 表征受迫振动性质是受迫振动的振幅一频率特性和相位一频率特性(简称幅频 和相频特性)。 本实验中采用玻尔共振仪定量测定机械受迫振动的幅频特性和相频特性,并利 用频闪方法来测定动态的物理量一相位差。 【实验目的】 1.研究玻尔共振仪中弹性摆轮受迫振动的幅频特性和相频特性。 2.研究不同阻尼力矩对受迫振动的影响,观察共振现象。 3.学习用频闪法测定运动物体的某些量,例相位差。 4 学习系统误差的修正。 【实验原理】 物体在周期外力的持续作用下发生的振动称为受迫振动,这种周期性的外力称 为强迫力。如果外力是按简谐振动规律变化,那么稳定状态时的受迫振动也是简谐 振动,此时,振幅保持恒定,振幅的大小与强迫力的频率和原振动系统无阻尼时的 固有振动频率以及阻尼系数有关。在受迫振动状态下,系统除了受到强迫力的作用 外,同时还受到回复力和阻尼力的作用。所以在稳定状态时物体的位移、速度变化 与强迫力变化不是同相位的,存在一个相位差。当强迫力频率与系统的固有频率相 同时产生共振,此时振幅最大,相位差为90°。 实验采用摆轮在弹性力矩作用下自由摆动,在电磁阻尼力矩作用下作受迫振动 来研究受迫振动特性,可直观地显示机械振动中的一些物理现象。 当摆轮受到周期性强迫外力矩M=M,cOs©t的作用,并在有空气阻尼和电磁阻 尼的媒质中运动时(阻尼力矩为-b0)其运动方程为 dt -k0-b盟+M,osot (1) 式中,J为摆轮的转动惯量,-k0为弹性力矩,M,为强迫力矩的幅值,。为强迫 力的圆频率。 令,2-宁2邓=号m=号,则)式变为
13 实验三 受迫振动 在机械制造和建筑工程等科技领域中受迫振动所导致的共振现象引起工程技术 人员极大注意,既有破坏作用,但也有许多实用价值。众多电声器件是运用共振原 理设计制作的。此外,在微观科学研究中“共振”也是一种重要研究手段,例如利 用核磁共振和顺磁共振研究物质结构等。 表征受迫振动性质是受迫振动的振幅—频率特性和相位—频率特性(简称幅频 和相频特性)。 本实验中采用玻尔共振仪定量测定机械受迫振动的幅频特性和相频特性,并利 用频闪方法来测定动态的物理量—相位差。 【实验目的】 1. 研究玻尔共振仪中弹性摆轮受迫振动的幅频特性和相频特性。 2. 研究不同阻尼力矩对受迫振动的影响,观察共振现象。 3. 学习用频闪法测定运动物体的某些量,例相位差。 4. 学习系统误差的修正。 【实验原理】 物体在周期外力的持续作用下发生的振动称为受迫振动,这种周期性的外力称 为强迫力。如果外力是按简谐振动规律变化,那么稳定状态时的受迫振动也是简谐 振动,此时,振幅保持恒定,振幅的大小与强迫力的频率和原振动系统无阻尼时的 固有振动频率以及阻尼系数有关。在受迫振动状态下,系统除了受到强迫力的作用 外,同时还受到回复力和阻尼力的作用。所以在稳定状态时物体的位移、速度变化 与强迫力变化不是同相位的,存在一个相位差。当强迫力频率与系统的固有频率相 同时产生共振,此时振幅最大,相位差为 90°。 实验采用摆轮在弹性力矩作用下自由摆动,在电磁阻尼力矩作用下作受迫振动 来研究受迫振动特性,可直观地显示机械振动中的一些物理现象。 当摆轮受到周期性强迫外力矩 M M cos t = 0 的作用,并在有空气阻尼和电磁阻 尼的媒质中运动时(阻尼力矩为 dt d b − )其运动方程为 M cos t dt d k b dt d J 2 0 2 + = − − (1) 式中, J 为摆轮的转动惯量, − k 为弹性力矩, M0 为强迫力矩的幅值, 为强迫 力的圆频率。 令 J 2 k 0 = , J b 2 = , J m m 0 = ,则(1)式变为
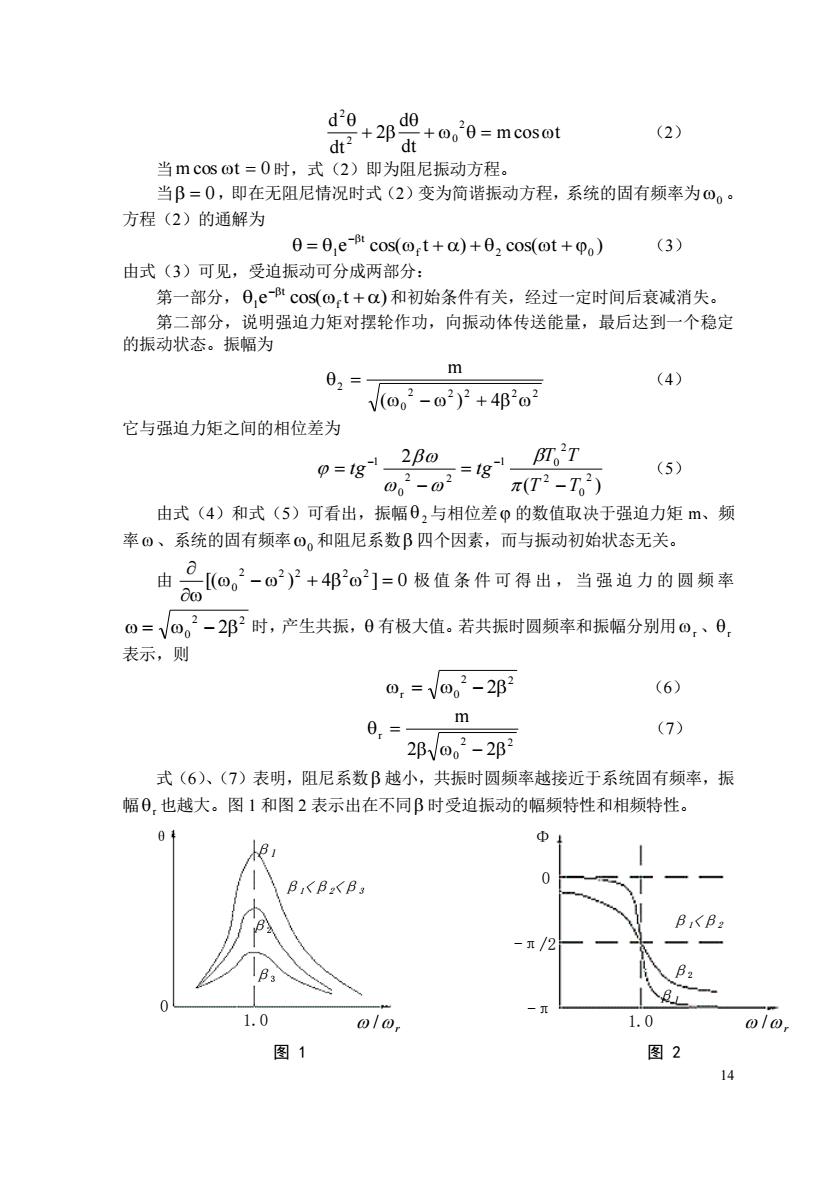
(2) dt 当m cos ot=0时,式(2)即为阻尼振动方程。 当B=0,即在无阻尼情况时式(2)变为简谐振动方程,系统的固有频率为O0· 方程(2)的通解为 日=日,ecos(ot+a)+02cos(ot+po) (3) 由式(3)可见,受迫振动可分成两部分: 第一部分,0,ecos(ot+a)和初始条件有关,经过一定时间后衰减消失。 第二部分,说明强迫力矩对摆轮作功,向振动体传送能量,最后达到一个稳定 的振动状态。振幅为 m 02 (4) V@,2-02y2+4B20 它与强迫力矩之间的相位差为 0,2-02*gm7 0=g12B@ (5) π(T2-T。2) 由式(4)和式(5)可看出,振幅0,与相位差p的数值取决于强迫力矩m、频 率0、系统的固有频率⊙。和阻尼系数B四个因素,而与振动初始状态无关。 品a-+邦0-0极监条件可得出,当强边力的圆频车 由 0=√@。2-2邛2时,产生共振,0有极大值。若共振时圆频率和振幅分别用0,、0, 表示,则 0,=V0,2-2p1 (6) m 0.=- (7) 2邓V02-2B 式(6)、(7)表明,阻尼系数β越小,共振时圆频率越接近于系统固有频率,振 幅0,也越大。图1和图2表示出在不同B时受迫振动的幅频特性和相频特性。 Φ BB2B3 8<B 9 1.0 1.0 图1 图2 14
14 mcos t dt d 2 dt d 2 2 0 2 + = + (2) 当 mcos t = 0 时,式(2)即为阻尼振动方程。 当 = 0 ,即在无阻尼情况时式(2)变为简谐振动方程,系统的固有频率为 0 。 方程(2)的通解为 e cos( t ) cos( t ) f 2 0 t = 1 + + + − (3) 由式(3)可见,受迫振动可分成两部分: 第一部分, e cos( t ) f t 1 + − 和初始条件有关,经过一定时间后衰减消失。 第二部分,说明强迫力矩对摆轮作功,向振动体传送能量,最后达到一个稳定 的振动状态。振幅为 2 2 2 2 2 0 2 ( ) 4 m − + = (4) 它与强迫力矩之间的相位差为 ( ) 2 2 0 2 2 1 0 2 2 0 1 T T T T tg tg − = − = − − (5) 由式(4)和式(5)可看出,振幅 2 与相位差 的数值取决于强迫力矩 m、频 率 、系统的固有频率 0 和阻尼系数 四个因素,而与振动初始状态无关。 由 [( ) 4 ] 0 2 2 2 2 2 0 − + = 极 值 条 件 可 得 出 , 当 强 迫 力 的 圆 频 率 2 2 = 0 − 2 时,产生共振, 有极大值。若共振时圆频率和振幅分别用 r 、r 表示,则 2 2 r = 0 − 2 (6) 2 2 0 r 2 2 m − = (7) 式(6)、(7)表明,阻尼系数 越小,共振时圆频率越接近于系统固有频率,振 幅 r 也越大。图 1 和图 2 表示出在不同 时受迫振动的幅频特性和相频特性。 图 1 图 2 r / β1 β2 β1<β2 -π -π/2 0 Φ 1.0 β1 β2 β3 β1<β2<β3 r 1.0 / θ 0