
二、D、E、P三矢量之间关系 85R}n0-cE p=,(e.-1)E 有电介质存在时的高斯定理的应用 (1)分析自由电荷分布的对称性,选择适当的高斯面 求出电位移矢量。 (2)根据电位移矢量与电场的关系,求出电场。 (3)根据电极化强度与电场的关系,求出电极化强度。 (4)根据束缚电荷与电极化强度关系,求出束缚电荷。 让美觉返司退
上页 下页 返回 退出 D E P = 0 + P E ( 1) = 0 r − D E E = = 0 r 有电介质存在时的高斯定理的应用 (1)分析自由电荷分布的对称性,选择适当的高斯面 求出电位移矢量。 (2)根据电位移矢量与电场的关系,求出电场。 (3)根据电极化强度与电场的关系,求出电极化强度。 (4)根据束缚电荷与电极化强度关系,求出束缚电荷。 二、 D E P 三矢量之间关系 、
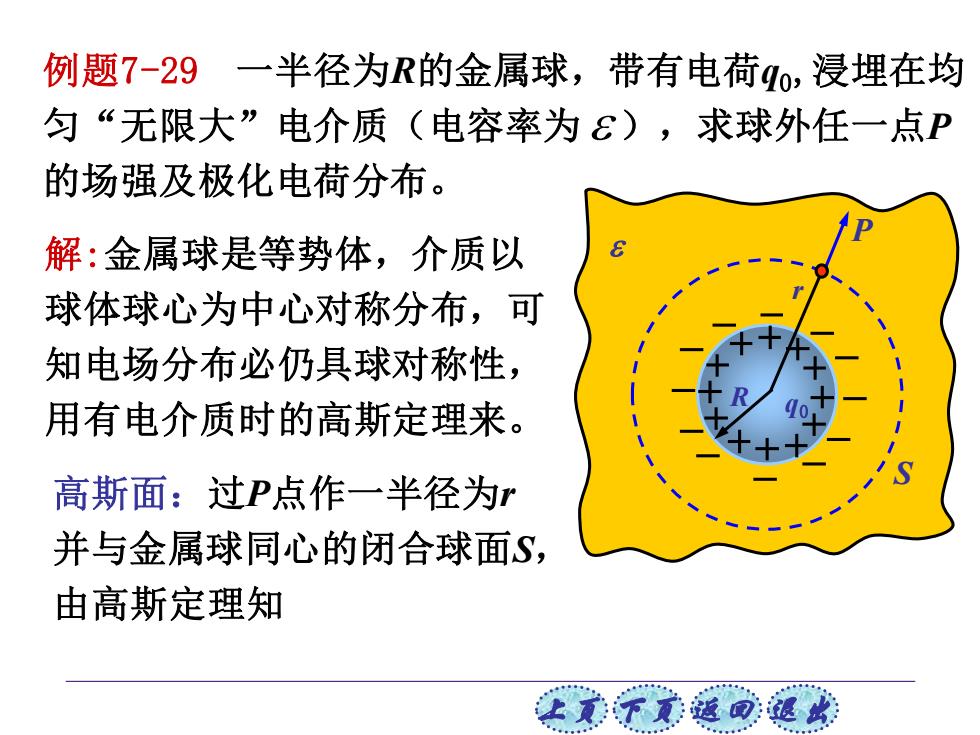
例题7-29一半径为R的金属球,带有电荷q0,浸埋在均 匀“无限大”电介质(电容率为E),求球外任一点P 的场强及极化电荷分布。 解:金属球是等势体,介质以 球体球心为中心对称分布,可 知电场分布必仍具球对称性, 用有电介质时的高斯定理来。 高斯面:过P点作一半径为 并与金属球同心的闭合球面S, 由高斯定理知 上贰不觉返回退此
上页 下页 返回 退出 例题7-29 一半径为R的金属球,带有电荷q0,浸埋在均 匀“无限大”电介质(电容率为 ),求球外任一点P 的场强及极化电荷分布。 解:金属球是等势体,介质以 球体球心为中心对称分布,可 知电场分布必仍具球对称性, 用有电介质时的高斯定理来。 R q0 r P S 高斯面:过P点作一半径为r 并与金属球同心的闭合球面S, 由高斯定理知