9 +音 一 维单原子链的o~q关系。这一关系我们 称为色散关系
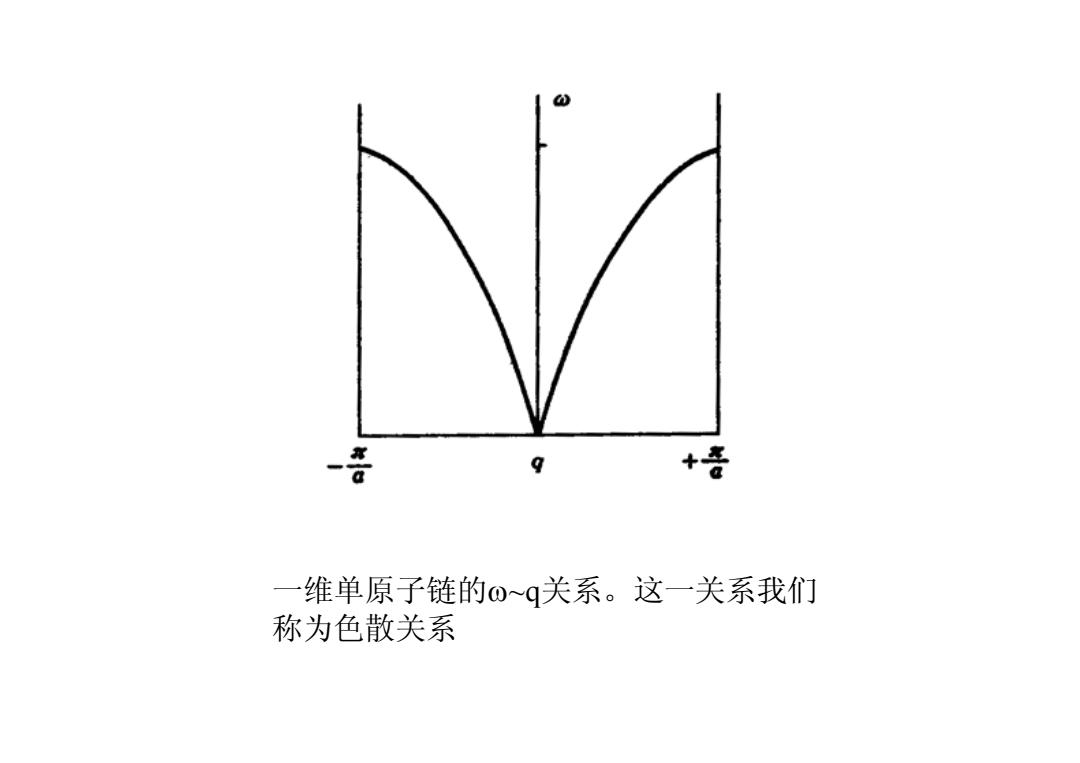
一维单原子链的ω~q关系。这一关系我们 称为色散关系
二、格波的简约性质、简约区 B o(q) 0=21 ”<q π 简约区 在简约区内,o与q一一对应, 称为q的主值范围。 -r/aq0π/aq 格波:Aeo-nag) 连续介质弹性波:Aeor-q) 格波:晶体中所有原子共同参与的一种频率相同的振动, 不同原子间有振动位相差,这种振动以波的形式在 整个晶体中传播,称为格波
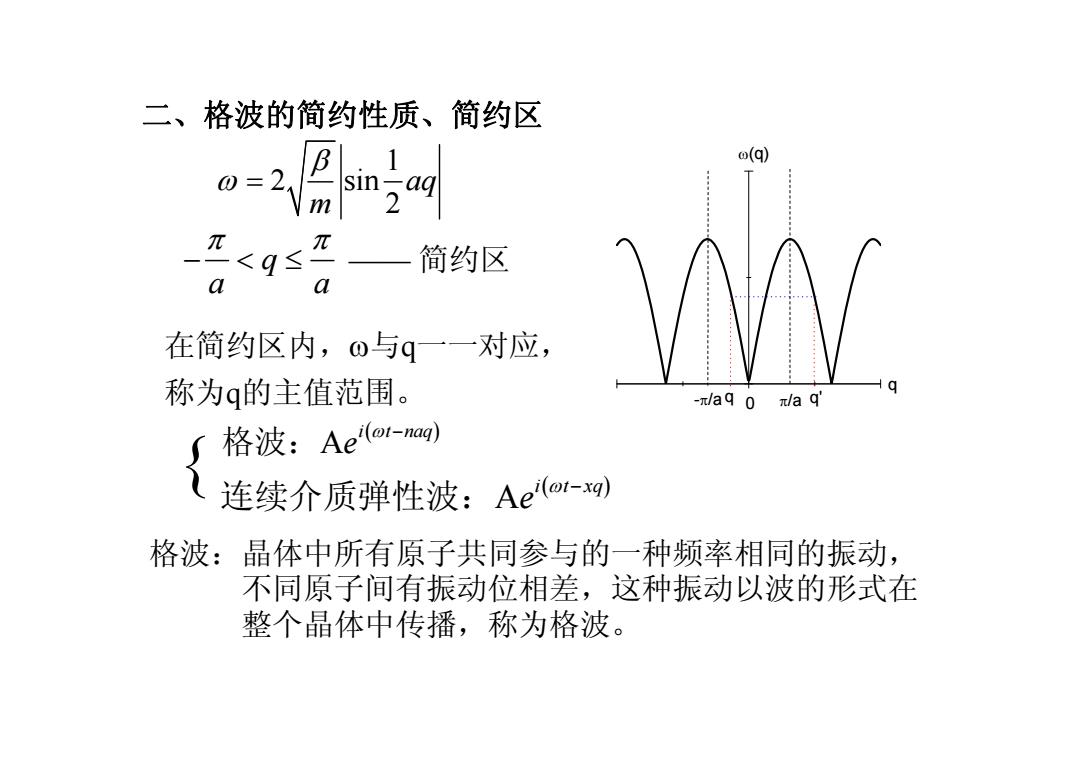
二、格波的简约性质、简约区 1 2 sin 2 aq m β ω = q a a π π − < ≤ —— 简约区 ( ) A i t naq e 格波: ω − ( ) A i t xq e 连续介质弹性波: ω − q q' 0 q ω(q) -π/a π/a 在简约区内, ω 与 q一一对应, 称为 q的主值范围。 { 格波:晶体中所有原子共同参与的一种频率相同的振动, 不同原子间有振动位相差,这种振动以波的形式在 整个晶体中传播,称为格波
从形式上看,格波与连续介质弹性波完全类似,但连续 介质弹性波中x是可以连续取值的;而在格波中只能取na (即原子的位置),这是一系列周期排列的点。由此可 知,一个格波解表示所有原子同时做频率为©的振动,不 同原子有不同的振动位相,相邻两原子的振动位相差为 ag。若ag改变2π的整数倍,这两个格波所描述的所有原 子的振动状态完全相同。 入=4a,即q1=2π/入1=元/2a; 2=4a/5,即q2=2π/2=5π/2a 2a q2q2=2π/a a 由图可以看出,由q,和q2所确定 的各原子的相对位置是完全相同 的,即这两个波数描述同一晶格 振动状态。因此,我们只需要q的 一个有限区间就能把所有的振动完全描述
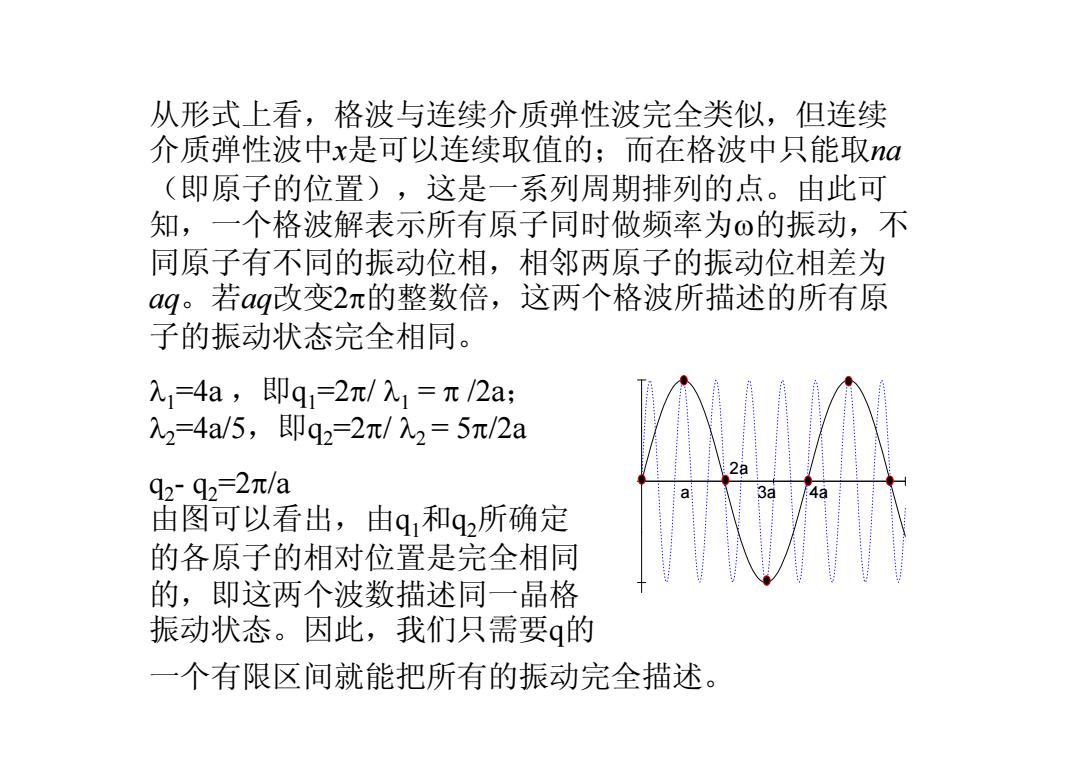
3a 4a 2a a 从形式上看,格波与连续介质弹性波完全类似,但连续 介质弹性波中x是可以连续取值的;而在格波中只能取na (即原子的位置),这是一系列周期排列的点。由此可 知,一个格波解表示所有原子同时做频率为ω的振动,不 同原子有不同的振动位相,相邻两原子的振动位相差为 aq。若aq改变2π的整数倍,这两个格波所描述的所有原 子的振动状态完全相同。 λ1=4a ,即q1=2π/ λ1 = π /2a; λ2=4a/5,即q2=2π/ λ2 = 5π/2a q2- q2=2π/a 由图可以看出,由q1和q2所确定 的各原子的相对位置是完全相同 的,即这两个波数描述同一晶格 振动状态。因此,我们只需要q的 一个有限区间就能把所有的振动完全描述

三、周期性边界条件(Born一Karman边界条件) 设晶体中原子总数为N,晶体链长为Na,所谓周期性 边界条件就是将一有限长度的晶体链看成无限长晶体链的 一个重复单元,即: N+1 ●● ●●● 12 n NN+2 N+n L= Aeo-w+nml=Aeo-ag) 即:ea=1 2.h :.q=Na h=整数
三、周期性边界条件(Born-Karman边界条件) μ N +n = μn 设晶体中原子总数为N,晶体链长为Na,所谓周期性 边界条件就是将一有限长度的晶体链看成无限长晶体链的 一个重复单元,即: 1 2 n N N+1 N+2 N+n i[ ] t ( ) N n nq i ( ) t naq Ae Ae − + − = ω ω =1 − iNaq 即:e h Na ∴q = ⋅ 2π h =整数

品经H价 一维链的玻恩~卡曼边界条件 我们可以把周期性边界条件看成是,在晶体链长Na很 大情况下,一条有限长度的晶体链首尾相接形成的边界条 件
我们可以把周期性边界条件看成是,在晶体链长Na 很 大情况下,一条有限长度的晶体链首尾相接形成的边界条 件