
第三与生去 [s-得 (6) 产物生成速率应该取决于中间产物浓度和相应反应速率常数,即 V=kx[ES] 代人式(6)得 (7) 当底物浓度很高时,酶被底物饱和,相当于所有的酶都和底物结合,即中间产物浓度[S]=酶的总 浓度[E],则反应达最大速率。即 V=k×[ES]=k2x[E] (8) 将式(8)代入(7),即得酶促反应的动力学方程为 得 (9) 这是1913年德国化学家Leonor Michaelis和Maud Menten提出的酶促反应动力学方程(经过后续完 普才成为式(9)的形式),即著名的Michaelis-Menten方程,简称米氏方程或米-曼方程。其中V为最大 反应速率,与酶的总浓度成正比例,K为米氏常数,[S]为底物浓度,V是不同[$]对应的酶促反应初 速率。 当底物浓度很低时([S]≤0.1×K),方程式分母中的[S]可忽略不计,米氏方程可简化成 V/K是与底物浓度无关的常数。所以,底物浓度足够低时,酶反应初速率与底物浓度成正比。 此正比关系可用于动力学法测定酶的底物量。 当底物浓度很高([S]≥10xK)时,方程式分母中的K可忽略不计,米氏方程可简化成V=V,反 应速率达到最大速率,再增加底物浓度也不再影响反应速率,即酶被底物饱和。 实践证实,绝大多数酶的动力学行为都可以用米氏方程描述,但也有特殊酶的动力学特点与此明显 不同。动力学行为可以用米氏方程描述的酶又称为米氏酶。 (二)米氏方程中动力学参数的意义 1.K值等于酶促反应速率为最大反应速率一半时的底物浓度当反应初速率为最大反应速率 半时,米氏方程为: 经整理得K=[S]。可见,K数值上等于酶促反应速率为最大反应速率一半时的底物浓度,相当于 维持酶活性中心有50%比例被底物结合时所需的底物浓度。 2.K值在一定条件下可用来表示酶对底物的亲和力由于K。=(k2+k)/k,故当k1>,即反 应达到稳态后,ES解离成E和S的速率远超过其分解成E和P的速率时,k对计算K的贡献可忽略不 计。按稳态反应的条件,此时K值应近似等于ES的解离常数K。 K.-[ESI-k. ES] 57

第一篇生物大分子的结构与功能 在这种情况下,K值可用来表示酶对底物的亲和力。K值愈大,则酶对底物的亲和力越小,这表示 需要很高浓度的底物才能使酶促反应达到最大反应速率。K值愈小,则酶与底物的亲和力愈高,这表 示不需要很高的底物浓度便可容易地到最大反应谏率。但并非所有酶促反应中k,值都远小于k,所 以,K,值和K值涵义不同,不能互相代替使用。 3.值是酶的特征常数之一K是醒对其底物的特征常数,与酶自身的结构、底物结构、反应环境 (如温度、pH、离子强度)有关,而与酶浓度无关。各种酶的K值分布范围很宽,多在106~102mo/ 之间。对于相同底物,不同的可能有不同的值:相同的酶,对于不同底物也可能有不同的值。 4.V,是酶完全被底物饱和时的反应速率V是最大反应速率,即酶完全被底物饱和时的反应速 率。V与酶浓度成正比关系,而与底物浓度无关。 加果酿浓度已知.可从V计算ES复合物分解生成产物的速率常数(k,)。例如.10 mmol/L的碳 酸酐酶溶液可在一秒钟内催化C0,与水反应生成0.6mol/LH,C0,则每秒钟每1分子酶可催化生成6 10分子的H,C0,。 5.k,代表率的转换数k,代表酶的转换数,也称为催化常数(k),相当于酶被底物完全饱和后单 位时间内每个活性中心催化底物生成产物的分子数。大多数酶对生理底物的转换数在1~10/s之间 6.k,/K为酶的专一性常数酶专一性包含两方面内容,即选择特定的底物和生成特定的产物。k 和K组成的组合参数(多底物酶有另外的组合方式)可以反映单底物酶促反应这两方面的能力,常被称 为酶的专一性常数。:,/K可用于筛选所设计作用于某个特定底物的高效酶突变体。此组合参数还可 反映酶的催化效率,或酶与底物之间发生碰撞时可生成产物的有效碰撞频率。酶与底物之间碰撞速率 的上限是1010L/(ml·s)。k/K值越接近此上限,酶的催化效率越高。因此,测定k,/K可用来 比较酶的专一性和对不同底物的催化效率,有助于判断酶的生理底物。延胡索酸酶的k2/K为1.6×10 L/(ml·s),磷酸丙糖异构酶的k/K为2.4×103L/(ml·s),乙酰胆碱酯酶的k/K为1,5×10L/ (mol·s),它们的催化效率都非常高。 (三)酶动力学参数的测定 酶促反应的V对[S]作图呈双曲线,其图形为渐近线,很难准确测得酶促反应的V和K值。实验 测定V值也不可能使用过高的底物浓度,因为底物浓度受到其溶解度的限制,且底物浓度过高时,对 于某些酶易出现高浓度底物对酶活性的抑制作用。目前最常用的方法是将米氏方程进行种种变换,将 曲线改为直线作图,便可以准确求得酶促反应的V和K值。 L.Lineweaver-Buk作图法将米氏方程式两边取倒数得到对应的双倒数方程 1-Ky v-V.xIs]tv 以1/V对1/[S]作图(图39),可得一直线,其 UY 横轴截距为-1/K,纵轴截距为1/V,直线斜率为 K/。此即双倒数作图法或林-贝氏作图法,是测 定酶动力学参数最常用的数据转换方法。此作图法 除用于求得V和K值外,还可用于判断可逆性抑 制反应的类型。此方法对低浓度底物下初速率测定 误差很敏感。所用底物浓度成等比数列分布在K两 侧时所得参数才最可靠。 -V/K 2.Hanes-.Voolf作图法在上术双倒数方程两 图39 Lineweaver-Burk作图法(双倒数作图法】
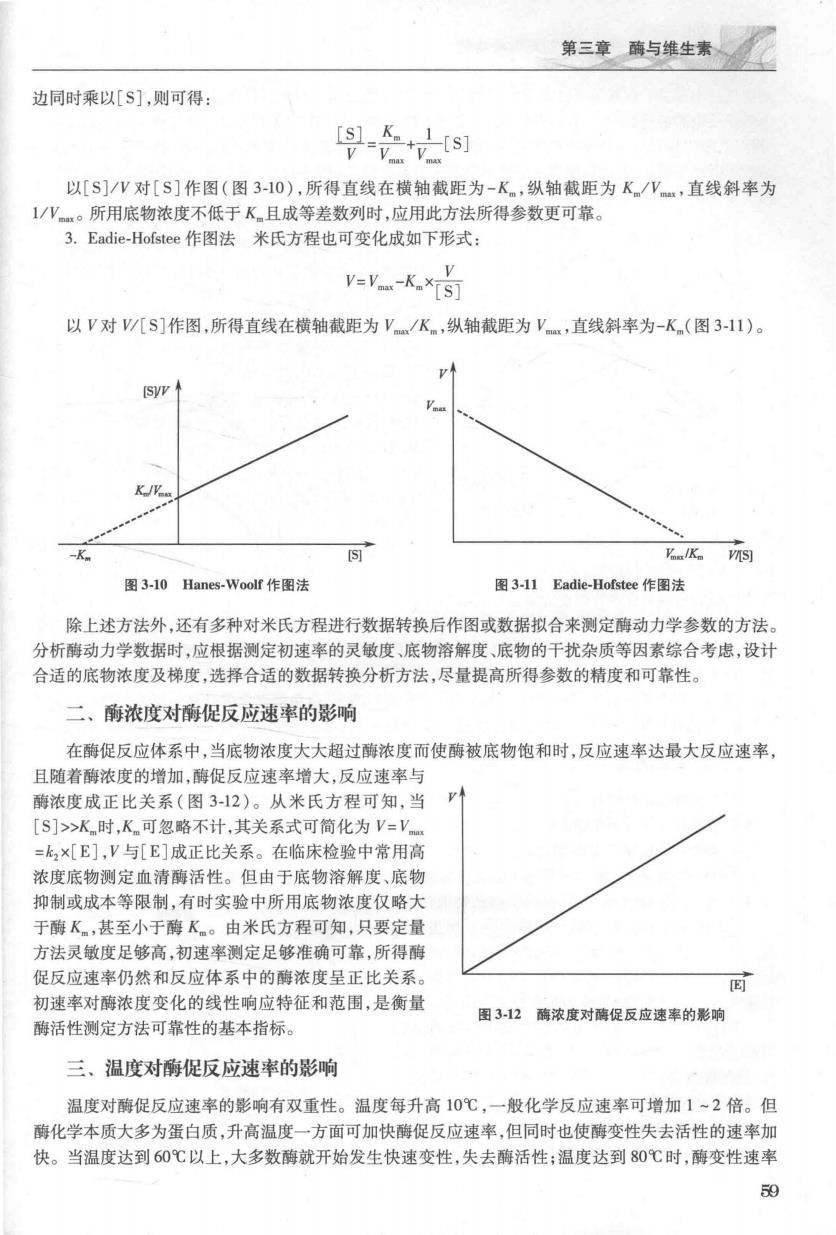
第三章与维生* 边同时乘以[S],则可得 以[S]/V对[S]作图(图3-10),所得直线在横轴截距为-K,纵轴截距为K/W,直线斜率为 ,所用底物浓度不低于K且成等差数列时,应用此方法所得参数更可靠 3.Eadie-Hofstee作图法米氏方程也可变化成如下形式: y=K×何 以V对/八S]作图,所得直线在横轴截距为V/K.,纵轴截距为V,直线斜率为-K(图3-11)。 K/V -K K。 图3-10 Hanes.Voolf作图法 图3-l1 Eadie-Hofstee作图法 除上述方法外,还有多种对米氏方程进行数据转换后作图或数据拟合来测定酶动力学参数的方法。 分析酶动力学数据时,应根据测定初速率的灵敏度、底物溶解度、底物的干扰杂质等因素综合考虑,设计 合适的底物浓度及梯度,选择合适的数据转换分析方法,尽量提高所得参数的精度和可靠性 二、酶浓度对衡促反应速率的影响 在酶促反应体系中,当底物浓度大大超过酶浓度而使酶被底物饱和时,反应速率达最大反应速率 且随着酶浓度的增加,酶促反应速率增大,反应速率与 酶浓度成正比关系(图3-12)。从米氏方程可知,当 [S]>K时,K可忽略不计,其关系式可简化为V=V =k×[E],V与[E]成正比关系。在临床检验中常用高 浓度底物测定血清酶活性。但由于底物溶解度、底物 抑制或成本等限制,有时实验中所用底物浓度仅略大 于酶K,甚至小于酶K。由米氏方程可知,只要定量 方法灵敏度足够高,初速率测定足够准确可靠,所得酶 促反应速率仍然和反应体系中的酶浓度呈正比关系。 E 初速率对酶浓度变化的线性响应特征和范围,是衡量 图3-12酶浓度对酶促反应速率的影响 活性测定方法可常性的基本指标。 三、温度对酶促反应速率的影响 温度对酶促反应速率的影响有双重性。温度每升高10℃,一般化学反应速率可增加1~2倍。但 酶化学本质大多为蛋白质,升高温度一方面可加快酶促反应速率,但同时也使酶变性失去活性的速率加 快。当温度达到60℃以上,大多数酶就开始发生快速变性,失去酶活性;温度达到80℃时,酶变性速率 59