3.2KCL和KVL的独立方程数 1.KCL的独立方程数 i1-i4-i6=0 ② -1-i2+i3=0 i2+is+i6=0 -i3+i4-i5=0 ①+②+③+④=0 结论 n个结点的电路,独立的KCL方程为n-1个。 上页 下页
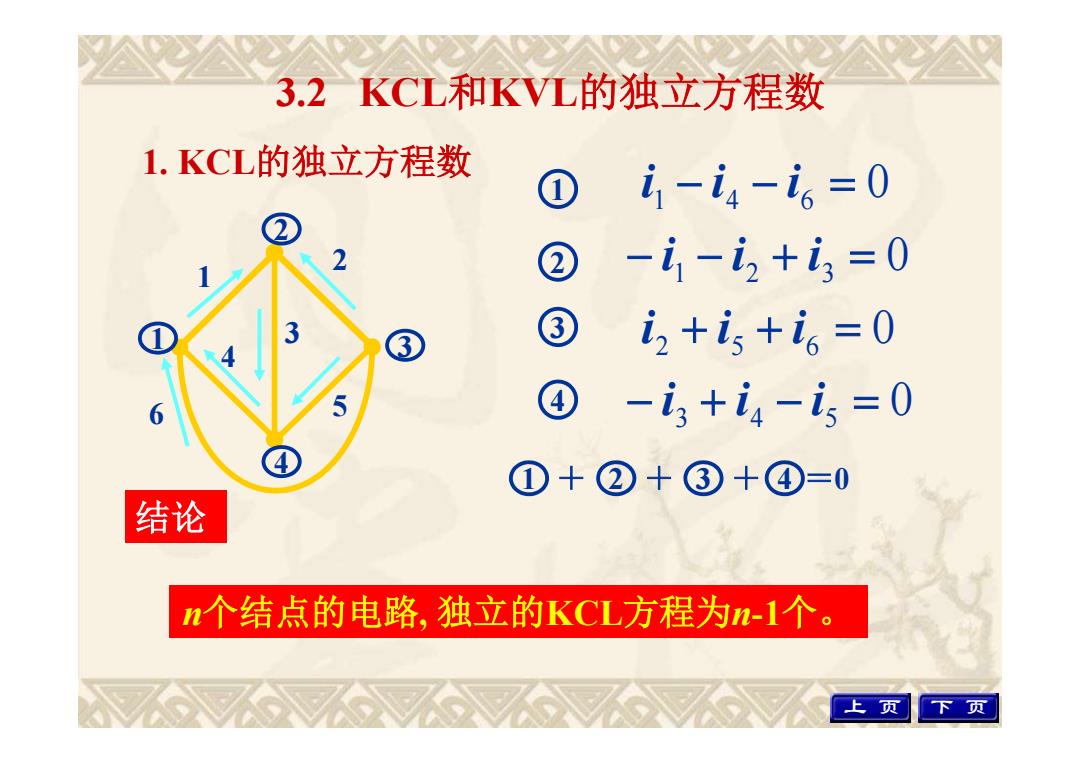
3.2 KCL和KVL的独立方程数 1. KCL的独立方程数 0 i1 i4 i6 6 5 4 3 2 1 4 3 2 1 1 4 3 2 0 i3 i4 i5 0 i2 i5 i6 0 i1 i2 i3 结论 n个结点的电路, 独立的KCL方程为n-1个。 上 页 下 页 1 + = 2 + +3 4 0

2.KVL的独立方程数 KVL的独立方程数=基本回路数=b一(n一1) 结论 n个结点、b条支路的电路,独立的 KCL和VL方程数为: (n-1)+b-(n-1)=b 上页 下页
2.KVL的独立方程数 KVL的独立方程数 = 基本回路数=b-(n-1) 结 论 n个结点、b条支路的电路, 独立的 KCL和KVL方程数为: (n 1) b (n 1) b 上 页 下 页

3.3支路电流法(Branch Current Method 1.支路电流法 以各支路电流为未知量列写电路方 程分析电路的方法。 对于有个节点、b条支路的电路,要求解支路电 流,未知量共有b个。只要列出b个独立的电路方程, 便可以求解这b个变量。 2.独立方程的列写 (1)从电路的n个结点中任意选择n-1个结点列写KCL方程 (2)选择基本回路列写b-(-1)个KVL方程 上页 下页
3.3 支路电流法(Branch Current Method) 对于有n个节点、b条支路的电路,要求解支路电 流,未知量共有b个。只要列出b个独立的电路方程, 便可以求解这b个变量。 以各支路电流为未知量列写电路方 程分析电路的方法。 1. 支路电流法 2. 独立方程的列写 (1)从电路的n个结点中任意选择n-1个结点列写KCL方程 (2)选择基本回路列写 b-(n-1) 个KVL方程 上 页 下 页
例 有6个支路电流,需列写6个方程 KCL方程: i1+i2-i6=0 -2+3+i4=0 -i4-i5+6=0 取网孔为基本回路,沿顺时 针方向绕行列KVL写方程: R6 回路1 R22+R33-Ri1=0 回路2 Rai-Rsis-Rsis =0 回路3」 R i+Rsis Rois us 上页 下页
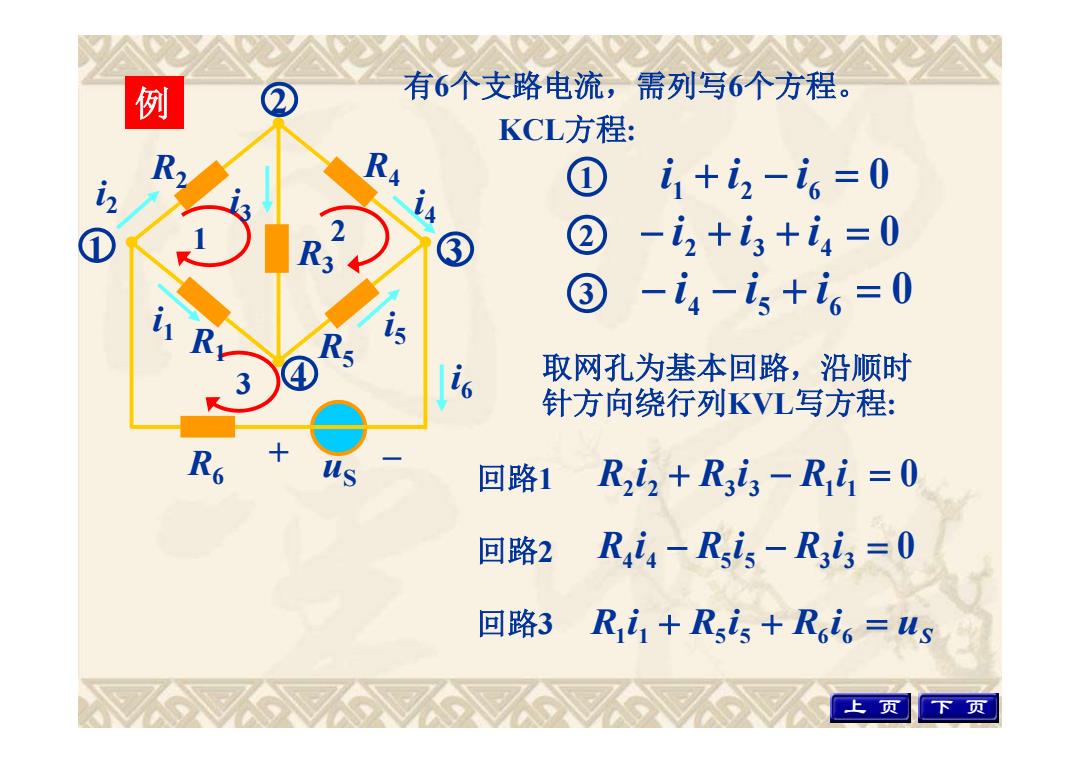
例 0 1 i1 i2 i6 3 2 0 i4 i5 i6 0 i2 i3 i4 有6个支路电流,需列写6个方程。 取网孔为基本回路,沿顺时 针方向绕行列KVL写方程: 0 R2 i2 R3 i3 R1 i1 0 R4 i4 R5 i5 R3 i3 uS R1 i1 R5 i5 R6 i6 回路1 回路2 回路3 1 2 3 上 页 下 页 R1 R2 R3 R4 R5 R6 + – i2 i3 i4 i1 i5 i6 uS 1 2 3 4 KCL方程:

支路电流法的一般步骤 ()标定各支路电流的参考方向; (2)选定(-1)个节点,列写其KCL方程; (3)选定b-(n-1)个独立回路,列写其KVL方程; (4)求解上述方程,得到b个支路电流; (⑤)进一步计算支路电压和进行其它分析。 支路电流法的特点 支路法列写的是KCL和KVL方程,) 所以方程列写 方便、直观,但方程数较多,宜于在支路数不多的情况 下使用。 上页 下页
支路电流法的一般步骤 (1) 标定各支路电流的参考方向; (2) 选定(n–1)个节点,列写其KCL方程; (3) 选定b–(n–1)个独立回路,列写其KVL方程; (4) 求解上述方程,得到b个支路电流; (5) 进一步计算支路电压和进行其它分析。 支路电流法的特点 支路法列写的是 KCL和KVL方程, 所以方程列写 方便、直观,但方程数较多,宜于在支路数不多的情况 下使用。 上 页 下 页