
一、用户的多归属倾向 考虑平台基于使用费展开的价格竞争 单归属于平台4的商家只能和愿意加入这个平台的消费者进行交易。这部分消费者的人数为D()。 ·如果某商家单归属于平台A,那么他可以得到的总剩余为: (u吃-p2)DA(p) ·如果商家多归属,那么消费者可以根据平台服务所带来的净效用选择在哪一个平台上进行交易。与对称价格情形相类似, 消费者选择平台A的前提条件是u≥p,且u-p1≥-p,而符合这些条件的消费者人数为d4(p,p)。其他满足条 件A≥pA,且-p>u一p1的消费者将选择平台B进行交易。这部分消费者的人数为d(p,p)。所以,如果某个商家 多归属,那么他能够实现的总剩余为: (u吃-pi)d(p,p)+(u吃-p)d(p,p) >结论:对于任意一个2≥的商家来说,单归属更好还是多归属更优,取决于以上两个总剩余的比较。 11
11 考虑平台基于使用费展开的价格竞争 一、用户的多归属倾向 单归属于平台A 的商家只能和愿意加入这个平台的消费者进行交易。这部分消费者的人数为𝐷1 𝐴 𝑝1 𝐴 。 • 如果某商家单归属于平台A,那么他可以得到的总剩余为: 𝑢2 𝐴 − 𝑝2 𝐴 𝐷1 𝐴 𝑝1 𝐴 • 如果商家多归属,那么消费者可以根据平台服务所带来的净效用选择在哪一个平台上进行交易。与对称价格情形相类似, 消费者选择平台A的前提条件是𝑢1 𝐴 ≥ 𝑝1 𝐴,且𝑢1 𝐴 − 𝑝1 𝐴 ≥ 𝑢1 𝐵 − 𝑝1 𝐵,而符合这些条件的消费者人数为𝑑1 𝐴 𝑝1 𝐴 , 𝑝1 𝐵 。其他满足条 件𝑢1 𝐴 ≥ 𝑝1 𝐴,且𝑢1 𝐵 − 𝑝1 𝐵 > 𝑢1 𝐴 − 𝑝1 𝐴的消费者将选择平台B进行交易。这部分消费者的人数为𝑑1 𝐵 𝑝1 𝐴 , 𝑝1 𝐵 。所以,如果某个商家 多归属,那么他能够实现的总剩余为: 𝑢2 𝐴 − 𝑝2 𝐴 𝑑1 𝐴 𝑝1 𝐴 , 𝑝1 𝐵 + 𝑢2 𝐵 − 𝑝2 𝐵 𝑑1 𝐵 𝑝1 𝐴 , 𝑝1 𝐵 ➢ 结论:对于任意一个𝑢2 ≥ 𝑝2 𝐵的商家来说,单归属更好还是多归属更优,取决于以上两个总剩余的比较

一、用户的多归属倾向 考虑平台基于使用费展开的价格竞争 给定<p,对任意一个商家来说,单归属于平台4时,单次交易的净剩余更高,但是总交易量更少。 ·对于最终选择多归属的商家来说,下面的不等式必须成立: (u吃-p)d(p,p)+((u吃-p)d明(p,p)≥(u吃-p)D(p) ·求解这个不等式可以得到: ≥吃-0=, d-(DA-dA) ·通过检查iz对偏导的符号可以发现,当平台A降低对商家的收费时,临界点12会上升: ∂t2 d Op a+d-p4<0 =1- 2
12 考虑平台基于使用费展开的价格竞争 一、用户的多归属倾向 给定𝑝2 𝐴 < 𝑝2 𝐵,对任意一个商家来说,单归属于平台A时,单次交易的净剩余更高,但是总交易量更少。 • 对于最终选择多归属的商家来说,下面的不等式必须成立: 𝑢2 𝐴 − 𝑝2 𝐴 𝑑1 𝐴 𝑝1 𝐴 , 𝑝1 𝐵 + 𝑢2 𝐵 − 𝑝2 𝐵 𝑑1 𝐵 𝑝1 𝐴 , 𝑝1 𝐵 ≥ 𝑢2 𝐴 − 𝑝2 𝐴 𝐷1 𝐴 𝑝1 𝐴 • 求解这个不等式可以得到: 𝑢2 ≥ 𝑝2 𝐵 𝑑1 𝐵 − 𝑝2 𝐴 𝐷1 𝐴 − 𝑑1 𝐴 𝑑1 𝐵 − 𝐷1 𝐴 − 𝑑1 𝐴 ≡ 𝑢ො2 • 通过检查𝑢ො2对𝑝2 𝐴偏导的符号可以发现,当平台A降低对商家的收费时,临界点𝑢ො2会上升: 𝜕𝑢ො2 𝜕𝑝2 𝐴 = 1 − 𝑑1 𝐵 𝑑1 𝐵 + 𝑑1 𝐴 − 𝐷1 𝐴 < 0

一、用户的多归属倾向 考虑平台基于使用费展开的价格竞争 >可定义一个消费者对平台B的单归属指数: 0B≡ d+dD d 这个指数衡量了当商家离开平台B时,会停止使用该平台的消费者比重。 13
13 考虑平台基于使用费展开的价格竞争 一、用户的多归属倾向 ➢ 可定义一个消费者对平台B的单归属指数: 𝜎𝐵 ≡ 𝑑1 𝐵 + 𝑑1 𝐴 − 𝐷1 𝐴 𝑑1 𝐵 • 这个指数衡量了当商家离开平台B时,会停止使用该平台的消费者比重
二、 平台竞争下的使用费定价 考虑平台基于使用费展开的价格竞争 根据之前的分析,当p疗≤p时,满足u2≥1z的商家将多归属于两个平台。这部分商家的数量为D2(2)=Pr(2≥2)。愿 意通过平台4与这部分商家进行交易的消费者人数为d(p,p)。满足条件2>u2≥p的商家将单归属于平台A。他们的数 量为D(@2)-D(p)。消费者如想与这些商家交易,就只能选择平台A。这部分消费者必须满足u≥p,他们的人数为 D(p). ·因此,平台A上所能产生的预期交易量为: QA(pi.p)=df(pi.p)D(a2)+DA(p)[D (p2)-D(2)] 2 好 D2以)D吐(z D(p吃)D(") 商家人数 14 图3.2降价对平台上商家人数的影响
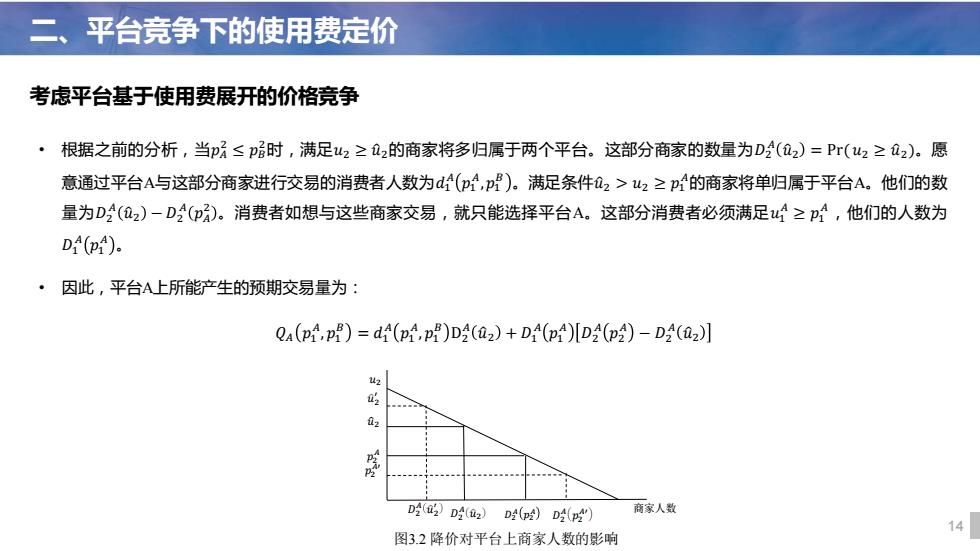
14 考虑平台基于使用费展开的价格竞争 二、平台竞争下的使用费定价 • 根据之前的分析,当𝑝𝐴 2 ≤ 𝑝𝐵 2时,满足𝑢2 ≥ 𝑢ො2的商家将多归属于两个平台。这部分商家的数量为𝐷2 𝐴 𝑢ො2 = Pr( 𝑢2 ≥ 𝑢ො2)。愿 意通过平台A与这部分商家进行交易的消费者人数为𝑑1 𝐴 𝑝1 𝐴 ,𝑝1 𝐵 。满足条件𝑢ො2 > 𝑢2 ≥ 𝑝1 𝐴的商家将单归属于平台A。他们的数 量为𝐷2 𝐴 𝑢ො2 − 𝐷2 𝐴 𝑝𝐴 2 。消费者如想与这些商家交易,就只能选择平台A。这部分消费者必须满足𝑢1 𝐴 ≥ 𝑝1 𝐴,他们的人数为 𝐷1 𝐴 𝑝1 𝐴 。 • 因此,平台A上所能产生的预期交易量为: 𝑄𝐴 𝑝1 𝐴 , 𝑝1 𝐵 = 𝑑1 𝐴 𝑝1 𝐴 , 𝑝1 𝐵 D2 𝐴 𝑢ො2 + 𝐷1 𝐴 𝑝1 𝐴 𝐷2 𝐴 𝑝2 𝐴 − 𝐷2 𝐴 𝑢ො2 𝑝2 𝐴 𝑢2 商家人数 𝐷2 𝐴 𝑝2 𝐴 图3.2 降价对平台上商家人数的影响 𝑢ො2 ′ 𝑝2 𝐴′ 𝑢ො2 𝐷2 𝐴 𝑢ො2 ′ 𝐷2 𝐴 𝑢ො2 𝐷2 𝐴 𝑝2 𝐴′

二、平台竞争下的使用费定价 考虑平台基于使用费展开的价格竞争 ·由平台A的需求,可以写出其利润最大化问题: =(+-c)(p ·上述最优化问题的一阶条件为: aA=0a+(f+吃-c小an 0A=0 op =Qa+(f+p哈-c)=0 15
15 考虑平台基于使用费展开的价格竞争 二、平台竞争下的使用费定价 • 由平台A的需求,可以写出其利润最大化问题: 𝑚𝑎𝑥 𝑝1 𝐴, 𝑝2 𝐴 𝜋𝐴 = 𝑝1 𝐴 + 𝑝2 𝐴 − 𝑐 𝑄𝐴 𝑝1 𝐴 , 𝑝1 𝐵 • 上述最优化问题的一阶条件为: 𝜕𝜋𝐴 𝜕𝑝1 𝐴 = 𝑄𝐴 + 𝑝1 𝐴 + 𝑝2 𝐴 − 𝑐 𝜕𝑄𝐴 𝜕𝑝1 𝐴 = 0 𝜕𝜋𝐴 𝜕𝑝2 𝐴 = 𝑄𝐴 + 𝑝1 𝐴 + 𝑝2 𝐴 − 𝑐 𝜕𝑄𝐴 𝜕𝑝2 𝐴 = 0