
20第二章逻辑代数基础 者所包含的物理意义有本质的不同。逻辑代数中也用字母表示变量,这种变量 称为逻辑变量。逻辑运算表示的是逻辑变量以及常量之间逻辑状态的推理运 算,而不是数量之间的运算。 虽然在二值逻辑中,每个变量的取值只有0和1两种可能,只能表示两种不 同的逻辑状态,但是我们可以用多变量的不同状态组合表示事物的多种逻辑状· 态,处理任何复杂的逻辑问题。 2.2逻辑代数中的三种基本运算 逻辑代数的基本运算有与(AND)、或(OR)、非(NOT)三种。为便于理解它 们的含义,先来看一个简单的例子。 图2.2.1中给出了三个指示灯的控制电路。在图(a)电路中,只有当两个 开关同时闭合时,指示灯才会亮:在图(b)电路中,只要有任何一个开关闭合,指 示灯就亮;而在图(©)电路中,开关断开时灯亮,开关闭合时灯反而不亮。 (3 6) 图2.2.1用于说明与、或、非定义的电路 如果把开关闭合作为条件(或导致事物结果的原因),把灯亮作为结果,那 么图2.2.1中的三个电路代表了三种不同的因果关系: 图()的例子表明,只有决定事物结果的全部条件同时具备时,结果才发 生。这种因果关系称为逻辑与,或称逻辑相乘。 图(b)的例子表明,在决定事物结果的诸条件中只要有任何一个满足,结果 就会发生。这种因果关系称为逻辑或,也称逻辑相加。 图(©)的例子表明,只要条件具备了,结果便不会发生;而条件不具备时,结 果一定发生。这种因果关系称为逻辑非,也称逻辑求反。 若以A、B表示开关的状态,并以1表示开关闭合,以0表示开关断开;以Y 表示指示灯的状态,并以1表示灯亮,以0表示不亮,则可以列出以0、1表示的 与、或、非逻辑关系的图表,如表2.2.1、表2.2.2和表2.2.3所示。这种图表称

2.2逻辑代数中的三种基本运算21 为逻辑真值表(truth table),简称真值表。 表2.2.1与逻相 表2.2.2或逻辑 表2.2.3非逻 运算的真值表 运算的真值表 运算的真值表 在逻辑代数中,将与、或、非看作是逻辑变量A、B间的三种最基本的逻辑运 算,并以“·”表示与运算,以“+”表示或运算,以变量右上角的“”表示非运算。 因此,A和B进行与逻辑运算时可写成 Y=A·B (2.2.1) A和B进行或逻辑运算时可写成 Y=A+B (2.2.2) 对A进行非逻辑运算时可写成 Y=A' (2.2.3) 同时,将实现与逻辑运算的单元电路称为与门,将实现或逻辑运算的单元电 路称为或门,将实现非逻辑运算的单元电路称为非门(也称为反相器)。 逻辑非的运算符号尚无统一的标准。除了本书中采用“”表示非运算以外 目前在国内、外的某些电子技术教材和EDA软件中,也采用A、~A、一A表示A 的非运算。用“”作为非运算符号比起在变量上加横线作为非运算符号更便于 计算机输人,尤其在逻辑运算式中存在多重非运算时,这种优越性就更加明显 因此,在教材和EDA软件中使用“”作为非运算符号的越来越多了。 与、或、非逻辑运算还可以用图形符号表示。图2.2.2中给出了被EEE(电 气与电子工程师协会)和EC(国际电工协会)认定的两套与、或、非的图形符 号,其中一套是目前在国外教材和EDA软件中普遍使用的特定外形符号,如图 2.2.2(a)所示。另一套是矩形轮廓的符号,如图2.2.2(b)所示。本书中采用特 定外形符号。 实际的逻辑问题往往比与、或、非复杂得多,不过它们都可以用与、或、非 的组合来实现。最常见的复合逻辑运算有与非(NAND)、或非(NOR)、与或非 (AND-NOR)、异或(EXCLUSIVE OR)、同或(EXCLUSIVE NOR)等。表 2.2.4~表2.2.8给出了这些复合逻辑运算的真值表。图2.2.3是它们的图 形逻辑符号和运算符号。这些图形符号同样也有特定外形符号和矩形轮廓

22第二章逻辑代数基础 符号两种。 4○-y4-y4>- 与 或 a) 日,巴?4巴- 或 ) 图2.2.2与、或、非的图形符号 (a)特定外形符号(b)矩形轮廓符号 表2.2.4与非逻辑的真值表 表2.2.5或非逻辑的真值表 A BY A BY 0 0 0 0 1 0 0 1 1 10 1 0 表2.2.6与或非逻辑的真值表 B D Y 表2.2.7异或逻辑的真值表 0 0 0 0 B 1 1 0 0 0 1 0 0 0 0 1 1 0 0 1 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 1 0 1 1 0 1 1 1 0 1 0 0 0 表2.2.8同或逻辑的真值表 1 0 0 1 1 A B 1 0 1 0 1 0 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 0 1 1 1 0
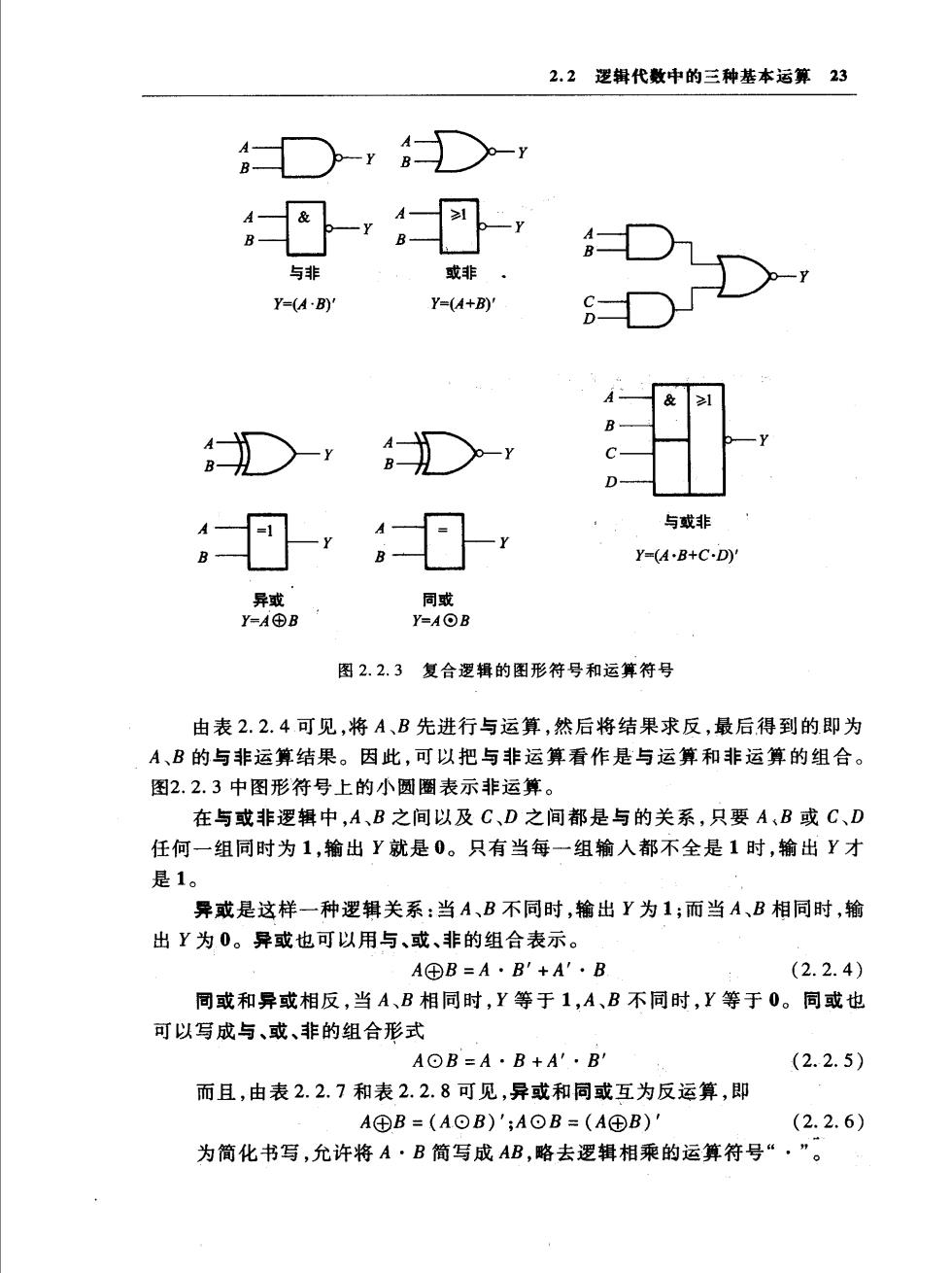
2.2逻辑代数中的三种基本运算23 ○-4D- 与非 或非 Y=(4B Y=(4+B)' 与或非 Y-(A-B+C-D) 图2.2.3复合逻辑的图形符号和运算符号 由表2.2.4可见,将A、B先进行与运算,然后将结果求反,最后得到的即为 A、B的与非运算结果。因此,可以把与非运算看作是与运算和非运算的组合。 图2.2.3中图形符号上的小圆圈表示非运算。 在与或非逻辑中,A、B之间以及C、D之间都是与的关系,只要A,B或C、D 任何一组同时为1,输出Y就是0。只有当每一组输人都不全是1时,输出Y才 是1。 异或是这样一种逻辑关系:当A、B不同时,输出Y为1;而当A、B相同时,输 出Y为0。异或也可以用与、或、非的组合表示。 A④B=A·B'+A'·B (2.2.4) 同或和异或相反,当A、B相同时,Y等于1,A、B不同时,Y等于0。同或也 可以写成与、或、非的组合形式 A⊙B=A·B+A'·B (2.2.5) 而且,由表2.2.7和表2.2.8可见,异或和同或互为反运算,即 A④B=(A⊙B)';A⊙B=(A⊕B)' (2.2.6) 为简化书写,允许将A·B简写成AB,略去逻辑相乘的运算符号

24第二章逐辑代数基础 复习思考题 R2.2.1你能各举出一个现实生活中存在的与、或、非逻辑关系的事例吗? 2.2.2两个变量的异或运算和同或运算之间是什么关系? 分分分分分分分y分心分分L分L分分分分分分分分L分分分分分分分分分L分分 2.3逻辑代数的基本公式和常用公式 2.3.1基本公式 表2.3.1给出了逻辑代数的基本公式。这些公式也称为布尔恒等式。 表2.3.1逻辑代数的基本公式 序号 公 序号 公 式 0·A=0 10 1'=0:0'=1 2 1·A=A 11 1+A=1 3 A·A=A 0+A=A A·A'=0 13 A+A=A A·B=B·A 14 A+A'=1 6 A·(B·C)=(A·B)·C 15 AR=RA A·(B+C)=A·B+A·C 16 A+(B+C)=(A+B)+C 8 (A·B)'=A'+B 17 A+B,C=(A+B)·(A+C) 9 (A')'=A 18 (A+B)'=A'·B 式(1)、(2)、(11)和(12)给出了变量与常量间的运算规则。 式(3)和(13)是同一变量的运算规律,也称为重叠律。 式(4)和(14)表示变量与它的反变量之间的运算规律,也称为互补律 式(5)和(15)为交换律,式(6)和(16)为结合律,式(7)和(17)为分配律。 式(8)和(18)是著名的德·摩根(De.Morgan)定理,亦称反演律。在逻辑 函数的化简和变换中经常要用到这一对公式。 式(9)表明,一个变量经过两次求反运算之后还原为其本身,所以该式又称 为还原律。 式(10)是对0和1求反运算的规则,它说明0和1互为求反的结果。 这些公式的正确性可以用列真值表的方法加以验证。如果等式成立,那么 将任何一组变量的取值代入公式两边所得的结果应该相等。因此,等式两边所