
1.5几种常用的编码15 中,如果最右边一位的变化比其他两位的变化慢,就会在一个极短的瞬间出现 0101状态,这个状态将成为转换过程中出现的噪声。而在第四行的格雷码0010 向第五行的0110转换过程中则不会出现过渡噪声。这种过渡噪声在有些情况 下甚至会影响电路的正常工作,这时就必须采取措施加以避免。在第4.4节中 我们还将进一步讨论这个问题。 十进制代码中的余3循环码就是取4位格雷码中的十个代码组成的,它仍 然具有格雷码的优点,即两个相邻代码之间仅有一位不同: 三、美国信息交换标准代码(ASCI) 美国信息交换标准代码(American Standard Code for Information Interchange. 简称ASCII码)是由美国国家标准化协会(ANSI)制定的一种信息代码,广泛地 用于计算机和通信领域中。ASCIⅡ码已经由国际标准化组织(IS0)认定为国际 通用的标准代码。 ASCI码是一组7位二进制代码(b,bb,b,b,b,b,),共128个,其中包括表示 0~9的十个代码,表示大、小写英文字母的52个代码,32个表示各种符号的代 码以及34个控制码。表1.5.3是ASCⅡ码的编码表,每个控制码在计算机操作 中的含义列于表1.5.4中。 表1.5.3美国信息交换标准代码(ASC码) b3babs 000 010 011 100 10u 110 111 0000 NUL DLE SP 0 @ 0001 SOH DCI 010 STX DC2 R 0011 ETX 3 010 EOT DC4 D 0101 ENQ NA 010 ACK SYN 0111 ETE 100 BS h 1001 EM 9 1010 LF J j 1011 S 10 F L 0 M 110 N 1111 SI US DEL
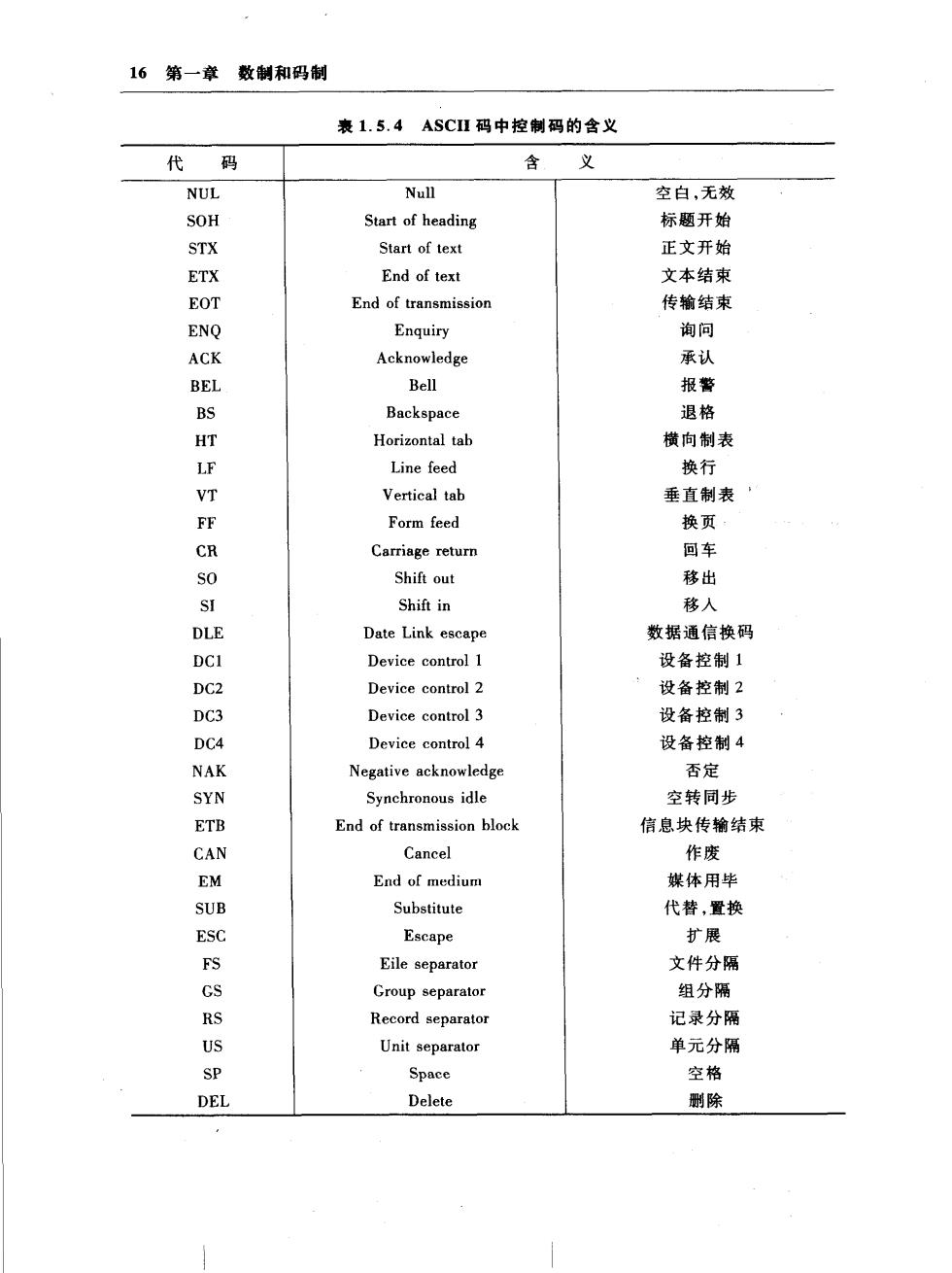
16第一章数制和码制 表1.5.4ASCⅡ码中控制码的含义 代码 含 义 NUL Null 空白,无效 SOH Start of heading 标题开始 STX Start of text 正文开始 ETX End of text 文本结束 EOT End of transmission 传输结束 ENQ Enquiry 询问 ACK Acknowledge 承认 BEL Bell 报警 BS Backspace 退格 Horizontal tab 横向制表 Line feed 换行 Vertical tab 垂直制表 Form feed 换页 Carriage return 回车 s0 Shift out 移出 Shift in 移人 DLE Date Link escape 数据通信换码 DCI Device control 1 设备控制1 DC2 Device control2 设备控制2 DC3 Device control 3 设备控制3 DC4 Device control 4 设备控制4 NAK Negative acknowledge 否定 SYN Synchronous idle 空转同步 ETB End of transmission block 信息块传输结東 CAN Cancel】 作废 EM End of medium 媒体用毕 SUB Substitute 代替,置换 ESC Escape 扩展 Eile separator 文件分隔 Group separator 组分隔 Record separator 记录分隔 US Unit separator 单元分隔 SP Space 空格 DEL Delete 删除

城9w海习名题17 复习思考题 R1.5.18421码、2421码5211码、余3码和余3循环码在编码规则上各有何特点? 1.5.2你能写出3位和5位格雷码的顺序编码吗? R1.5.3你能用ASCl代码写出“Well Come!”吗? 本章小结 不同的数码既可以用来表示不同数量的大小,又可以用来表示不同的事物。 在用数码表示数量的大小时,采用的各种计数进位制规则称为数制。常用 的数制有十进制、二进制、八进制和十六进制几种。各种进制所表示的数值可以 按照本章介绍的方法互相转换。 由于数字电路的基本运算都采用二进制运算,所以这一章里还比较详细地 介绍了二进制数的符号在数字电路中的表示方法,原码、反码和补码的概念,以 及采用补码进行带符号数加法运算的原理。 在用数码表示不同的事物时,这些数码巴没有数量大小的含义,所以将它们 称为代码。本章中所列举的十进制代码、格雷码、ASCI码是几种常见的通用代 码。此外,我们完全可以根据自己的需要,自行编制专用的代码。m世大 习题 00t 【题1.1】为了将600份文件顺序编码,如果采用二进制代码,最少需要用几位?如果 改用八进制或十六进制代码,则最少各需要用几位?行忙 【题1.2】将下列二进制整数转换为等值的十进制数。 (1)(01101)2:(2)(10100)2:+(3)(10010111)2;(4)(1101101)2。 【题1.3】将下列二进制小数转换为等值的十进制数。 (1)(0.1001)2:(2)(0.0111)2;(3)(0.101101)2: (4)(0.001111)2 【题1.4】将下列二进制数转换为等值的十进制数。 (1)(101.011)2;(2)(110.101)2;(3)(1111.1111)2: (4)(1001.0101)20 【题1.5】将下列二进制数转换为等值的八进制数和十六进制数。 (1)(1110.0111)2:(2)(100L.1101)2(3)(0110.1001)2;(4)(101100.110011)2。 【题1.6】将下列十六进制数转换为等值的二进制数。 (1)(8C) (2)(3D.BE)6:(3)(8F.FF)6;(4)(10.00)6。 【题1.7】将下列十进制数转换为等值的二进制数和十六进制数

18第一章.数制和码制 (1)(17)n:(2)(127)。:(3)(79):(4)(255)0 【题1.8】将下列十进制数转换为等值的二进制数和十六进制数。要求二进制数保留 小数点以后8位有效数字。 (1)(0.519)。;(2)(0.251)o;(3)(0.0376)0:(4)(0.5128)o。 【题1.9】将下列十进制数转换为等值的二进制数和十六进制数。要求二进制数保留 小数点以后4位有效数字。 (1)(25.7)1o:(2)(188.875)10;(3)(107.39)0;(4)(174.06)10。 【题1.10】写出下列二进制数的原码、反码和补码。 (1)(+1011)2:(2)(+00110)2;(3)(-1101)2:(4)(-00101)20 【题1.1】写出下列带符号位二进制数(最高位为符号位)的反码和补码。 (1)(011011)2;(2)(001010)2:(3)(111011)2;(4)(101010)2。 【题1.12】用8位的二进制补码表示下列十进制数。 (1)+17;(2)+28;(3)-13;(4)±47;(5)-89;(6)-121。 【题1.13】计算下列用补码表示的二进制数的代数和。如果和为负数,请求出负数的 绝对值。 (1)01001101+00100110: (2)00011101+01001100: (3)00110010+10000011: (4)00011110+10011100: (5)11011101+01001011 (6)10011101+01100110 (7)11100111+11011011: (8)11111001+10001000。 【题1.14】用二进制补码运算计算下列各式。式中的4位二进制数是不带符号位的绝 对值。如果和为负数,请求出负数的绝对值。(提示:所用补码的有效位数应足够表示代数 和的最大绝对值。) (1)1010+0011 (2)1101+1011: (3)1010-0011: (4)1101-1011: (5)0011-1010; (6)1011-1101: (7)-0011-1010; (8)-1101-1011。 【题1.15】用二进制补码运算计算下列各式。(提示:所用补码的有效位数应足够表示 代数和的最大绝对值。) (1)3+15(2)8+11(3)12-7;(4)23-11: (5)9-12;(6)20-25;(7)-12-5;(8)-16-14

第二章 逻辑代数基础 燃丹卧 内容提要 本章介绍分析数字电路逻辑功能的数学方法。文中首先扼要地介绍了逻辑代数的墓 本公式、常用公式和重要定理,然后讲述迈辑函数及其表示方法,最后介绍如何应用这些 公式和定理化简逻辑函数,以及用计算机软件进行逻辑函数化简和变换的方法。 为便于读者理解和掌握这些公式、定理和方法,各部分均配置了一定数量的例题 2.1概述 在上一章中我们已经讲过,不同的数码不仅可以表示数量的不同大小, 而且还能用来表示不同的事物。在数字逻辑电路中,用1位二进制数码的0 和1表示一个事物的两种不同逻辑状态。例如,可以用1和0分别表示 件事情的是和非、真和伪、有和无、好和坏,或者表示电路的通和断、电灯的 亮和暗、门的开和关等等。这种只有两种对立逻辑状态的逻辑关系称为二 值逻辑。 所谓“逻辑”,在这里是指事物间的因果关系。当两个二进制数码表示不同 的逻辑状态时,它们之间可以按照指定的某种因果关系进行推理运算。我们将 这种运算称为逻辑运算。 ,1849年英国数学家乔治·布尔(George Boole)首先提出了进行逻辑运算的 数学方法一布尔代数。后来,由于布尔代数被广泛应用于解决开关电路和数 字逻辑电路的分析与设计中,所以也将布尔代数称为开关代数或逻辑代数。本 章所讲的逻辑代数就是布尔代数在二值逻辑电路中的应用。下面我们将会看 到,虽然有些逻辑代数的运算公式在形式上和普通代数的运算公式雷同,但是两