我们知道一个相量可以用复数表示 而正弦量又可以用相量表示,因此正弦量 可以用复数表示。 1.复数表示法 A=a+j b 代数式 A=r(cosy+j siny)三角式 根据欧拉公式: eio=cos o+jsin p +1 A=rejo 指数式 A=r∠W 极坐标式 BACK NEXT
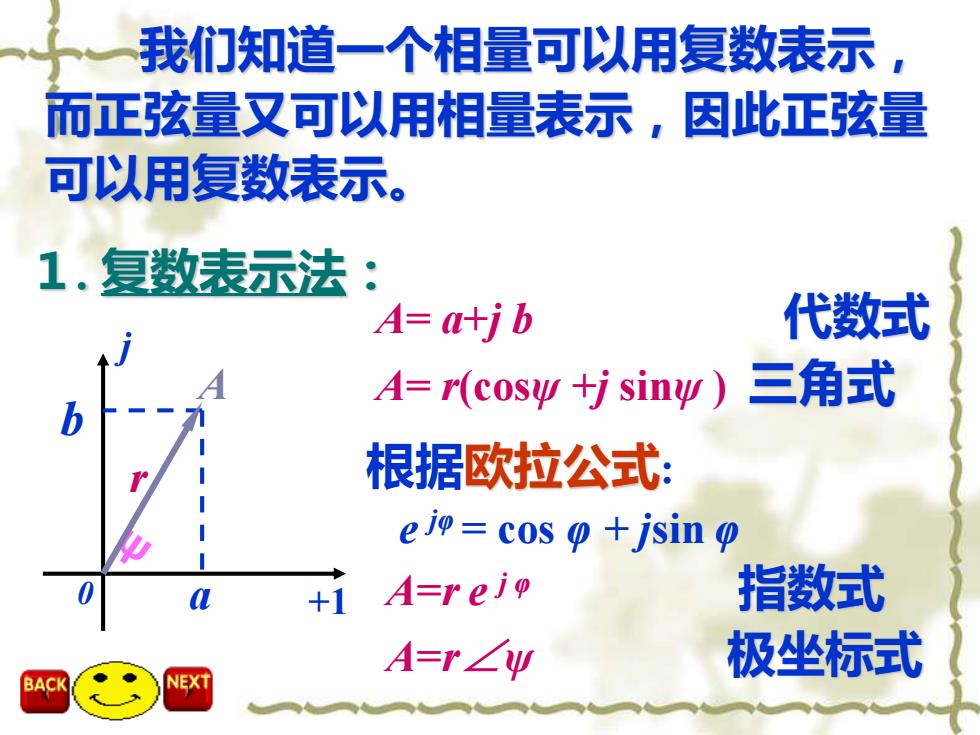
1. 复数表示法: a j b A 根据欧拉公式: e jφ = cos φ + jsin φ A=r e j φ 指数式 A=r∠ψ 极坐标式 我们知道一个相量可以用复数表示, 而正弦量又可以用相量表示,因此正弦量 可以用复数表示。 +1 0 r A= a+j b 代数式 A= r(cosψ +j sinψ ) 三角式

BACK NEXT 其中 ∫=r cosw b=r siny =√a2+b2 arctg b/a 2.正弦量的相量 一个复数的幅角等于正弦量的初相角 复数的模等于正弦量的最大值或有效值 该复数称为正弦量的相量
其中 ψ = arctg ( b/a ) 2 2 r = a + b a = r cosψ b = r sinψ 2. 正弦量的相量 一个复数的幅角等于正弦量的初相角, 复数的模等于正弦量的最大值或有效值, 该复数称为正弦量的相量

这样, 表示正弦电压u=V sin(ot+平) 的相量为 Unm=Ueiv=Um∠y 为了使计算结果能直接表示正弦量的有 效值,通常使相量的模等于正弦量的有效 值,即可以表示为: U=Uejw=U∠w BACK NEXT
这样,表示正弦电压 的相量为 u = U sin(t + ) m Um = Um e = Um j 为了使计算结果能直接表示正弦量的有 效值,通常使相量的模等于正弦量的有效 值,即可以表示为: U = Ue = U j

BACK NEXT 注意! (1)只有正弦量才能用相量表示; (2)几个同频率正弦量可以画在同一 相量图上: (3)任意两个同频率正弦量的和或差 可用平行四边形法则求; (4)正弦量的瞬时值=相量虚部 .u呋Um
(1)只有正弦量才能用相量表示; 注意! (2)几个同频率正弦量可以画在同一 相量图上; (3)任意两个同频率正弦量的和或差 可用平行四边形法则求; (4)正弦量的瞬时值=相量虚部 ∴ u≠Um

例3-2 已知i=10W2sin(ot+30)A i,=5V2sin(ot-60)A 试写出和i的表达式,并 画出其向量图。 解 i1和i,对应的电流向量 30 表达式分别为 +1 i1=10∠30°(A) i2=5∠-60(A) i的长度是i,的二倍。 BACK NEXT
30 -60 0 +j +1 已知 ( ) 5 2sin( 60 )A 10 2sin 30 A 2 1 = − = + i t i t 试写出 和 的表达式,并 画出其向量图。 2 I 1 I i1 和 i2 对应的电流向量 表达式分别为 ( ) 5 60 (A) 10 30 A 2 1 = − = I I I 1 的长度是 I 2 的二倍。 例3-2 1 解: I 2 I