
BACK NEXT 有效值与最大值的关系推导如下: 1-促1,.xint@t+婴,Pr =7221-os2o+平,a Jm≈0.707Lm /2
m m i T m T m i I I I t t T I t t T I 0.707 2 [1 cos 2( )]d 2 1 1 [ sin( )] d 1 0 2 2 0 = = − + = + 有效值与最大值的关系推导如下:

例3-1 已知i=msin(aot什元/6)A,0-314rad/s,t=0 时其瞬时值为16A。试求有效值I并求t 为多少时i=Im? In sin"=16 元 i=Im 即有 6 1Lm=32(A) 1。sin oot+) --a)(r+- ot+ 元 元 元 2 2 6 3 ≈0.00333(S)=3.33(ms BACK NEXT 314
已知i=Imsin(t+/6)A , =314rad/s , t=0 时其瞬时值为16A 。试求有效值 I 并求t 为多少时 i =Im? 16 6 π I m sin = 32(A) I m = 22 63(A) 2 1 I = I m . i =Im, 即有 6 2 1 6 sin 6 π m sin m + = = + = + t t I t I 0 00333(s) 3 33(ms) 314 3 π 6 π 2 π t = . = . − = 例3-1 解:

第三节 正弦量的相量表示法 正弦量的矢量表示法 正弦信号的三要素可用一旋转矢 量来表示: 令 矢量长度=Im 矢量初始角=少 矢量旋转速度=wω BACK NEXT
正弦信号的三要素可用一旋转矢 量来表示: 令 矢量长度=Im 矢量初始角=Ψ 矢量旋转速度=ω 第二节 正弦量的相量表示法 一、正弦量的矢量表示法
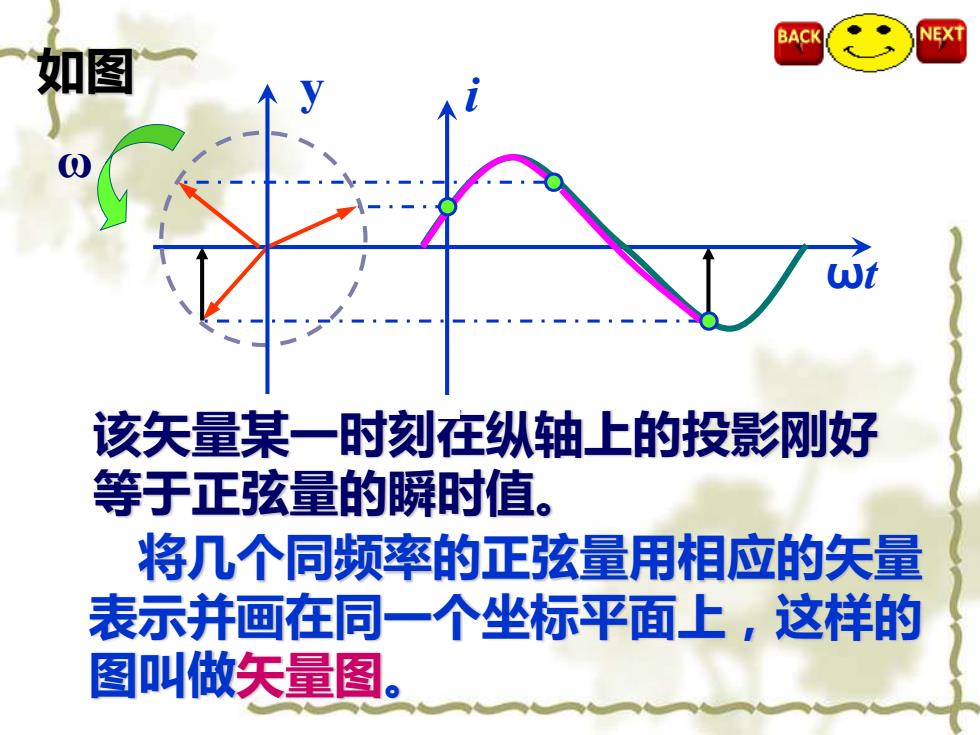
BACK NEXT 如图 ωt 该矢量某一时刻在纵轴上的投影刚好 等于正弦量的瞬时值。 将几个同频率的正弦量用相应的矢量 表示并画在同一个坐标平面上,这样的 图叫做矢量图
ω y i ω 如图 该矢量某一时刻在纵轴上的投影刚好 等于正弦量的瞬时值。 将几个同频率的正弦量用相应的矢量 表示并画在同一个坐标平面上,这样的 图叫做矢量图。 ωt

BACK NEXT 正弦量的相量表示法 般我们研究的是同频率的正弦量 用相量表示时,它们同以w速度旋转,相 对位置保持不变。因此,在同一相量图 中,以=0时刻的相量表示正弦量。 相量的写法为:大写字母的上方加一 个 199
一般我们研究的是同频率的正弦量, 用相量表示时,它们同以ω速度旋转,相 对位置保持不变。因此,在同一相量图 中,以t=0时刻的相量表示正弦量。 相量的写法为:大写字母的上方加一 个“. ” 。 二、正弦量的相量表示法