
9 g-I suonoos'gt lauueyp Ksiou e yiIM Sulpooap 'uollugoa ypaads (xxxee:uoneueldx!soW Sulujeal oj jenuassa 'sanens ised jo anewnsa janaq >00 ()d :Bulyoows aouapIna ay1 inoy Im gualyay!l :saouanbas uonpe ajqissod jo uolenjene 0<y0 (x)d :uonp!pald quage jeuone e yo ssaood uoisipap ayn on indul-anes jaljaq (oX)d:auua」 syse aouelojul
tasks Inference )t 1: e|t X( P: Filtering agent rational a of cess ro p decision the to —input state elief b 0 >kr fo )t 1: e| k +t X( P: Prediction sequences; action ossible p of evaluation evidence the without filtering e lik t <k ≤0 r fo )t 1: e| k X( P: othing Smo rning lea r fo essential states, past of estimate etter b x max arg : explanation ely lik Most Pt 1: )t 1: e|t 1: x( channel noisy a with ding deco recognition, eech sp 6 1–5 Sections 15, Chapter

L g-I suopos'gI dodeyo go quapuadepu!)queasuoo aeds pue aw!L ()d=]yM (1+J)CHVMHO=1+] (Fx)d(x 1+X)dx(1+Xta)do (1ax)d(a4x+X)dx☒(+X1+约)do=(+a|+X)d :X ino Bulwwns Kq uonpipald 'uonewnsa uonplpaud"' (F1+x)d(1+X|+)do (6|I+X)d(6T+X|+)do= (1++X)d=(1++x)d ((x)d'+)f=(1++x)d u叫Iμo31euoI1euIs331 ens aArs.In0a,Ie3s1 ap :wly uIO!H
Filtering rithm: algo estimation state e recursiv a devise Aim: )) t 1: e|t X( P, +1 t e( f =) +1 t 1: e| +1 t X( P ) +1 t e,t 1: e| +1 t X( P =) +1 t 1: e| +1 t X( P )t 1: e| +1 t X( P)t 1: e, +1 t X| +1 t e( Pα = )t 1: e| +1 t X( P) +1 t X| +1 t e( Pα = X out summing yb Prediction . estimation + rediction p I.e., t: )t 1: e|t x( P)t 1: e,t x| +1 t X( Pt x Σ) +1 t X| +1 t e( Pα =) +1 t 1: e| +1 t X( P )t 1: e|t x( P)t x| +1 t X( Pt x Σ) +1 t X| +1 t e( Pα = )t 1: e|t X( P=t 1: f where ) +1 t e,t 1: f( ard w or F = +1 t 1: f )t of endent (indep t constan space and Time 7 1–5 Sections 15, Chapter
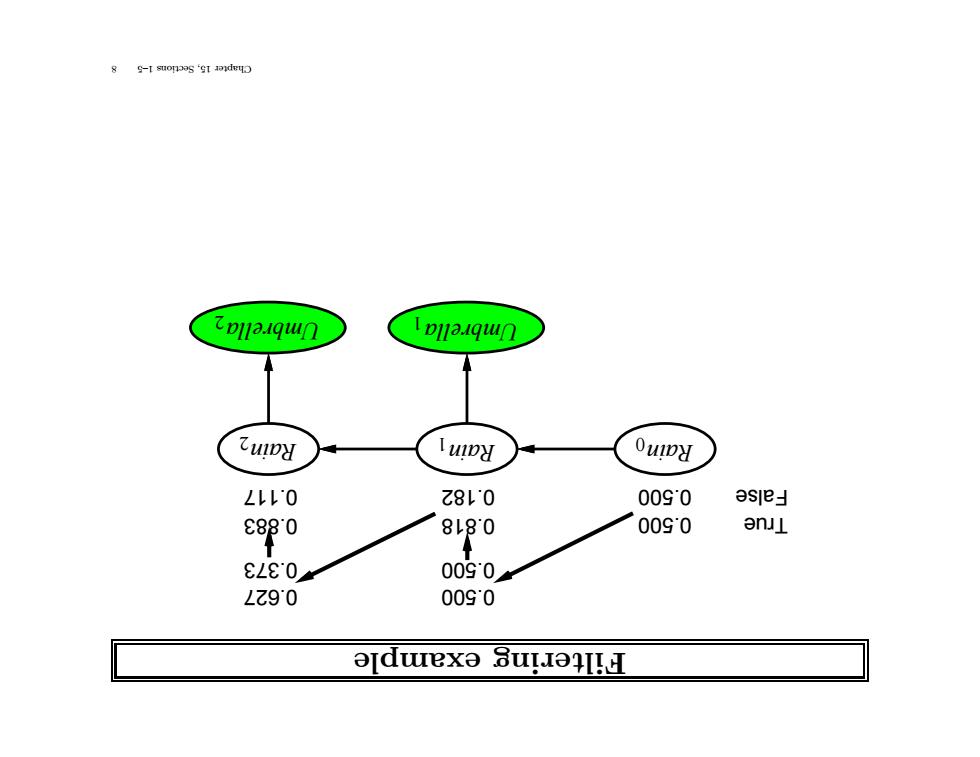
8 g-I suonoos'gt ℃p11a.qun Ipllaiqun 乙u1DH luiy Ouiy LLLO Z8L0 0090 3se」 e88^0 8L8^0 0090 anJL 、 ELE0 0090。 LZ9^0 0090 odwexo 3uI1!H
example Filtering Rain1 Umbrella1 Rain2 Umbrella2 Rain0 0.818 0.182 0.627 0.373 0.883 0.117 True False 0.500 0.500 0.500 0.500 8 1–5 Sections 15, Chapter

6S-1so19S‘gT4dw3 (X+x)d(+x+)d(1+xI+)d= (X+x)d(+x+d= (Xx)d(1+xX)d=(X+)d uolsuna spiemypeq e Kq paindwoo agessew puemypeg EI+YqYIJO (X|1+)d(x)do (X+)d(x)do= (T+治wolX)d=(oYX)d :1:1+Ya:Ta oul FTa aouapina pIA! Suryloows
othing Smo 1 X 0 X t E k E 1 E t X k X :t +1: k e, k 1: e into t 1: e evidence Divide )t +1: k e, k 1: e| k X( P =)t 1: e| k X( P )k 1: e, k X|t +1: k e( P)k 1: e| k X( Pα = )k X|t +1: k e( P)k 1: e| k X( Pα = t +1: k bk 1: f α = recursion: rds a backw a yb computed message rd a Backw )k X| +1 k x( P) +1 k x, k X|t +1: k e( P+1 k x Σ =)k X|t +1: k e( P )k X| +1 k x( P) +1 k x|t +1: k e( P +1 k x Σ = )k X| +1 k x( P) +1 k x|t +2: k e( P) +1 k x| +1 k e( P +1 k x Σ = 9 1–5 Sections 15, Chapter
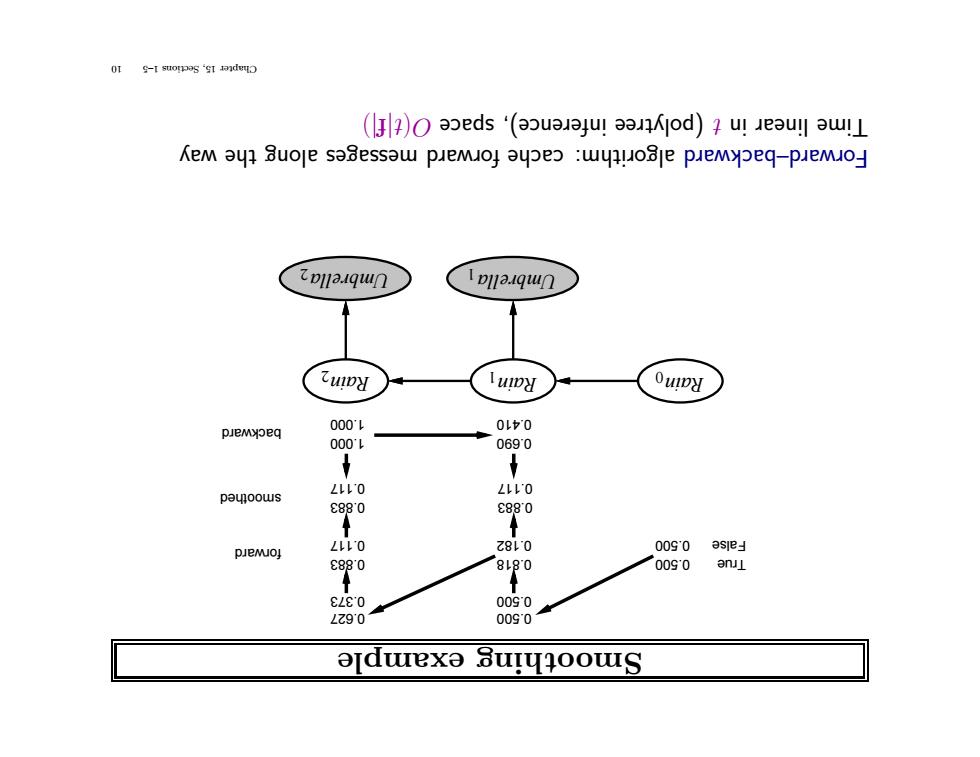
(J2)Oeds‘(uu!3Kod)?u!eu川uL Kem ay1 Buoje saBessaw puemuoy aypeo wynloe piemypeq-puemoy 乙112.qun Ipllaqun 乙u1DH luny OuIy piemyoeq 0001 0L0 0001 0690 payoows ∠↓0 LLL'O e880 8880 pieMoy LLL'O Z8L0 0090 asjey c880 8L80 0090 ELE0 0090 LZ901 0090 alduexa
example othing Smo Rain1 Umbrella1 Rain2 Umbrella2 Rain0 True False 0.818 0.182 0.627 0.373 0.883 0.117 0.500 0.500 0.500 0.500 1.000 1.000 0.690 0.410 0.883 0.117 forward backward smoothed 0.883 0.117 ya w the along messages rd a rw fo cache rithm: algo rd a rd–backw a rwoF )|f|t( O space inference), olytree (p t in r linea Time 10 1–5 Sections 15, Chapter