
【g-1som9 S'gI dD G-I SNOILOS GI HLdVHO STH(OW ALITavaoud IvHOdNL
models obability pr Temporal 1–5 Sections 15, Chapter 1 1–5 Sections 15, Chapter

8uuB4y1pIμed◇ syJomiau uelsaKeg olweu (uonuaw jauq e)saily uewjey sjapow noyeW uapp!H◇ 8uI叫1 oous 'uo14pIp3d‘8uμg3uul◇ K4uIeμ3 un pue3wuIL◇ ourino
Outline y uncertaint and Time ♦ othing smo rediction, p filtering, Inference: ♦ dels mo ov rk Ma Hidden ♦ mention) rief b (a filters Kalman ♦ rks ow net esian y Ba Dynamic ♦ filtering rticle aP ♦ 2 1–5 Sections 15, Chapter

g-I suopos'gI dodeyo X1-X+XX=X :uoneoN wajqod uo spuadap azis dans :owrg azaosIp sounsse siyL ayDTpooHyasmd 6nSpoolgpa.msvaw 7 awn ie sajqeuen aouapina ajqenjasqo jo 1as 14squaquoDyoDwois 6nSpoolg 2 awn ie sajqeuen alens ajqenasqoun jo 1as =X dans awn ypea joy sajqeuen aouapIna pue anens Adoo eap!oiseg sisougelp applyan sA quawageuew seneqel 1!1paud pue yoen on paau am :segueyp plom ay_ Aqureglooun pue ow!L
yt uncertain and Time it redict p and track to need e w changes; rld ow The diagnosis vehicle vs management etes Diab step time each r fo riables va evidence and state y cop idea: Basic t time at riables va state unobservable of set =t X ar ug oodS l B e.g., t ontents tomachC S, t etc. , t time at riables va evidence observable of set =t E ar ug oodS l edB easur M e.g., t ate seR ul P, t aten oodE F, t roblem p on ends dep size step ; time discrete assumes This a X Notation: a X =b: X, . . . , +1 a X, 1 −b X, b 3 1–5 Sections 15, Chapter
pg-I suonoos'gt e oy paxy (XHd lapow josuas pue (T-XX)d pow uonsue :ssaood Keuones (d=()d :uondwnsse Aoyew Josuas +4 -1 lepJo-puooas 乙+1 1 JapJo-1sJl (I-X-)d=(1-10xX)d:ssaood noyeW Japo-puoas (1-XX)d=(IXx)d :ssaood AoxeW Jpo-1s! I-F0X Jo 1asqns papunoq uo spuadap 'X :uondunsse Aoyew isquaed :selqeuen asay woyj au saKeg e ansuo) surey5 AoyIe) sossoood AoyIeI
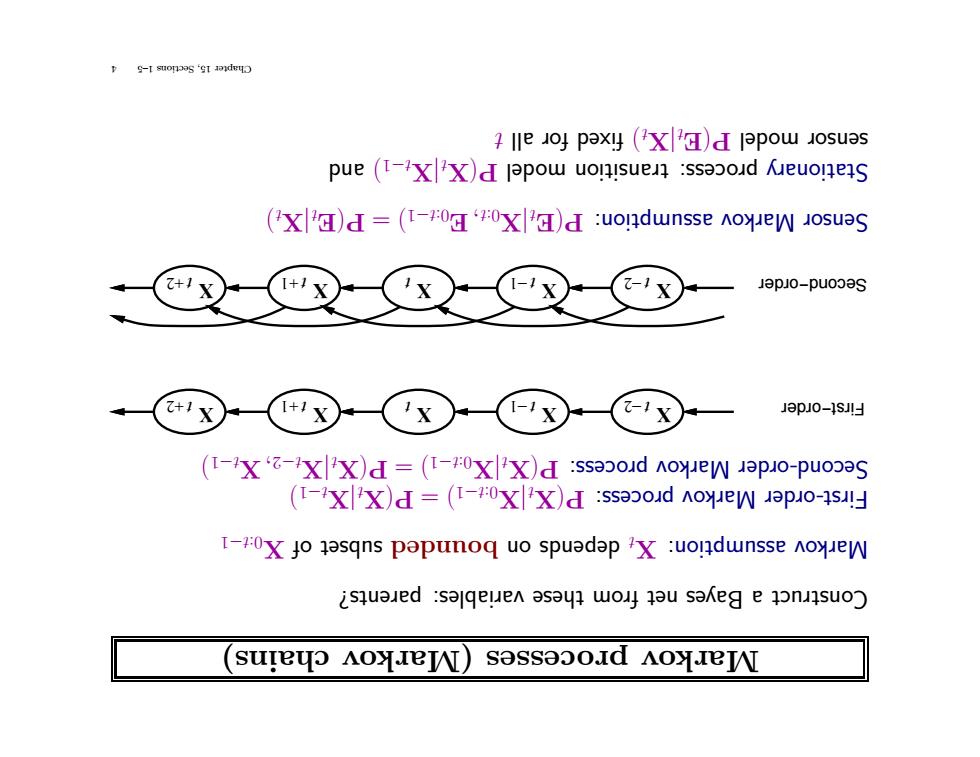
hains) c vo (Mark cesses pro vo Mark rents? pa riables: va these from net es y Ba a Construct 1 −t 0: X of subset ounded b on ends dep t X: assumption ov rk Ma )1 −t X|t X( P =)1 −t 0: X|t X( P: cess ro p ov rk Ma rder First-o )1 −t X, 2 −t X|t X( P =)1 −t 0: X|t X( P: cess ro p ov rk Ma rder Second-o +2 t X +1 t X t X −1 t X −2 t X +2 t X +1 t X t X −1 t X −2 t X First−order Second−order )t X|t E( P =)1 −t 0: E,t 0: X|t E( P: assumption ov rk Ma r Senso and )1 −t X|t X( P del mo transition cess: ro p ry Stationa t all r fo fixed )t X|t E( P del mo r senso 4 1–5 Sections 15, Chapter
g9-I suonos'gI todo f.ang yIM Ao pue uonsod quaw3ny uo14 ou noqo.13 dwex妇 lauinssa.ld "dua I ppe "3a 'anens quowsny 't ssaood Aoyuew Jo op.Io asea.IouI' s3X刈∂9Iss0d ipJom lea u!an Kpexe nou uondwnsse noyueW Japo-1s!y 1+1p1a1qu2 pllaiqwn 1-1pmaxqwn 0 (n)d +luind uind 1-luid L01 (Wd 1-4 odwexH
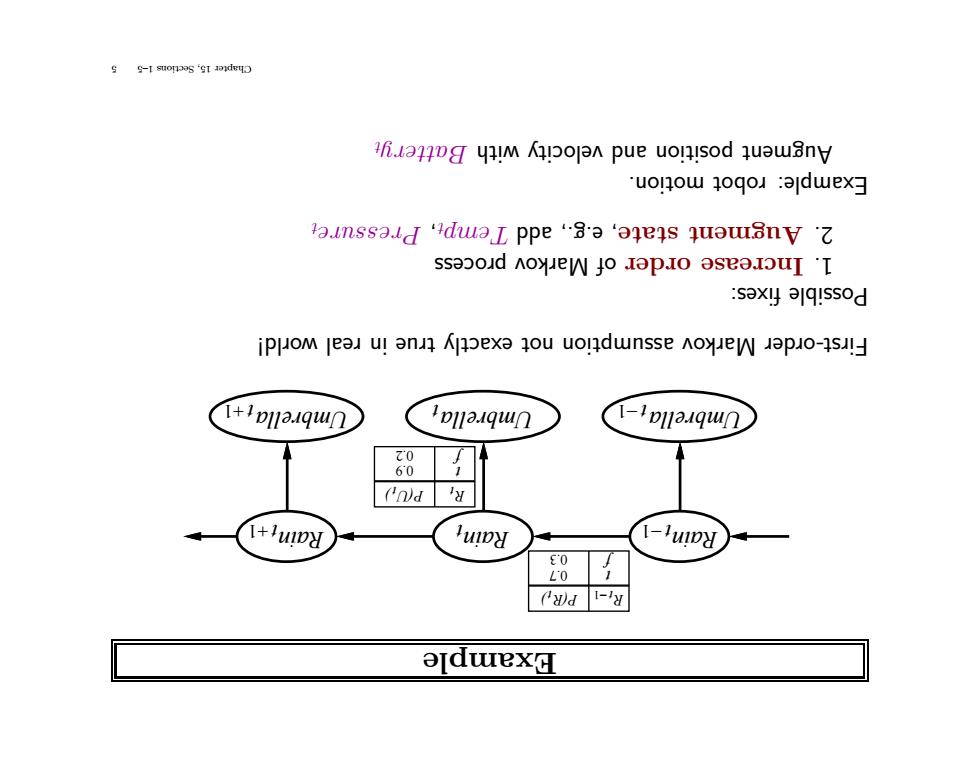
Example t Rain t Umbrella Rain −1 t Umbrella −1 t Rain +1 t Umbrella +1 t t P(R ) −1 t R 0.3 f 0.7 t t P(U ) t R 0.9 t 0.2 f rld! ow real in true exactly not assumption ov rk Ma rder First-o fixes: ossible P cess ro p ov rk Ma of order Increase 1. emp T add e.g., , state t Augmen 2. t e essur r P, t motion. ot rob Example: t y atter B with y cit velo and osition p Augment 5 1–5 Sections 15, Chapter