
-I SNOILOHS O HLdVHO ONINHVHT IVOILSILVLS
learning tistical a St 1–3 Sections 20, Chapter 1 1–3 Sections 20, Chapter

乙8-1suo139S0元ndgD uoIssaa Jeaull enep anajdwoo yiIm Sulujeal Jaewejed TW 8 ulujea]au s3Ke8◇ Bulueal pooy!jay!l wnwixew pue uowa]sod e wnwixeW Sulue3 ueis3Ke9◇ aurlinO
Outline rning lea esian y Ba ♦ rning lea do eliho lik maximum and ri osterio p a Maximum ♦ rning lea net es y Ba ♦ data complete with rning lea rameter pa ML – regression r linea – 2 1–3 Sections 20, Chapter

8 g-I suopos '07 isisayiodKy ssan3-isaq auo yoid o1 paau oN (p4)d(4x)d=(p4)d(4'Px)d=(px)d :sasaynodKy ayl Jano aBeJane pany3iam-pooy!lay!l e asn suolo!pald pooy!lay!l ay palleo s!(yp)d ayM (4d(yp)do=(p4d Aulqeqoud Jouansod e sey sisaynodKy ypea 'ej os enep ayn uanl) Np·p=p enep Buiuien alqeuen wopue jo awooino ay1 san!3p uoneasqo yif (Hd oudy sanjen 'alqeuen sisaynodKy ay s!H apeds sisayiodKy ay1 Jano uonnquas!p Auqeqod e yo 3uepdn ueisaKeg se ulue Ma!A Suruleol uelsoxeg IInH
learning esian y Ba ull F distribution y robabilit p a of dating up esian y Ba as rning lea View space othesis hyp the over ) H( Pr rio p,. . . , 2 h, 1 h values riable, va othesis hyp the is H j D riable va random of outcome the gives j d observation th j Nd, . . . , 1 d =d data training y: robabilit p r osterio p a has othesis hyp each r, fa so data the Given )i h( P)i h| d( Pα =) d|i h( P do eliho lik the called is )i h| d( P where otheses: hyp the over average eighted d-w o eliho lik a use Predictions ) d|i h( P)i h| X( Pi Σ =) d|i h( P)i h, d| X( Pi Σ =) d| X( P othesis! hyp est-guess b one pick to need No 3 1–3 Sections 20, Chapter

g-I suonos '07 1deD iaq Kpueo axau ay IlM nonel ieyM i!s!eq jo puly ieyM ●●●●●●●●●●:8 eq awos woy umeup s3pue3u3 sqo am uay 8 salpue au!l %00I e %0I salpue aw!l %SL+salpue Kuayp %9 :y ae %0 salpue au!l %09+salpue Kuay %0g :y e %0 sa!pue aw!l %9+salpue Kuayp %SL:y e %0 salpue Kuay %00I :t e%0I :salpueo jo sBeq jo spuiy anly ae auay]asoddns odwexH
Example candies: of bags of kinds five re a there ose Supp candies cherry 100% : 1 h re a 10% candies lime 25% + candies cherry 75% : 2 h re a 20% candies lime 50% + candies cherry 50% : 3 h re a 40% candies lime 75% + candies cherry 25% : 4 h re a 20% candies lime 100% : 5 h re a 10% bag: some from wn dra candies observe e w Then e? b candy next the will flavour What it? is bag of kind What 4 1–3 Sections 20, Chapter
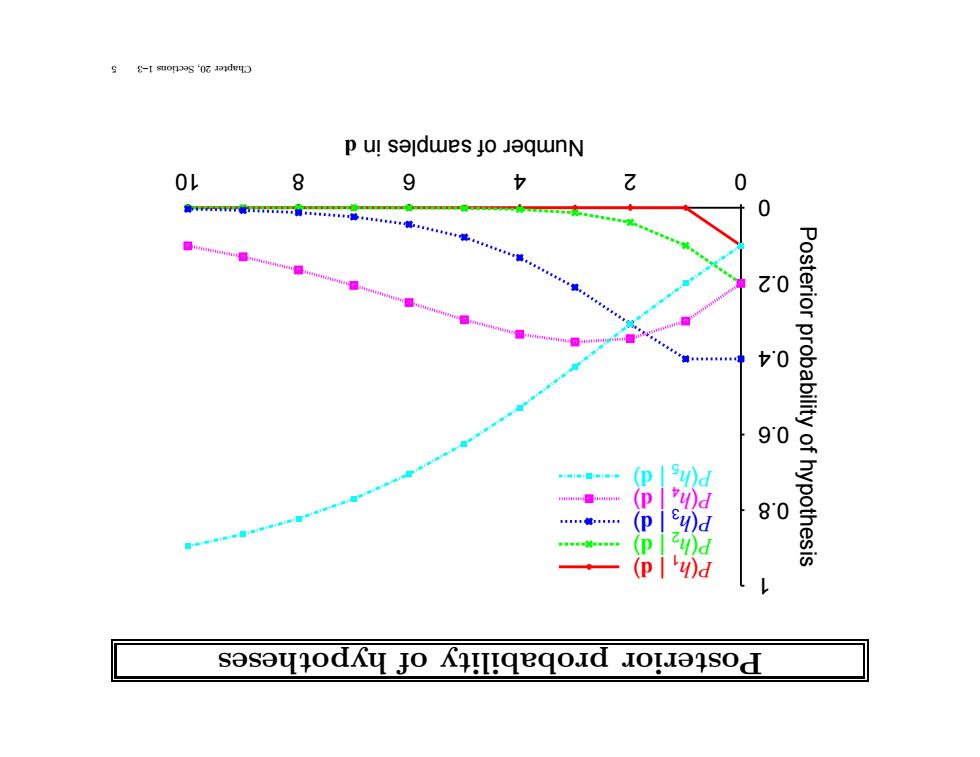
s g-I suonos '0 p u!sajdwes jo jaqwnN OL 8 9 b 乙 0 0 ◆ t0 9^0 (P su)d (P vy)d Posterior probability of hypothesis 制 (P a 80 (P d (P )d sasouodAy Jo Kil!qeqoid IoLonsod
otheses yp h of y probabilit osterior P 0 0.2 0.4 0.6 0.8 1 10 8 6 4 2 0 Posterior probability of hypothesis d Number of samples in ) d | 1 h( P ) d | 2 h( P ) d | 3 h( P ) d | 4 h( P ) d | 5 h( P 5 1–3 Sections 20, Chapter