
9I HLVHO SNOISIOHI IVNOILVY
decisions tional Ra 16 Chapter 1 16 Chapter
uolewJoju!o3neΛ◇ Sμ04 u uoIs1P30◇ s31l4n31nque41nW◇ KuoW◇ s3l4n◇ s3u3 gad jeuor4eH◇ ourino
Outline references p Rational ♦ Utilities ♦ Money ♦ utilities Multiattribute ♦ rks ow net Decision ♦ rmation info of alue V ♦ 2 16 Chapter
9I adeyD Ko1 pauajaud 1ou g axv pue uaamnaq aouaajj!pu! &~/ 9o1 pauejaud a</ :uonenoN d-I [a‘(d-)yd=Tu4o7 d s3zIμduIeμeoun yaIM suoI1ens3!‘s3μo1pue(3a‘/)s3zud8 uowe s3 sooy1ue8euV seoualojeld
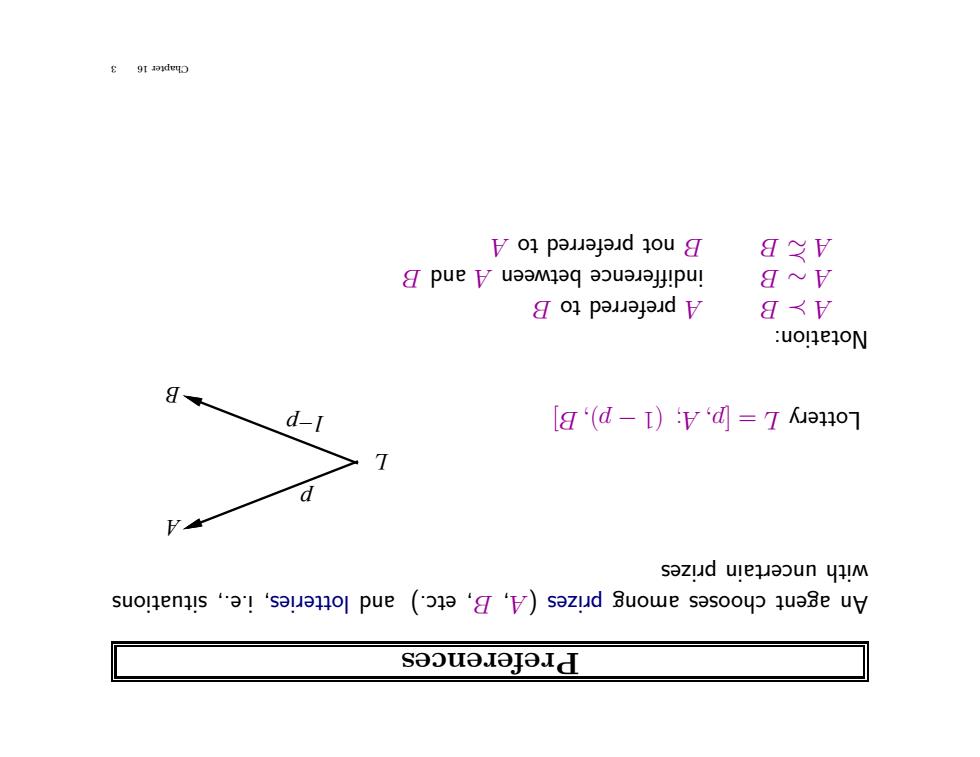
Preferences situations i.e., , lotteries and etc.) , B, A( rizes p among oses cho agent An rizes p uncertain with ] B,) p − (1 ; A p, [ = L Lottery L p 1−p A B Notation: B to referred p A B A B and A een wet b indifference B ∼ A A A to referred p not B B ∼ 3 16 Chapter

(ab-IVbX[ad-IVd台b<d←a<y KluonouoW [Od-[ad~[Od-LVd←8~/ K4μqen4!4sqnS g~o'd-1vd dE =0383V Kinunuo) (O</)=(0<a)V(a<) KsueL (a~V)∧(H<a)A(a<V) K!qepO :squlensuo) Kn panpadxa jo uoneziwixew se a]qequosap JoIneyaq ←s3u3Bed1euo4e squlensuoo Kaqo isnw quage jeuolel e jo seoualajald :eapl sooualajaId leuo!ey
preferences Rational constraints. ey ob must agent rational a of references p Idea: ⇒ references p Rational y utilit ected exp of maximization as describable r ehavio b Constraints: y Orderabilit ) B ∼ A( ∨) A B( ∨) B A( y ransitivit T ) C A( ⇒) C B( ∧) B A( y Continuit B ∼] C p, −1 ; A p, [ p ∃ ⇒ C B A y Substitutabilit ] C p, −1; B p, [ ∼] C p, −1 ; A p, [ ⇒ B ∼ A y Monotonicit ] B p, −1 ; A p, [ ⇔q ≥p( ⇒ B A ]) B, q −1 ; A, q[ ∼ 4 16 Chapter
9I adeyo 13 01 qua I (Kes)Ked pinom 01 sey oym quae ue uay Jl 133 01 u I(Kes)Ked pinom g sey oym quage ue uay'g 1301 u I (Kes)Ked pinom sey oym quaRe ue uay 'gl Kauow si e Keme nI8o1 paonpul aq ueo saouajajad anllsuenul yhlm quage ue :a]dwexe joy Keuonejl quapIna-jJas on speal squlensuoo ayn gunejo! 'pquoo sooualojold leuorey
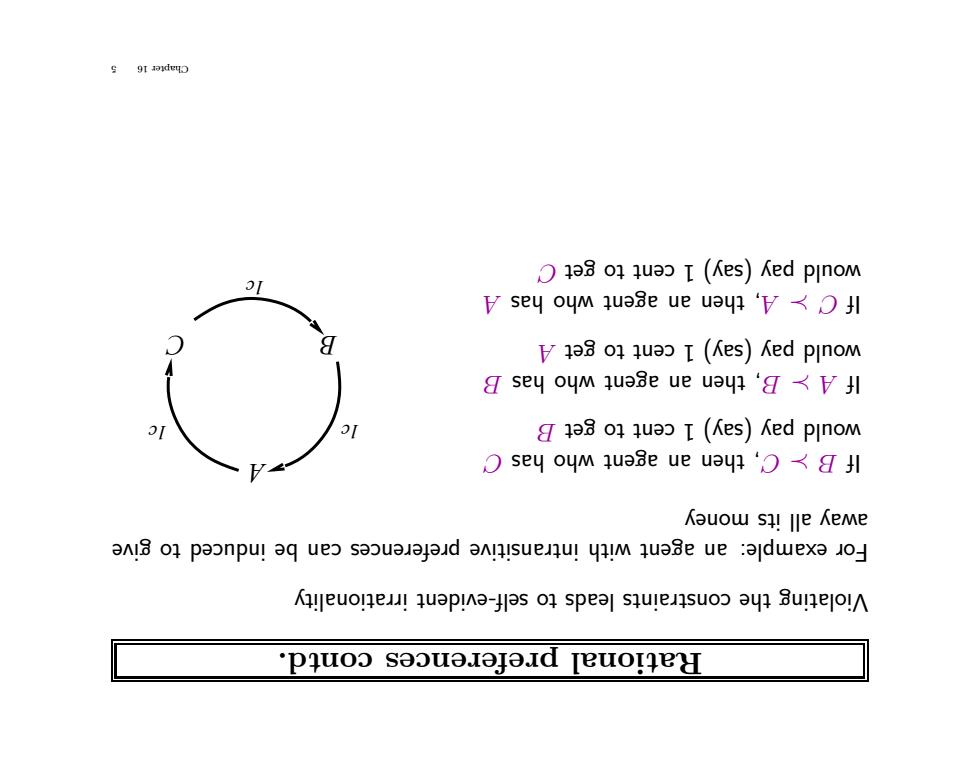
td. con preferences Rational y irrationalit self-evident to leads constraints the Violating give to induced eb can references p intransitive with agent an example: r oF money its all ya wa C has who agent an then , C B If B get to cent 1 y) (sa y pa ould w B has who agent an then , B A If A get to cent 1 y) (sa y pa ould w A has who agent an then , A C If C get to cent 1 y) (sa y pa ould w A C B 1c 1c 1c 5 16 Chapter