SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 吸=F(c四-Ax2dt o=E[(x(t)-E[x(t)])2] 经=经+呢 说明: ①候=E[x2(t]=0x2(t)dt 4R() ②ψ好:描述信号的强度 σ:描述信号的波动分量 ?:描述信号的静态分量 ③信号的均值和方差越大,信号的强度越高 机越与电气工程学院
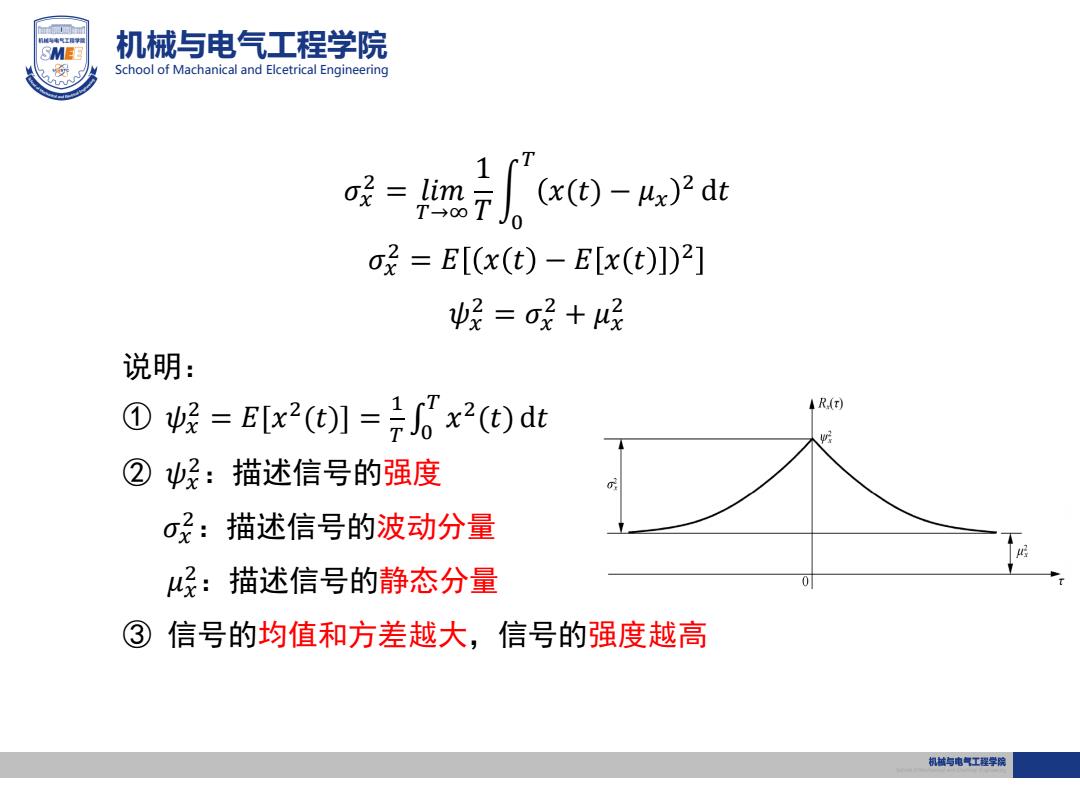
机械与电气工程学院 School of Machanical and Elcetrical Engineering 𝜎𝑥 2 = 𝑙𝑖𝑚 𝑇→∞ 1 𝑇 0 𝑇 𝑥(𝑡) − 𝜇𝑥 2 d𝑡 𝜎𝑥 2 = 𝐸 𝑥 𝑡 − 𝐸 𝑥 𝑡 2 𝜓𝑥 2 = 𝜎𝑥 2 + 𝜇𝑥 2 说明: ① 𝜓𝑥 2 = 𝐸[𝑥 2 (𝑡)] = 1 𝑇 0 𝑇 𝑥 2 (𝑡) d𝑡 ② 𝜓𝑥 2:描述信号的强度 𝜎𝑥 2:描述信号的波动分量 𝜇𝑥 2:描述信号的静态分量 ③ 信号的均值和方差越大,信号的强度越高

机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、信号的幅值域特征值 对于随机信号,其幅值的变化难以用具体的函数来描述,因 为它本身就毫无规律可言。然而对于大多数的平稳随机信号,可 以用统计的方法来描述信号取值的可能性,这就要用到概率统计 的数学方法。 (一)概率密度函数 设P[x≤x(t)≤x+△x]为信号x(t)的幅值在[x,x+△x]范围内取值 的概率,定义概率密度函数为 P[x≤x(t)≤X+△x] p(x)= lim △X→0 △X 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 二、信号的幅值域特征值 (一)概率密度函数 设𝑃[𝑥 ⩽ 𝑥(𝑡) ⩽ 𝑥 + Δ𝑥]为信号𝑥(𝑡)的幅值在 𝑥, 𝑥 + Δ𝑥 范围内取值 的概率,定义概率密度函数为 𝑝(𝑥) = 𝑙𝑖𝑚 Δ𝑥→0 𝑃[𝑥 ⩽ 𝑥(𝑡) ⩽ 𝑥 + Δ𝑥] Δ𝑥 对于随机信号,其幅值的变化难以用具体的函数来描述,因 为它本身就毫无规律可言。然而对于大多数的平稳随机信号,可 以用统计的方法来描述信号取值的可能性,这就要用到概率统计 的数学方法
SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 说明: 1.通过建立时域特征值映射到幅值特征值: 4x=∫txp(x)dt、经=∫tox2p(x)dt。 2.p(x)预测信号的趋势 (二)概率密度函数的实用公式 lim 季 4x(t) p(x)= △X→0△X (Tx是取值时间之和) 机越与电气工程学院
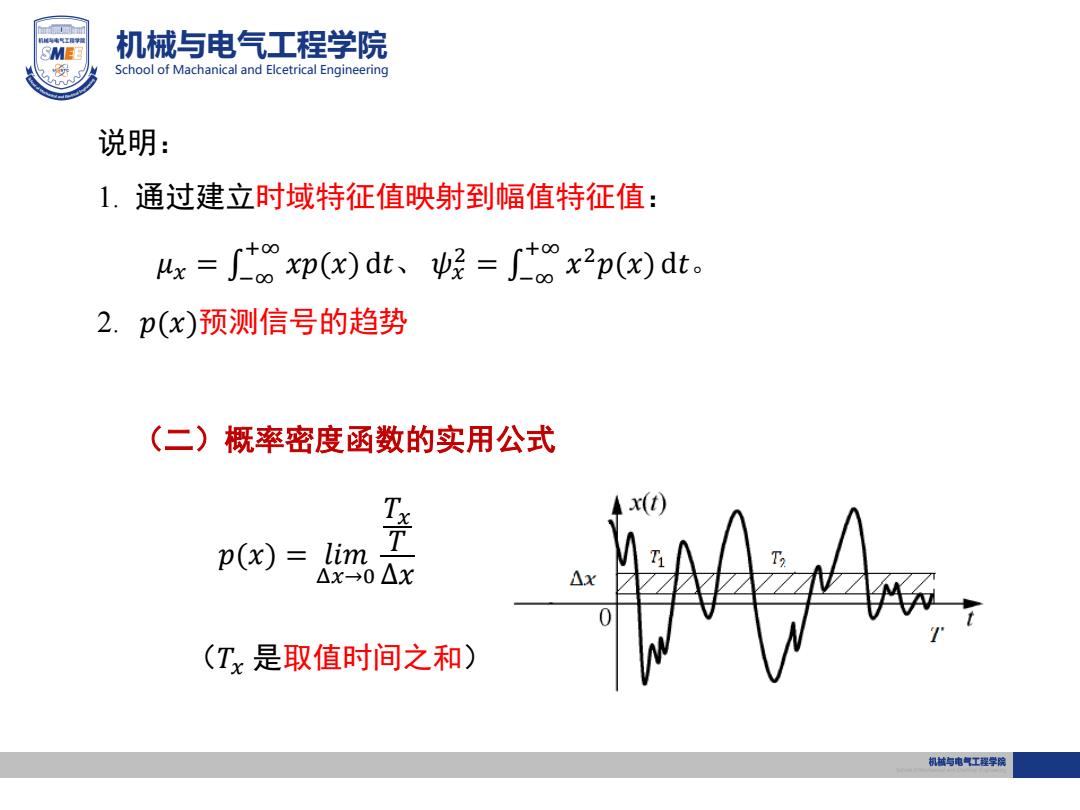
机械与电气工程学院 School of Machanical and Elcetrical Engineering 说明: 1. 通过建立时域特征值映射到幅值特征值: 𝜇𝑥 = −∞ +∞ 𝑥𝑝(𝑥) d𝑡、 𝜓𝑥 2 = −∞ +∞ 𝑥 2𝑝(𝑥) d𝑡。 2. 𝑝(𝑥)预测信号的趋势 (二)概率密度函数的实用公式 𝑝(𝑥) = 𝑙𝑖𝑚 Δ𝑥→0 𝑇𝑥 𝑇 Δ𝑥 (𝑇𝑥 是取值时间之和)

机械与电气工程学院 School of Machanical and Elcetrical Engineering 三、信号的相关域特征值 (一)自相关函数 表征信号与其本身在时移τ后的关联程度,它描述了信号自身 变化的平稳性,即变化缓慢还是剧烈。 1.连续信号x(t)的自相关函数,其中τ为观测间隔: ()t 对于平稳随机信号,上式变为: Rx()=lim子∫x(t)x(t+t)p(x)dt T00 机越与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 三、信号的相关域特征值 (一)自相关函数 表征信号与其本身在时移𝜏后的关联程度,它描述了信号自身 变化的平稳性,即变化缓慢还是剧烈。 1. 连续信号𝑥(𝑡)的自相关函数,其中𝜏为观测间隔: 𝑅𝑥(𝜏) = 𝑙𝑖𝑚 𝑇→∞ 1 𝑇 0 𝑇 𝑥(𝑡) 𝑥(𝑡 + 𝜏)d𝑡 对于平稳随机信号,上式变为: 𝑅𝑥(𝜏) = 𝑙𝑖𝑚 𝑇→∞ 1 𝑇 0 𝑇 𝑥(𝑡) 𝑥(𝑡 + 𝜏)𝑝(𝑥)d𝑡

SMEE 机械与电气工程学院 School of Machanical and Elcetrical Engineering 2.连续信号x(t)采样所得的离散信号的自相关函数,其中△t为采样时间, r是时间滞后量级,r=0,1,2..m: n-r Rr·△t)= 1 n-rL Xk Xk+r k=1 机城与电气工程学院
机械与电气工程学院 School of Machanical and Elcetrical Engineering 2. 连续信号𝑥(𝑡)采样所得的离散信号的自相关函数,其中Δ𝑡为采样时间, 𝑟是时间滞后量级,𝑟 = 0,1,2 … m : 𝑅𝑥(𝑟 ⋅ Δ𝑡) = 1 𝑛 − 𝑟 𝑘=1 𝑛−𝑟 𝑥𝑘 𝑥𝑘+𝑟