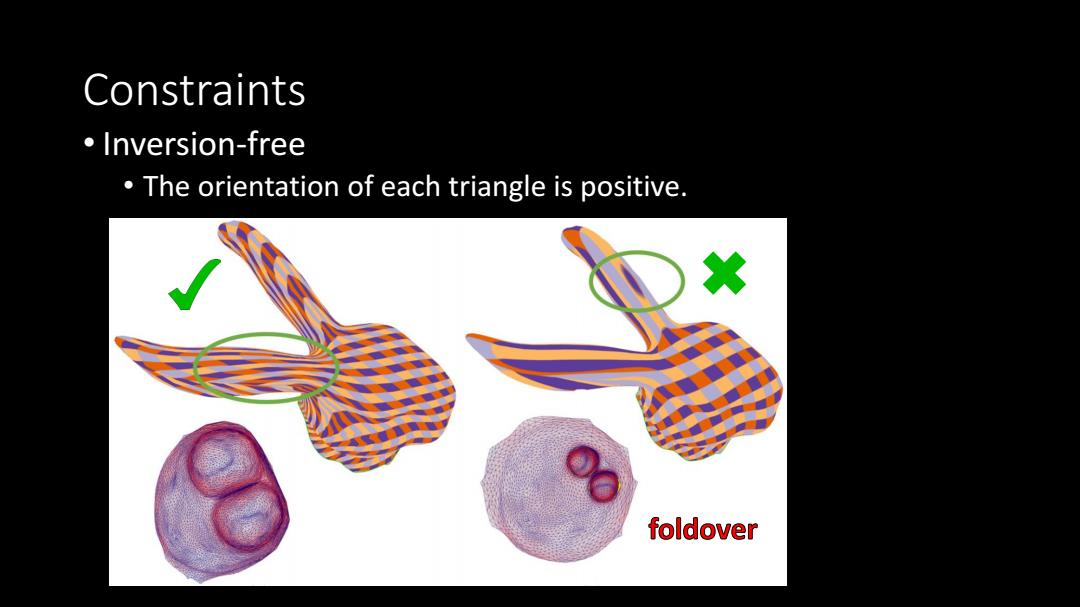
Constraints 。Inversion-free The orientation of each triangle is positive. 然 foldover
Constraints • Inversion-free • The orientation of each triangle is positive
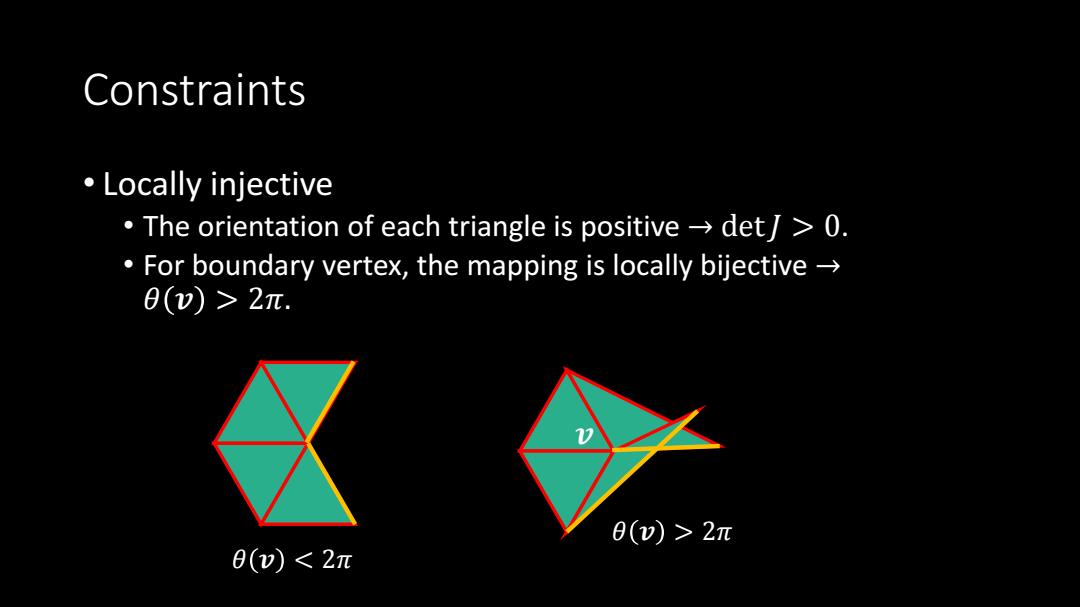
Constraints ·Locally injective The orientation of each triangle is positive det>0. For boundary vertex,the mapping is locally bijective-> 0()>2π. 0()>2π θ()<2π
Constraints • Locally injective • The orientation of each triangle is positive → det𝐽 > 0. • For boundary vertex, the mapping is locally bijective → 𝜃 𝒗 > 2𝜋. 𝜃 𝒗 < 2𝜋 𝜃 𝒗 > 2𝜋 𝒗
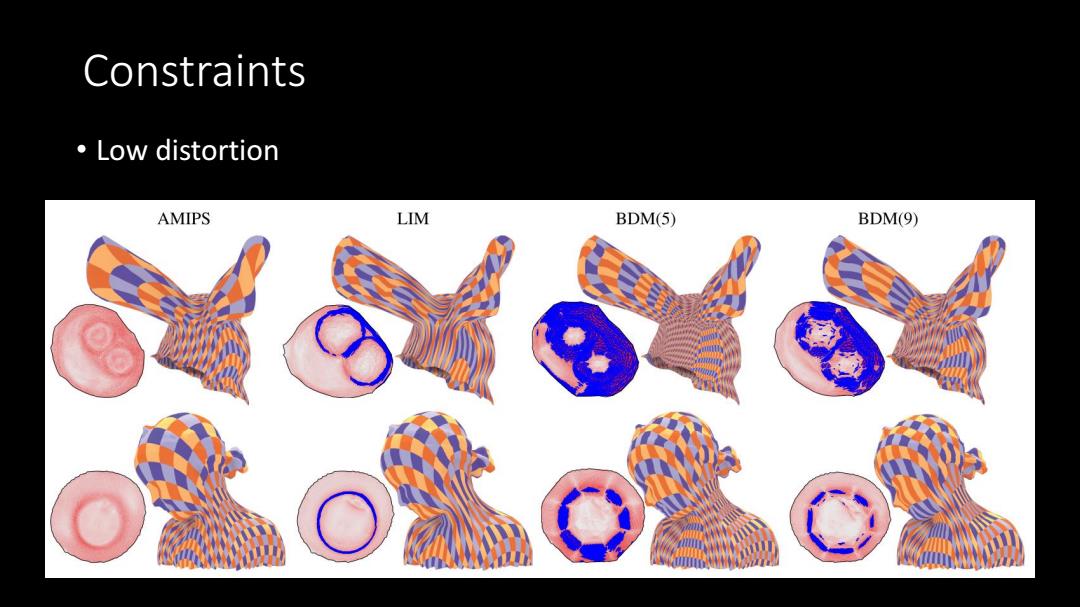
Constraints 。Low distortion AMIPS LIM BDM(5) BDM(9)
Constraints • Low distortion

Outline 。Definition Tutte's barycentric mapping Least squares conformal maps(LSCM,ASAP) Angle-Based Flattening (ABF) ·ABF+,LABF As-rigid-as-possible (ARAP) 。Simplex Assembly
Outline • Definition • Tutte’s barycentric mapping • Least squares conformal maps(LSCM, ASAP) • Angle-Based Flattening (ABF) • ABF++, LABF • As-rigid-as-possible (ARAP) • Simplex Assembly

Barycentric Mapping One of the most widely used methods. Given a triangulated surface homeomorphic to a disk,if the (u,v)coordinates at the boundary vertices lie on a convex polygon in order,and if the coordinates of the internal vertices are a convex combination of their neighbors,then the (u,v)coordinates form a valid parameterization (without self-intersections,bijective)
Barycentric Mapping • One of the most widely used methods. Given a triangulated surface homeomorphic to a disk, if the (𝑢, 𝑣) coordinates at the boundary vertices lie on a convex polygon in order, and if the coordinates of the internal vertices are a convex combination of their neighbors, then the (𝑢, 𝑣) coordinates form a valid parameterization (without self-intersections, bijective)