电子科技大学：《电路分析基础 Electric Circuit Analysis》课程教学资源（授课教案）第十四章 动态电路的频域分析

根据电感电流的拉普拉斯变换，查拉普拉斯变换表 14一1，可以得到电感电流的零输入响应、零状态响应 和全响应为 零输入响应 i(t)=(-5e'+9e-31)ε(t)A 零状态响应 →"(t)）=(e-e-3)ε(t)A 全响应 8 →i(t)=(-4e-+8e-3)ε(t)A 此题的计算结果和例9一5用时域分析方法得到的结果 相同

根据电感电流的拉普拉斯变换，查拉普拉斯变换表 14－1，可以得到电感电流的零输入响应、零状态响应 和全响应为 ( ) ( 4e 8e ) ( )A ( 3) 8 ( 1) 4 ( ) (e e ) ( )A ( 3) 1 ( 1) 1 ( ) ( 5e 9e ) ( )A ( 3) 9 ( 1) 5 3 L 3 L 3 L i t t s s i t t s s i t t s s t t " t t ' t t                                                   全响应 零状态响应 零输入响应 此题的计算结果和例9－5用时域分析方法得到的结果 相同

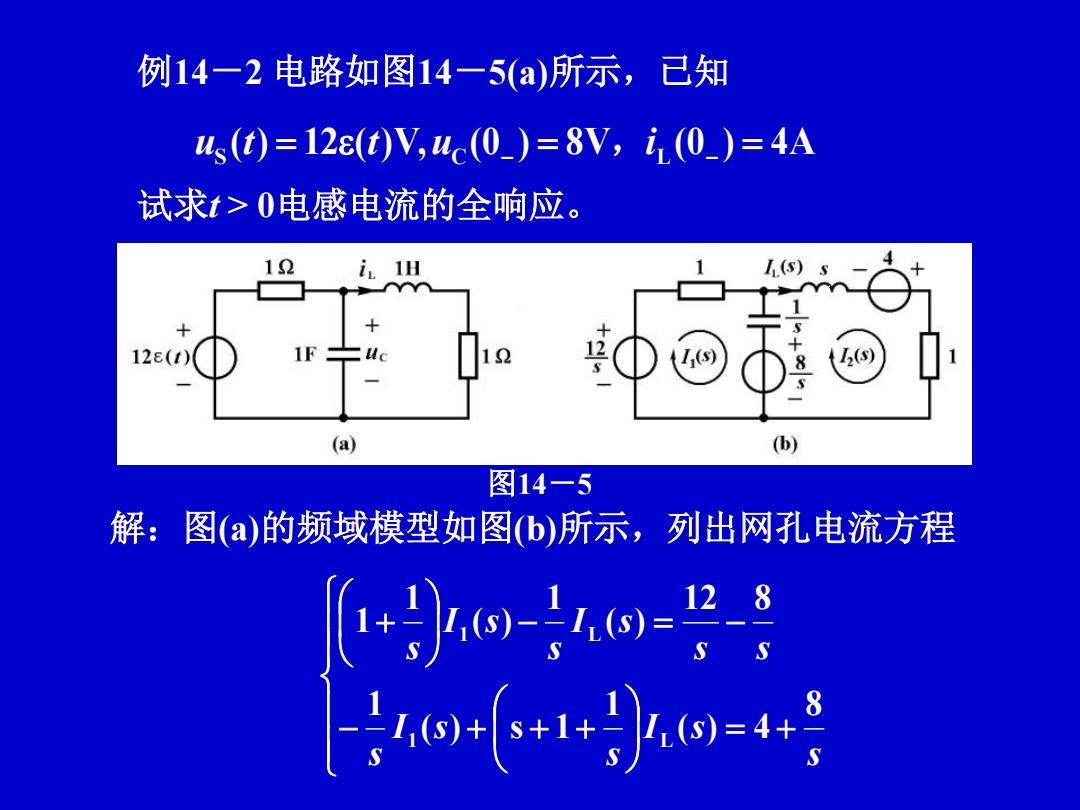
例14一2电路如图14一5(a)所示，已知 ws(t)=12ε(t)V,uc(0)=8V,i0_)=4A 试求t>0电感电流的全响应。 I(S) 12e( 1 8 (a) (b) 图14一5 解：图(a的频域模型如图b)所示，列出网孔电流方程 +o-w= 128 +1.网=

例14－2 电路如图14－5(a)所示，已知 试求t > 0电感电流的全响应。 uS (t)  12(t)V, uC (0 )  8V，i L (0 )  4A 解：图(a)的频域模型如图(b)所示，列出网孔电流方程 图14－5                              s I s s I s s s s I s s I s s 8 ( ) 4 1 ( ) s 1 1 12 8 ( ) 1 ( ) 1 1 1 L 1 L

求解得到电感电流的拉普拉斯变换后，再用部分分式 展开为 4(s2+3s+3)6. -2s I(S)= (s2+2s+2) Ss2+2s+2 6 -2S (s+1-j(s+1+) 6-1-j,-1+j s+1-is+1+j 查拉普拉斯变换表可以得到电感电流为 i,(t)=[6+2W2e'cost-135A

求解得到电感电流的拉普拉斯变换后，再用部分分式 展开为 1 j 1 j 1 j 6 1 j ( 1 j)( 1 j) 6 2 2 2 6 2 ( 2 2) 4( 3 3) ( ) 2 2 2 L                             s s s s s s s s s s s s s s s s I s 查拉普拉斯变换表可以得到电感电流为 L ( ) [6 2 2e cos( 135 )]A      i t t t

§14一3线性时不变电路的性质 频域形式的表格方程 表格方程由KCL、KVL和元件VCR方程组成。现在以 图14一6电路加以说明。 i2 RI ② ③ is us(t) R2 O 图14一6

§14－3 线性时不变电路的性质 一、频域形式的表格方程 表格方程由KCL、KVL和元件VCR方程组成。现在以 图14－6电路加以说明。 图14－6

1.用矩阵形式列出个结点的KCL方程 支路12345 L(s) 0 0 结点② 0 :9888 简写为 A(S)=0 其中 4 1 0 称为关联矩阵，它表示支路与结点的关联关系，其元素为

1．用矩阵形式列出个结点的KCL方程 简写为 AI(s)＝0 其中 称为关联矩阵，它表示支路与结点的关联关系，其元素为           0 0 0 1 1 0 1 1 1 0 1 1 0 0 0 － A＝ － －                                         0 0 0 ( ) ( ) ( ) ( ) ( ) 0 0 0 1 1 0 1 1 1 0 1 1 0 0 0 1 2 3 4 5 5 4 3 2 1 I s I s I s I s I s ③ ② ① 结 点 支 路