
敏感性分析图、表 敏感性分析表 因素变化率 30% -20% -10% 0 10% 20% 30% 产量 基准值 售价 基准值 固定成本 基准值 投资额 基准值 建设期 基准值 NPV 投资K 敏感性分析: 单位变动成本 可以对直线斜率绝对值的大小 进行排序,直线斜率绝对值越 大,说明该因素的敏感性越高, 产品售价P 即该因素给项目带来的风险就 变化率 越大
敏感性分析表 因素/变化率 -30% -20% -10% 0 10% 20% 30% 产量 基准值 售价 基准值 固定成本 基准值 投资额 基准值 建设期 基准值 敏感性分析: 可以对直线斜率绝对值的大小 进行排序,直线斜率绝对值越 大,说明该因素的敏感性越高, 即该因素给项目带来的风险就 越大。 NPV 变化率 单位变动成本 产品售价P 投资K 敏感性分析图、表

敏感性分析类型 1、单因素敏感性分析 特点:一次只变动一个因素 例题: 单位:元 项目 投资 寿命 残值 年收入 年支出 折现率 因素 10000 5 2000 5000 2200 8% 基本方案: NPV(8%)=-10000+(5000-2200PVIF4%s) +2000PIF4%s) =2541
1、单因素敏感性分析 ➢ 特点:一次只变动一个因素 单位:元 因素 10000 5 2000 5000 2200 8% 项目 投资 寿命 残值 年收入 年支出 折现率 ( ) ( )( ) ( ) 2541 2000 8% 10000 5000 2200 8% ,5 8% ,5 = + = − + − PVIFA NPV PVIFA 基本方案: 例题: 敏感性分析类型
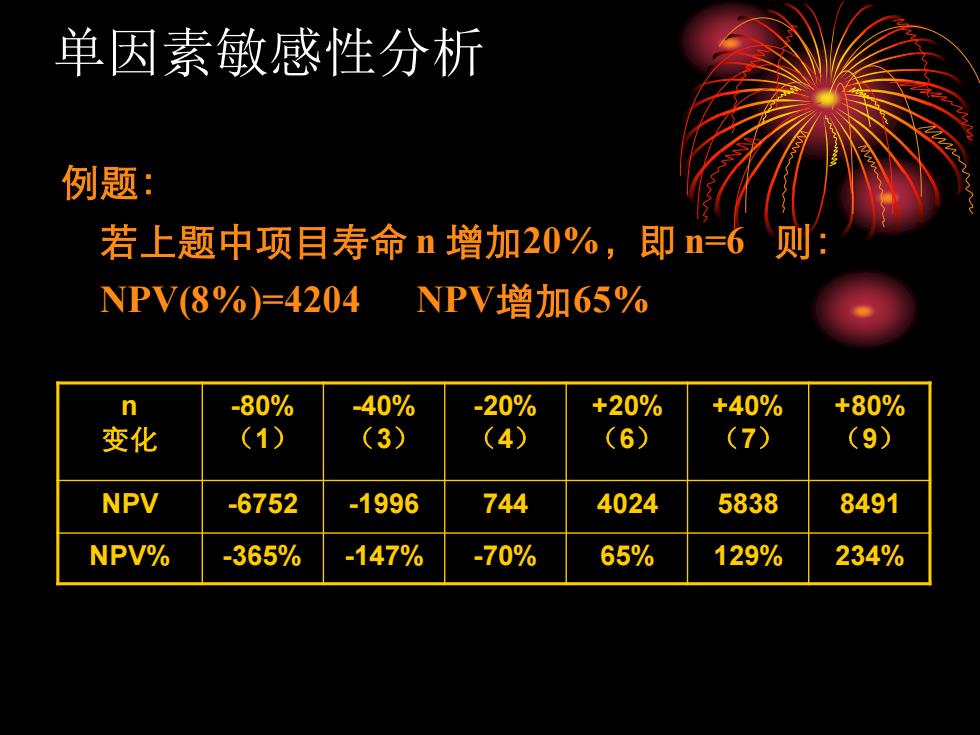
单因素敏感性分析 例题: 若上题中项目寿命n增加20%,即n=6则: NPV(8%)=4204 NPV增加65% n -80% -40% -20% +20% +40% +80% 变化 (1) (3) (4) (6) (7) (9) NPV -6752 -1996 744 4024 5838 8491 NPV% -365% -147% -70% 65% 129% 234%
例题: 若上题中项目寿命 n 增加20%,即 n=6 则: NPV(8%)=4204 NPV增加65% n 变化 -80% (1) -40% (3) -20% (4) +20% (6) +40% (7) +80% (9) NPV -6752 -1996 744 4024 5838 8491 NPV% -365% -147% -70% 65% 129% 234% 单因素敏感性分析

多因素敏感性分析 2、多因素敏感性分析(1) >特点:同时变动两个或两个以上因素 交互作用 例题: 投资— 变化幅度x,收入—变化幅度y NPV=-100001+x+50000+Jy)-2200(PMFA%s) +2000(PVIFA%5) =-10000x+19964y+2540 当NPV≥0,有y≥0.5x-0.127
2、多因素敏感性分析(1) ➢特点:同时变动两个或两个以上因素——交互作用 例题: 投资——变化幅度x,收入——变化幅度y ( ) ( ) ( ) ( ) 0 0.5 0.127 10000 19964 2540 2000 10000 1 5000 1 2200 8% ,5 8% ,5 − = − + + + = − + + + − NPV , y x x y PVIFA NPV x y PVIFA 当 有 多因素敏感性分析

多因素敏感性分析 2、多因素敏感性分析(2) >特点:同时变动三个因素 例题: 投资 变化幅度x,收入一变化幅度y,寿命为n NPV=-10000(1+x)+[5000(1+y)-2200]PVIFAS%?n) +2000(PVTFA) 当=2时,NPV≥0→y≥0.369+1.122x 当n=4时,NPV≥0=→y≥-0.045+0.604x 当=6时,NPV≥0→y≥-0.128+0.443x
2、多因素敏感性分析(2) ➢特点:同时变动三个因素 例题: 投资——变化幅度x,收入——变化幅度y,寿命为n ( ) ( ) ( ) ( ) n 6 NPV 0 y 0.128 0.443x n 4 NPV 0 y 0.045 0.604 x n 2 NPV 0 y 0.369 1.122x 2000 PVIFA NPV 10000 1 x 5000 1 y 2200 PVIFA 8%,n 8%,n = − + = − + = + + = − + + + − 当 时 , 当 时 , 当 时 , 多因素敏感性分析