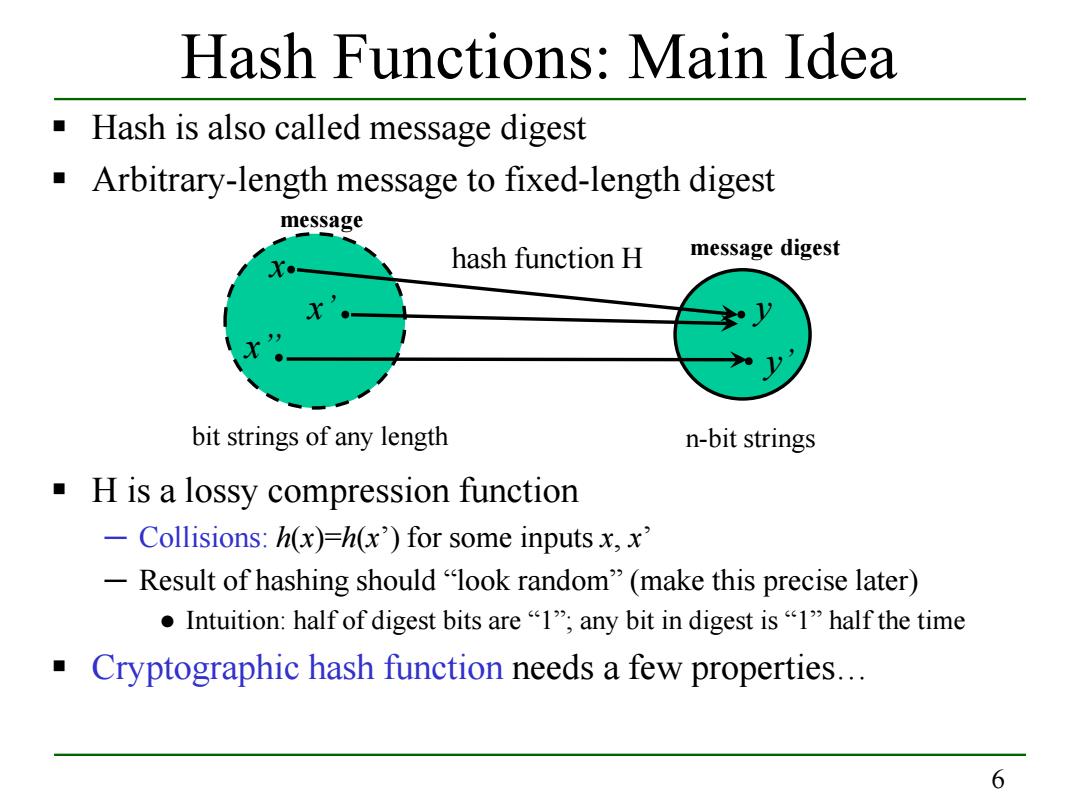
Hash Functions:Main Idea Hash is also called message digest Arbitrary-length message to fixed-length digest message hash function H message digest bit strings of any length n-bit strings H is a lossy compression function -Collisions:h(x)=h(x)for some inputs x,x' -Result of hashing should "look random"(make this precise later) ●Intuition:half of digest bits are“I',any bit in digest is“l”half the time Cryptographic hash function needs a few properties... 6
6 Hash Functions: Main Idea Hash is also called message digest Arbitrary-length message to fixed-length digest H is a lossy compression function ─ Collisions: h(x)=h(x’) for some inputs x, x’ ─ Result of hashing should “look random” (make this precise later) ● Intuition: half of digest bits are “1”; any bit in digest is “1” half the time Cryptographic hash function needs a few properties… bit strings of any length n-bit strings . . . . . x’ x’’ x y’ y hash function H message digest message

Hashes and Message Digest One-wayness:given h(x),hard to find x -Also called“pre-image resistance” Collision resistance:hard to find x,x'such that h(x)=h(x') -Also called "strong collision resistance" -Brute-force collision search is only O(2n/2),not 2n -Birthday Paradox -n needs to be at least 128 ■ Weak collision resistance:given x,hard to find x'such that h(x)=h(x') -Also called“second pre-image resistance” -Brute-force attack requires O(2m)time 7
7 Hashes and Message Digest One-wayness: given h(x), hard to find x ─ Also called “pre-image resistance” Collision resistance: hard to find x, x’ such that h(x)=h(x’) ─ Also called “strong collision resistance” ─ Brute-force collision search is only O(2n/2), not 2n ─ Birthday Paradox ─ n needs to be at least 128. Weak collision resistance: given x, hard to find x’ such that h(x)=h(x’) ─ Also called “second pre-image resistance” ─ Brute-force attack requires O(2n) time

One-Wayness Intuition:hash should be hard to invert -"Preimage resistance" -Leth(x)=y∈{0,l}for a random x' -Given y,it should be hard to find x such that h(x)= ▣How hard? -Brute-force:try every possible x,see if h(x)=y -SHA-1 (common hash function)has 160-bit output .Assuming 264 trials per second,can do 289 trials per year Will take 271 years to invert SHA-1 on a random image 8
8 One-Wayness Intuition: hash should be hard to invert ─ “Preimage resistance” ─ Let h(x’) = y ∈{0,1}n for a random x’ ─ Given y, it should be hard to find x such that h(x)=y How hard? ─ Brute-force: try every possible x, see if h(x)=y ─ SHA-1 (common hash function) has 160-bit output ● Assuming 264 trials per second, can do 289 trials per year ● Will take 271 years to invert SHA-1 on a random image

Collision Resistance (CR) Should be hard to find x,x'such that h(x)h(x) -Brute-force collision search is only O(22),not O(2") -For SHA-1,this means O(280)vs.O(2160) 9
9 Collision Resistance (CR) Should be hard to find x, x’ such that h(x)=h(x’) ─ Brute-force collision search is only O(2n/2), not O(2n) ─ For SHA-1, this means O(280) vs. O(2160)
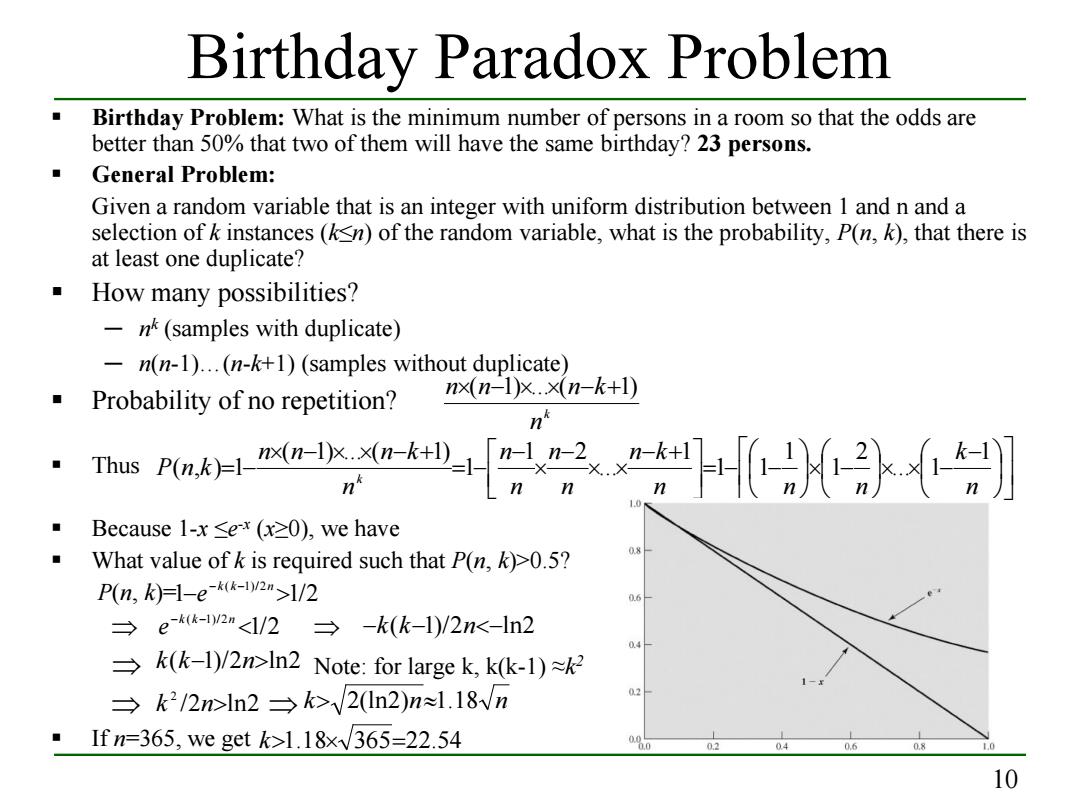
Birthday Paradox Problem Birthday Problem:What is the minimum number of persons in a room so that the odds are better than 50%that two of them will have the same birthday?23 persons. General Problem: Given a random variable that is an integer with uniform distribution between 1 and n and a selection of k instances(ksn)of the random variable,what is the probability,P(n,k),that there is at least one duplicate? How many possibilities? -nk(samples with duplicate) n(n-1)...(n-k+1)(samples without duplicate) Probability of no repetition? nx(n-1)x.×(n-k+l) n ·msw。三卧】 Because 1-x <ex (x20),we have What value of k is required such that P(n,k)>0.5? P(n,k)-1-e-k(k-by2n>1/2 →e-2m</2→-k(k-1)/2n<-n2 02 →k(k-l)/2>ln2Note:for large k,kk-l)≈k2 →k2/2>ln2→k>√2ln2)n≈l.18vn 0.2 Ifn=365,we get k>1.18x√365=22.54 02 04 0.6 0.8 10
10 Birthday Paradox Problem Birthday Problem: What is the minimum number of persons in a room so that the odds are better than 50% that two of them will have the same birthday? 23 persons. General Problem: Given a random variable that is an integer with uniform distribution between 1 and n and a selection of k instances (k≤n) of the random variable, what is the probability, P(n, k), that there is at least one duplicate? How many possibilities? ─ nk (samples with duplicate) ─ n(n-1)…(n-k+1) (samples without duplicate) Probability of no repetition? Thus Because 1-x ≤e-x (x≥0), we have What value of k is required such that P(n, k)>0.5? P(n, k)= ⇒ ⇒ ⇒ Note: for large k, k(k-1) ≈k2 ⇒ ⇒ If n=365, we get k n n×(n−1)×...×(n−k+1) − × × − × − = − − − + × × − × − = − × − × × − + = − n k n n n n k n n n n n n n n k P n k k 1 ... 1 2 1 1 1 1 1 ... 1 2 1 ( 1) ... ( 1) ( , ) 1 1 1/2 ( 1)/2 − > −k k− n e 1/2 ( 1)/2 < −k k− n e −k(k−1)/2n<−ln2 k(k−1)/2n>ln2 /2 ln2 2 k n> k> 2(ln2)n≈1.18 n k>1.18× 365=22.54