
Instance:n jobsj=1,...,n with processing times p;ER Solution:An assignment of n jobs to m identical machines that minimizes the makespan Cmax "minimum makespan on identical machines":PCmax Graham's“alβly'notation for scheduling a:machine environment ·l:a single machine; P:m identical machines; Q:m machines with different speed s;,the length of jobj on machine i is pi/s R:m unrelated machines,the length of jobj on machine i is pij ·β:job characteristics .release times;d:deadlines;pmtn:preemption; 。y:objective ·Cmax:makespan;∑,C:total completion time;Lmax:maximum lateness;
• α: machine environment • 1: a single machine; • P: m identical machines; • Q: m machines with different speed , the length of job j on machine i is ; • R: m unrelated machines, the length of job j on machine i is ; • β: job characteristics • : release times; : deadlines; pmtn: preemption; • γ: objective • : makespan; : total completion time; : maximum lateness; si pj /si pij rj dj Cmax ∑i Ci Lmax Graham’s “α|β| γ” notation for scheduling “minimum makespan on identical machines”: P| |Cmax Instance: jobs with processing times Solution: An assignment of jobs to identical machines that minimizes the makespan n j = 1,…, n pj ∈ ℝ+ n m Cmax

Instance:n jobsj=1,...,n with processing times p;ER Solution:An assignment of n jobs to m identica/machines that minimizes the makespan Cmax "minimum makespan on identical machines":PCmax Reducible from the partition problem: Instance:n numbers x1,..., Determine whethera partition of {1,2,...,n}into A and B such that】 ∑:=∑ iEA iEB One of Karp's 21 NPC problems
“minimum makespan on identical machines”: P| |Cmax Instance: jobs with processing times Solution: An assignment of jobs to identical machines that minimizes the makespan n j = 1,…, n pj ∈ ℝ+ n m Cmax Instance: numbers Determine whether a partition of into and such that . n x1, …, xn ∈ ℤ+ ∃ {1,2,…, n} A B ∑ i∈A xi = ∑ i∈B xi • One of Karp’s 21 NPC problems • Reducible from the partition problem:

Approximation Ratio Instance:n jobsj=1,...,n with processing times p; Solution:An assignment of n jobs to m identica/machines that minimizes the makespan Cmax An algorithm for a minimization problem has approximation ratio a if SOLI V instance I, ≤ OPTI SOL:solution returned by the algorithm on instance I OPT:optimal solution of instance I
Instance: jobs with processing times Solution: An assignment of jobs to identical machines that minimizes the makespan n j = 1,…, n pj ∈ ℝ+ n m Cmax An algorithm for a minimization problem has approximation ratio if instance , 𝒜 α ∀ I SOLI OPTI ≤ α • : solution returned by the algorithm on instance • : optimal solution of instance SOLI I OPTI I Approximation Ratio
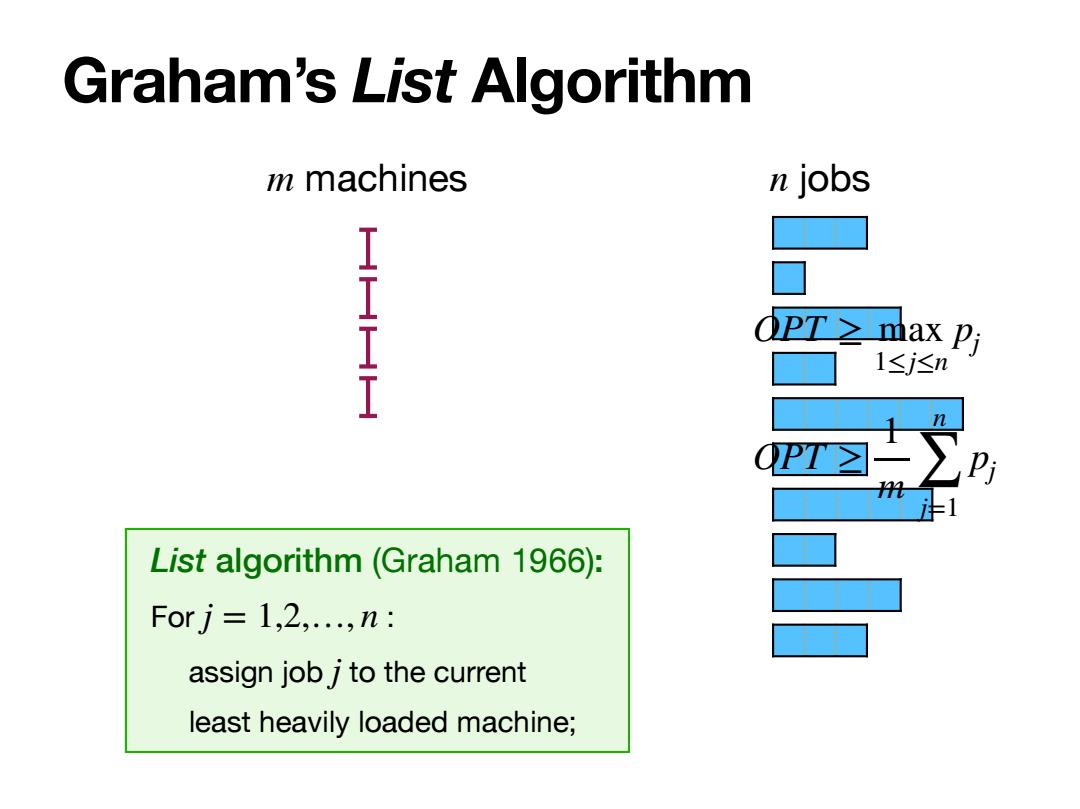
Graham's List Algorithm m machines n jobs dpT≥max Pi 1≤j≤n Pi 注1 List algorithm (Graham 1966): Forj=1,2,.,n: assign job j to the current least heavily loaded machine;
Graham’s List Algorithm m machines n jobs List algorithm (Graham 1966): For : assign job to the current least heavily loaded machine; j = 1,2,…, n j OPT ≥ max 1≤j≤n pj OPT ≥ 1 m n ∑ j=1 pj
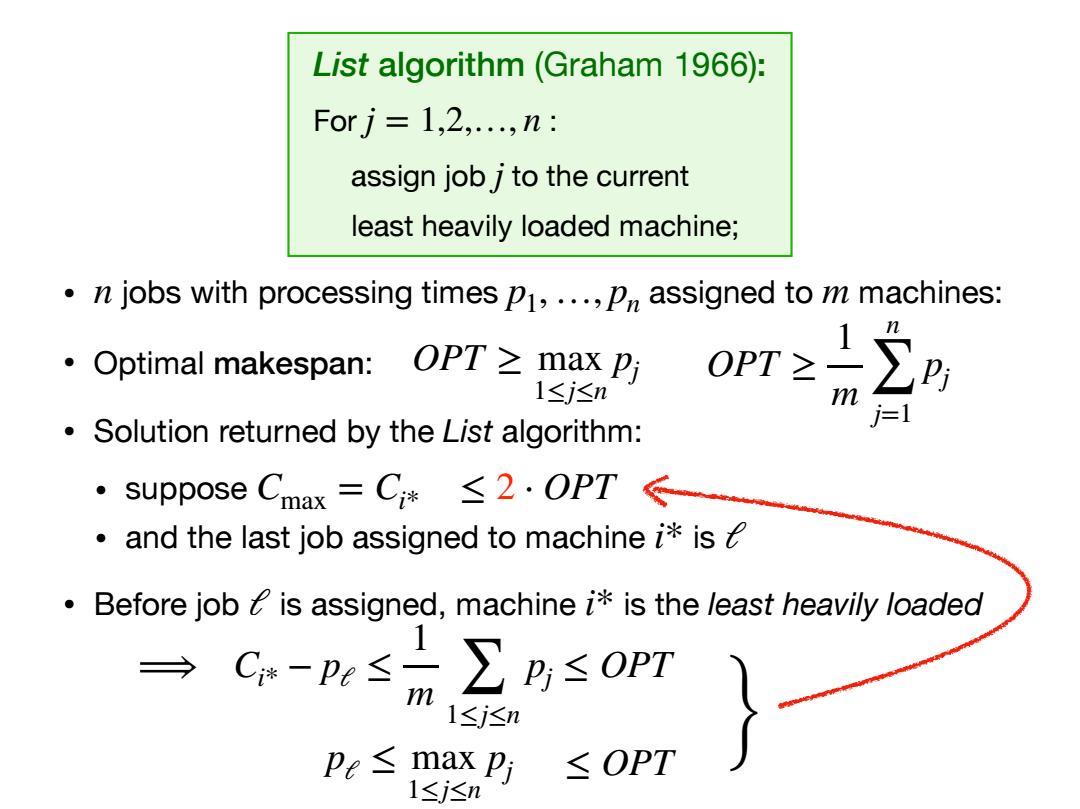
List algorithm (Graham 1966): Forj=1,2,.,n: assign job j to the current least heavily loaded machine; n jobs with processing times p1,...,Pn assigned to m machines: 。Optimal makespan:( OPT≥max Pi 1≤j≤n m j=1 Solution returned by the List algorithm: ·suppose Cmax=C*≤2.OPT← and the last job assigned to machine i is Before job is assigned,machine i is the least heavily loaded →C-P%≤∑m≤oPm m l≤j≤n pe≤max pi ≤OPT 1≤jsn
• jobs with processing times assigned to machines: • Optimal makespan: • Solution returned by the List algorithm: • suppose • and the last job assigned to machine is • Before job is assigned, machine is the least heavily loaded n p1,…, pn m Cmax = Ci* i* ℓ ℓ i* ⟹ Ci* − pℓ ≤ 1 m ∑ 1≤j≤n pj ≤ OPT List algorithm (Graham 1966): For : assign job to the current least heavily loaded machine; j = 1,2,…, n j OPT ≥ max 1≤j≤n pj OPT ≥ 1 m n ∑ j=1 pj pℓ ≤ max 1≤j≤n pj ≤ OPT } ≤ 2 ⋅ OPT