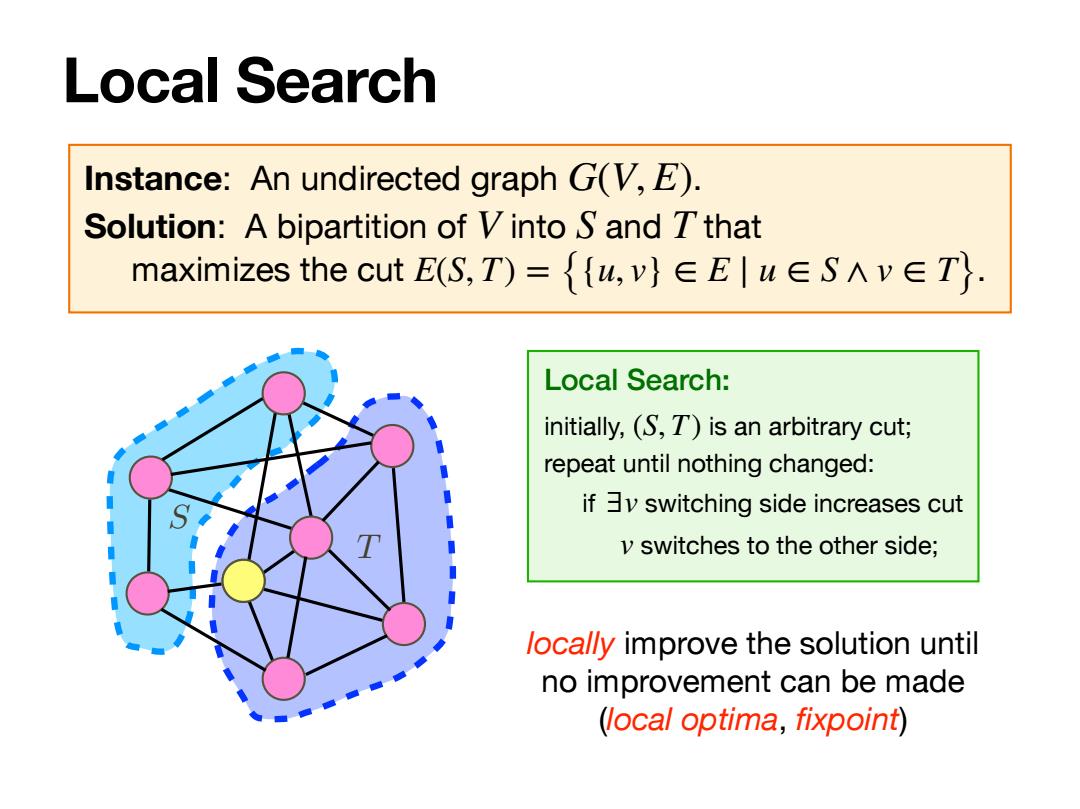
Local Search Instance:An undirected graph G(V,E). Solution:A bipartition of V into S and T that maximizes the cut E(S,T)={w,v}∈Eluw∈S∧v∈T}. Local Search: initially,(S,T)is an arbitrary cut; repeat until nothing changed: if v switching side increases cut v switches to the other side; locally improve the solution until no improvement can be made (local optima,fixpoint)
Local Search Instance: An undirected graph . Solution: A bipartition of into and that maximizes the cut . G(V, E) V S T E(S, T) = {{u, v} ∈ E ∣ u ∈ S ∧ v ∈ T} Local Search: initially, is an arbitrary cut; repeat until nothing changed: if switching side increases cut switches to the other side; (S, T) ∃v v locally improve the solution until no improvement can be made (local optima, fixpoint) T S

Local Search Local Search: initially,(S,T)is an arbitrary cut; repeat until nothing changed: ifv switching side increases cut v switches to the other side; in a local optima: v∈S:|E(y,S)川≤|E(y,T)川→21E(S,S)川≤|E(S,T)川 v∈T:|E(y,T)川≤IE(y,S)l→2|E(T,T)川≤IE(S,T)l E(S,S)+E(T,T)<E(S,T) OPT≤IE1=IE(S,S)川+IE(T,T)川+IE(S,T)I≤2|E(S,T)I →IE(S,T)I≥二OPT
Local Search Local Search: initially, is an arbitrary cut; repeat until nothing changed: if switching side increases cut switches to the other side; (S, T) ∃v v in a local optima: ∀v ∈ S : |E(v, S)| ≤ |E(v, T)| ⟹ 2|E(S, S)| ≤ |E(S, T)| ∀v ∈ T : |E(v, T)| ≤ |E(v, S)| ⟹ 2|E(T, T)| ≤ |E(S, T)| |E(S, S)| + |E(T, T)| ≤ |E(S, T)| OPT ≤ |E| = |E(S, S)| + |E(T, T)| + |E(S, T)| ⟹ |E(S, T)| ≥ 1 2 OPT ≤ 2|E(S, T)| T S

Scheduling
Scheduling

Scheduling processing m machines n jobs time pj 3 HH 9 1 4 HH 2 6 3 5 2 4 3
Scheduling m machines n jobs processing time pj 3 1 4 2 6 3 5 2 4 3
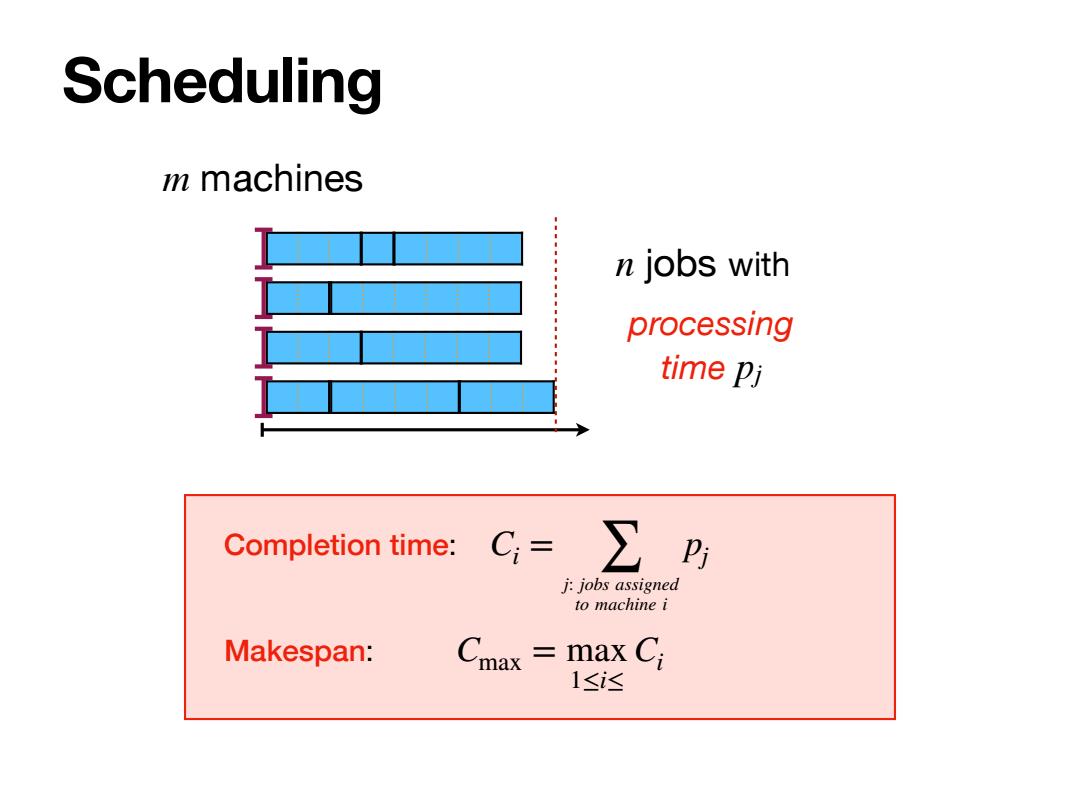
Scheduling m machines n jobs with processing time Pj Completion time: C=∑ j:jobs assigned to machine i Makespan: max ma <Ci 1≤i达
Scheduling n jobs m machines processing time pj with Completion time: Makespan: Ci = j: job ∑ s assigned to machine i pj Cmax = max 1≤i≤ Ci