
4.2.1 Asymptotic Spectral Distributions for Wigner matrix 0.31 0.25H 0.2 0.15 0.1 0.05 The semicircle law compared with the histogram of the average of 100 empirical density functions for a Wigner matrix of size n=100. 6
6 4.2.1 Asymptotic Spectral Distributions for Wigner matrix The semicircle law compared with the histogram of the average of 100 empirical density functions for a Wigner matrix of size n = 100

4.2.2 Asymptotic Spectral Distributions for Square Matrix Theorem 4.2.2.Let H be an N X N complex random matrix whose entries a are independent random variables with identical mean, variance 1/N and finite kth moments for k 4.Then,the asymptotic spectrum of H converges almost surely to the circular law [2],namely the uniform distribution over the unit disk on the complex plane {5∈C:g≤1 whose density is given by 无(传)-1 兀 [2]V.L.Girko,Circular Law [J],Theory Prob.Appl.,1984,29,647-709
7 4.2.2 Asymptotic Spectral Distributions for Square Matrix Theorem 4.2.2. Let H be an N × N complex random matrix whose entries are independent random variables with identical mean, variance 1/N and finite kth moments for k ≥ 4. Then, the asymptotic spectrum of H converges almost surely to the circular law [2], namely the uniform distribution over the unit disk on the complex plane whose density is given by 1 ( ) C f { : 1} [2] V. L.Girko, Circular Law [J],Theory Prob. Appl.,1984,29,647 - 709.

4.2.2 Asymptotic Spectral Distributions for Square Matrix 15 0.5 0 -0.5 -1 -1 -0.5 0 05 1 1.5 The full-circle law and the eigenvalues of a realization of a matrix of size n=500 8
8 4.2.2 Asymptotic Spectral Distributions for Square Matrix The full-circle law and the eigenvalues of a realization of a matrix of size n = 500

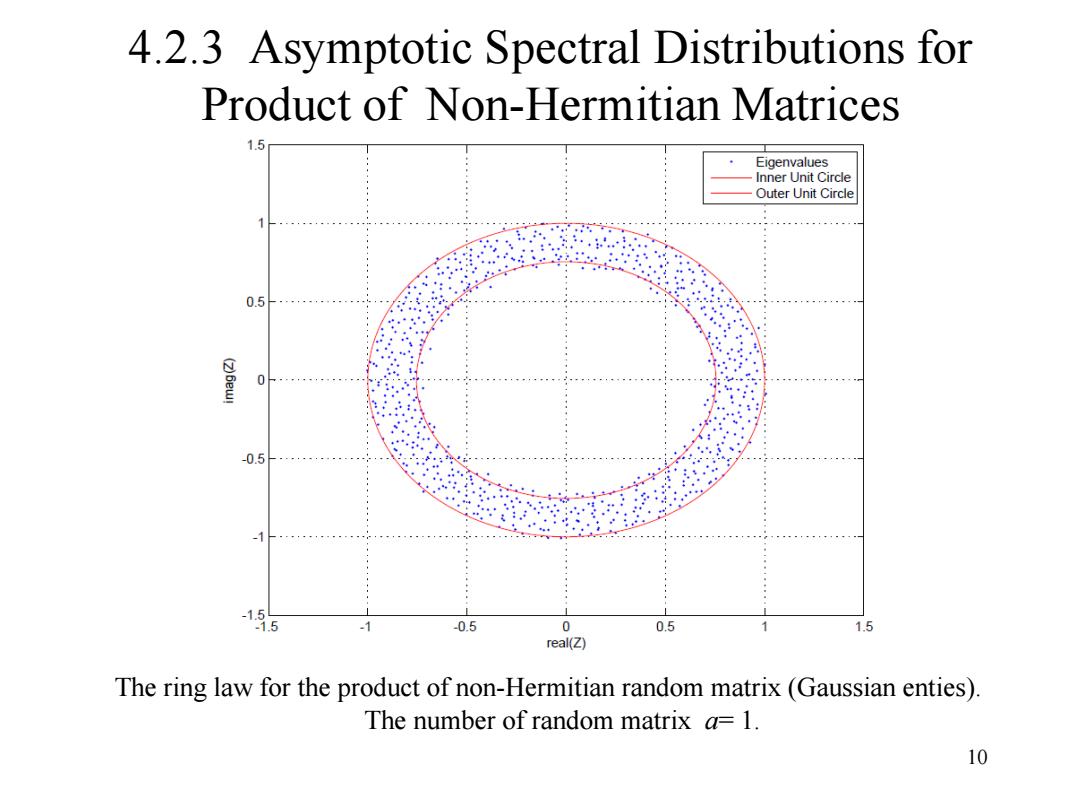
4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices Theorem 4.2.4.Consider an NXK (N>K)matrix H whose entries are independent zero-mean complex (or real)random variables with variance 1/N.As K,N-oo with KN->B.The product of non-Hermitian random matrices is defined as z=ΠX where X,is the singular value equivalent of Hie.x,=UH,where U is an unitary matrix.The empirical eigenvalue distribution of Z converge almost surely to the limit given by: o-- elsewhere This is called ring law. 9
9 4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices Theorem 4.2.4. Consider an N×K (N>K) matrix H whose entries are independent zero-mean complex (or real) random variables with variance 1/N. As K,N → ∞ with K/N→ β. The product of non-Hermitian random matrices is defined as where Xi is the singular value equivalent of Hi , .i.e. where U is an unitary matrix. The empirical eigenvalue distribution of Z converge almost surely to the limit given by: 1 a i i Z X 1 1 2/ 2 / 2 1 1 (z) 0 a i i a a z z f a elsewhere X † X U H H i i i This is called ring law
4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices 1.5 Eigenvalues Inner Unit Circle Outer Unit Circle 0.5 0 1. ,1 -0.5 -1 -1.5 1.5 -0.5 0 0.5 1.5 real(Z) The ring law for the product of non-Hermitian random matrix(Gaussian enties). The number of random matrix a=1. 10
10 4.2.3 Asymptotic Spectral Distributions for Product of Non-Hermitian Matrices The ring law for the product of non-Hermitian random matrix (Gaussian enties). The number of random matrix a= 1