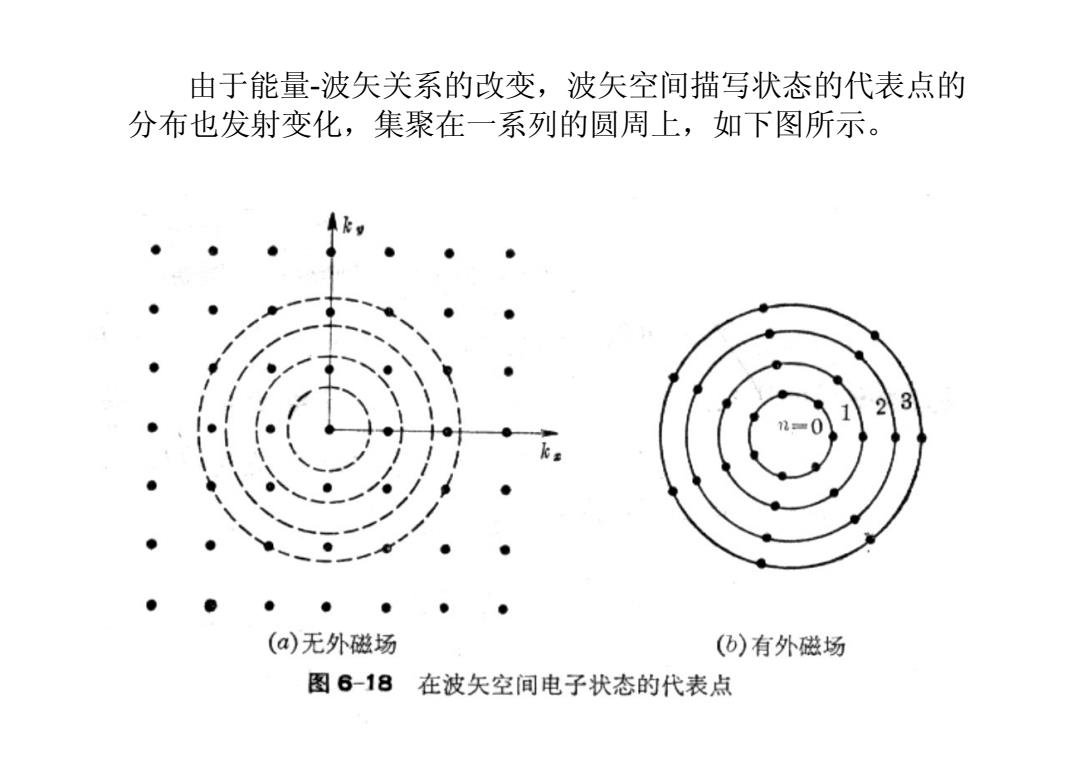
由于能量-波矢关系的改变,波矢空间描写状态的代表点的 分布也发射变化,集聚在一系列的圆周上,如下图所示。 23 (a)无外磁场 (b)有外磁场 图6-18在波矢空间电子状态的代表点
由于能量-波矢关系的改变,波矢空间描写状态的代表点的 分布也发射变化,集聚在一系列的圆周上,如下图所示
! 。05
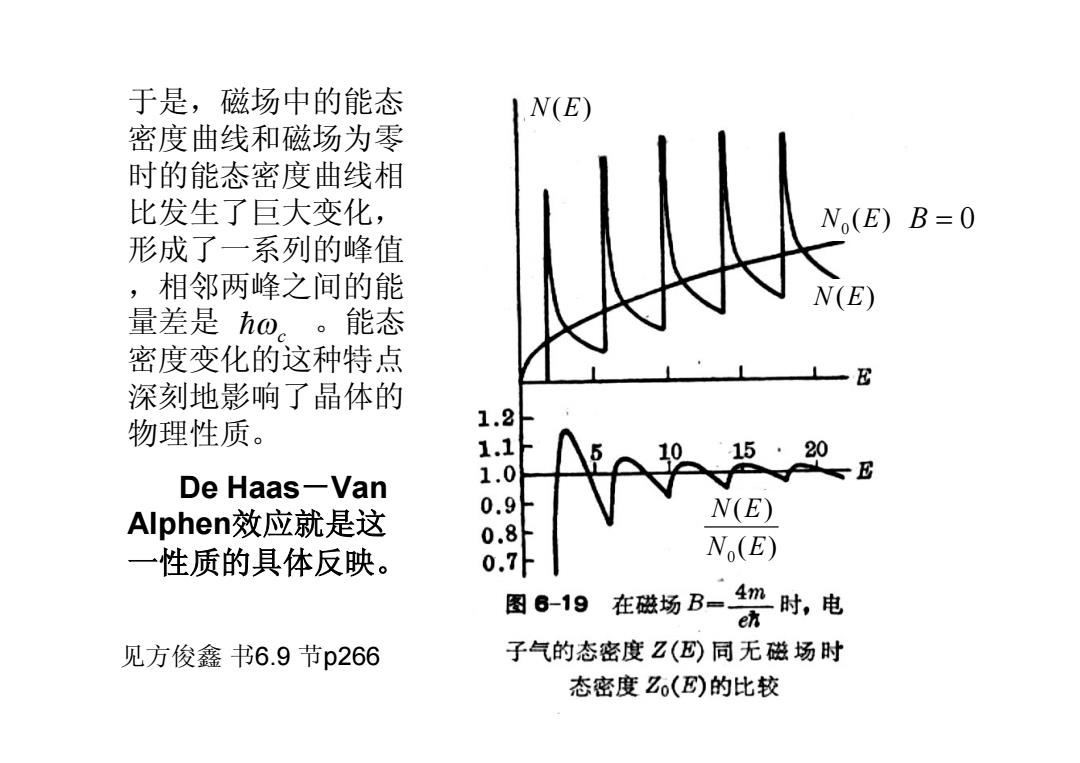
于是,磁场中的能态 N(E) 密度曲线和磁场为零 时的能态密度曲线相 比发生了巨大变化, N(E)B=0 形成了一系列的峰值 , 相邻两峰之间的能 N(E) 量差是ho。。能态 密度变化的这种特点 E 深刻地影响了晶体的 物理性质。 1.2 1.1 -E De Haas-Van 1.0 Alphen效应就是这 0.9 N(E) 0.8 一 性质的具体反映。 0.7 N(E) 图6-19 在磁场B一4n时,电 en 见方俊鑫书6.9节p266 子气的态密度Z()同无磁场时 态密度Zo()的比较
于是,磁场中的能 态 密度曲 线和磁场为 零 时的能态密度曲 线 相 比 发生了巨大 变 化 , 形 成 了 一系列 的峰值 ,相邻 两 峰 之 间的能 量 差 是 。能 态 密度 变 化的这种 特 点 深刻 地影响了晶体的 物理性 质 。 D e Haas - V an A lphen效应 就是这 一 性质的 具 体反映 。 w c h N E( ) N E( ) 0 N E( ) B = 0 0 ( ) ( ) N E N E 见 方 俊鑫 书 6 .9 节 p 266

三、晶体中电子的有效质量近似 晶体中电子在磁场中运动时,其哈密顿量为 H=-(p+eA)'+U(r) 2m 其中,(为晶体的周期性势场,严格求解晶体中的电子 在磁场中的运动是非常困难的。但在有些情况下,可将哈 密顿量近似写成 H= 2m (p+eA) 这里,周期场的影响概括为有效质量的变化,称为有效质 量近似。一般半导体材料中,在导带底和价带顶附近常常 可以采用有效质量近似。对有些金属材料(如碱金属)有 时也可以采用。在有效质量近似的框架内,前面我们对自 由电子的讨论可以推广到晶体中的电子,只需用有效质量 m*代替自由电子的质量m即可
三、晶体中电子的有效质量近似 晶体中电子在磁场中运动时,其哈密顿量为 ( ) ( ) 1 2 2 H e U m = p + + A r 其中,U(r)为 晶体的周期性势场,严格求解晶体中的电子 在磁场中的运动是非常困难的。但在有些情况下,可将哈 密顿量近似写成 ( ) 1 2 2 H e m * = + p A 这里,周期场的影响概括为有效质量的变化,称为有效质 量近似。一般半导体材料中,在导带底和价带顶附近常常 可以采用有效质量近似。对有些金属材料(如碱金属)有 时也可以采用。在有效质量近似的框架内,前面我们对自 由电子的讨论可以推广到晶体中的电子,只需用有效质量 m* 代替自由电子的质量 m 即可
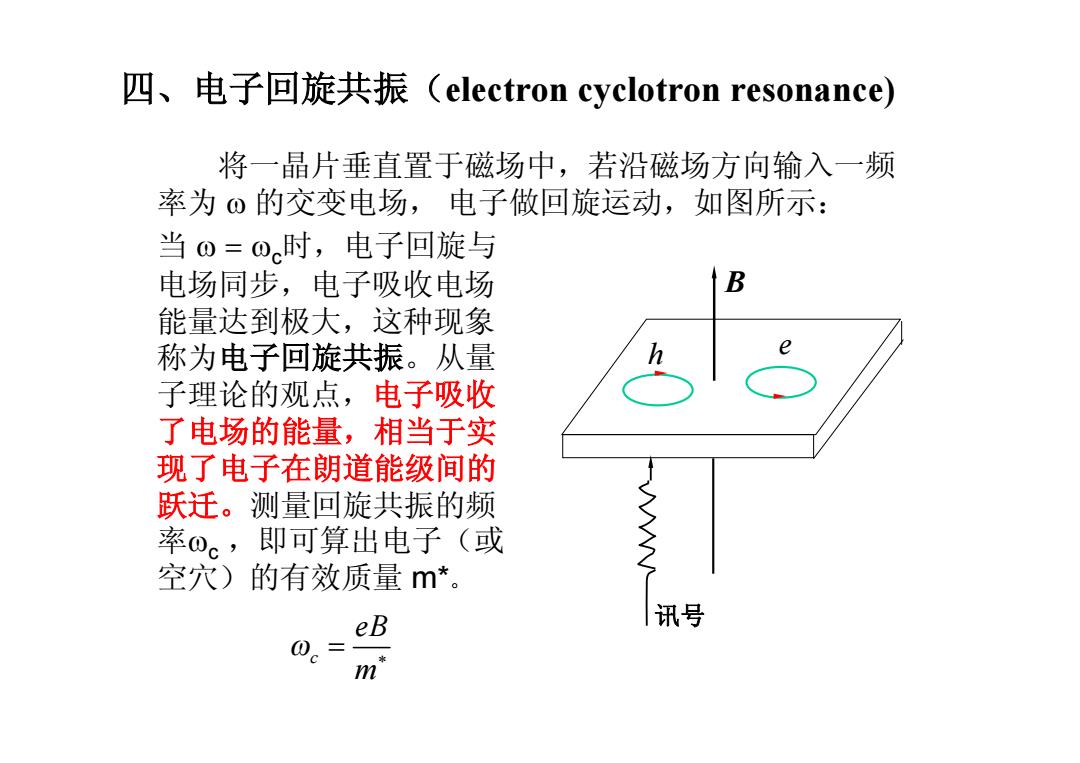
四、电子回旋共振(electron cyclotron resonance) 将一晶片垂直置于磁场中,若沿磁场方向输入一频 率为。的交变电场,电子做回旋运动,如图所示: 当0=0时,电子回旋与 电场同步,电子吸收电场 B 能量达到极大,这种现象 称为电子回旋共振。从量 子理论的观点,电子吸收 了电场的能量,相当于实 现了电子在朗道能级间的 跃迁。测量回旋共振的频 率o。,即可算出电子(或 空穴)的有效质量m*。 eB 讯号 0e m
四、电子回旋共振(electron cyclotron resonance) 将一晶片垂直置于磁场中,若沿磁场方向输入一频 率为 w 的交变电场, 电子做回旋运动,如图所示: 当 w = wc时,电子回旋与 电场同步,电子吸收电场 能量达到极大,这种现象 称为电子回旋共振。从量 子理论的观点,电子吸收 了电场的能量,相当于实 现了电子在朗道能级间的 跃迁。测量回旋共振的频 率wc ,即可算出电子(或 空穴)的有效质量 m*。 B e h 讯号 c eB m w * =