
对于自由电子: E- 一 (k)= m dk, eB dt m eB 有: m =0 或:v(k)= m 电子的运动轨道为圆,如下图 在等能线上,k,=const.. 2元=2πeB 2πeB eB T dk m.2元k, m hk
对于自由电子: ( ) = h 2 2 k E 2m k 电子的运动轨道为圆,如下图 ( ) ^ ^ = hk v m k 在等能线上,k^ = const. const 2 2 2 d 2 c E eB eB eB T m k m k v k p p w p p ^ = ^ ^ = = = = × ò v h h h Ñ d d d d d 0 d x y y x z k eB k t m k eB k t m k t = - = = ( ) ( ) d d k v k m k e k B t m = = - ´ r r h r r ur 有: 或:

磁场作用下自由电子 在k空间中的运动轨道 k常数 是圆。其回旋频率: eB 0。= m e常数 从前面讨论中可以看出: Bloch电子在磁场中虽然也在做回旋运动,但由于其等能面 的复杂变化(见6.8节),其运动轨迹要复杂的多,因而其 回旋频率的表达式需要具体积分求出。在能带底和能带顶, 情况变得简单,可以给出类似自由电子的表达式: eB 0e m*是Bloch电子的有效质量 m*
磁场作用下自由电子 在 k 空间中的运动轨道 是圆。其回旋频率: c eB m w = 从前面讨论中可以看出: Bloch 电子在磁场中虽然也在做回旋运动,但由于其等能面 的复杂变化(见 6.8 节),其运动轨迹要复杂的多,因而其 回旋频率的表达式需要具体积分求出。在能带底和能带顶, 情况变得简单,可以给出类似自由电子的表达式: * c eB m w = m* 是 Bloch 电子的有效质量
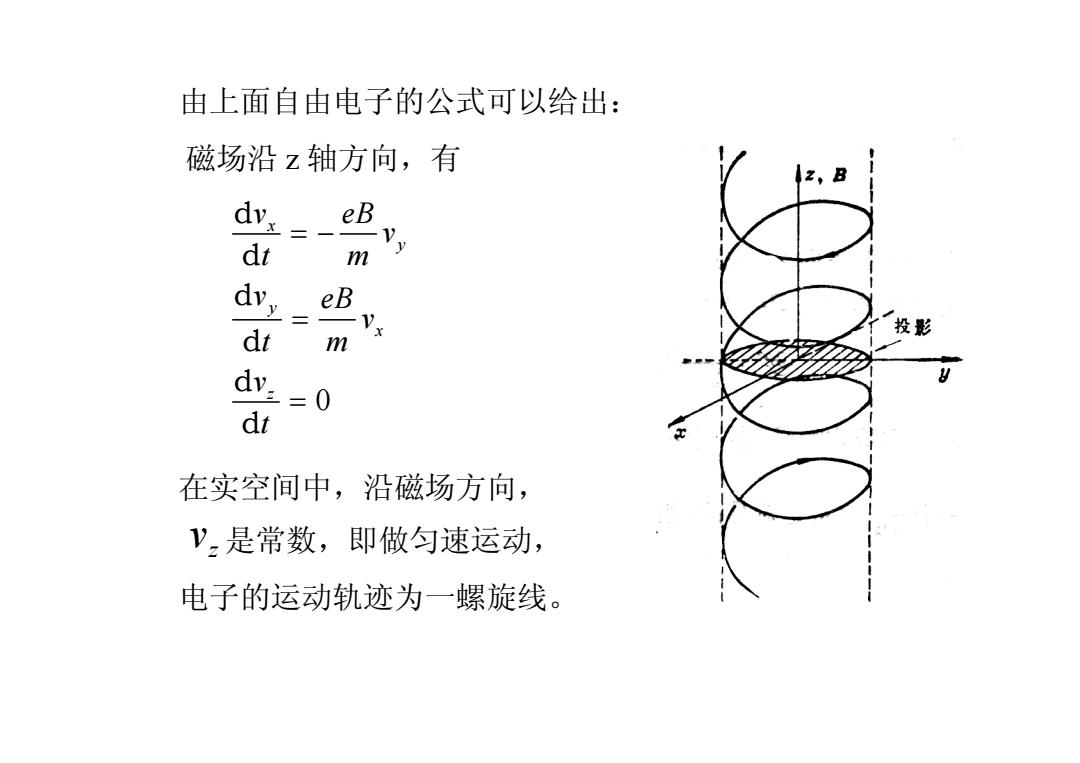
由上面自由电子的公式可以给出: 磁场沿z轴方向,有 dv:_ eB dt m dv. eB dt 投影 m =0 dt 在实空间中,沿磁场方向, V,是常数,即做匀速运动, 电子的运动轨迹为一螺旋线
在实空间中,沿磁场方向, 是常数,即做匀速运动, 电子的运动轨迹为一螺旋线。 由上面自由电子的公式可以给出: 磁场沿 z 轴方向,有 0 x y y x z v eB v t m v eB v t m v t = - = = d d d d d d z v

解为 Vx Vocos@t v +y2 Vy Vosin@ot eB v.const. 00 m 实空间中电子的运动图象:沿磁场方向(方向),电子作匀 速运动,在垂直于磁场的平面内,电子作匀速圆周运动。 eB 回转频率: 00= m 对于晶体中的电子 F=-evx B
解为 0 0 0 0 cos sin x y z v v v v v . w w = = = const t { t 2 2 2 0 0 x y v v v eB m w = + = 实空间中电子的运动图象:沿磁场方向(z方向),电子作匀 速运动,在垂直于磁场的平面内,电子作匀速圆周运动。 回转频率: 0 eB m w = 对于晶体中的电子 { d 1 dt m e * é ù = × ê ú ë û - ´ v F F = v B

在主轴坐标系中有 =1 v dv=. dt mx dt m. dt m. 若磁场方向取在z轴方向,B=B,即可写出其相 应的准经典运动方程。 dvs eB di mx dy. eB -V dt my dv. 0 dt 这与普通物理中的结果是一致的
在主轴坐标系中有 d 1 d 1 d 1 , , d d d x z y x y z x y z v v v F F F t m t m t m * * * === 若磁场方向取在 z轴方向,B=Bk,即可写出其相 应的准经典运动方程。 d d d d d 0 d x y x y x y z v eB v t m v eB v t m v t * * = - = = 这与普通物理中的结果是一致的