随着N的增加,ω减小,一旦N一>∞,上式就过液 为一个积分: Xieyehn X(ejkoeko -2m -T 0 图5.2(5.7)式的图解说明 X(eiw)对ω说是周期的,周期为2π;而ejw"对ω说 也是2π为周期的。所以乘积X(ejω)eiwn也一定是周 期的
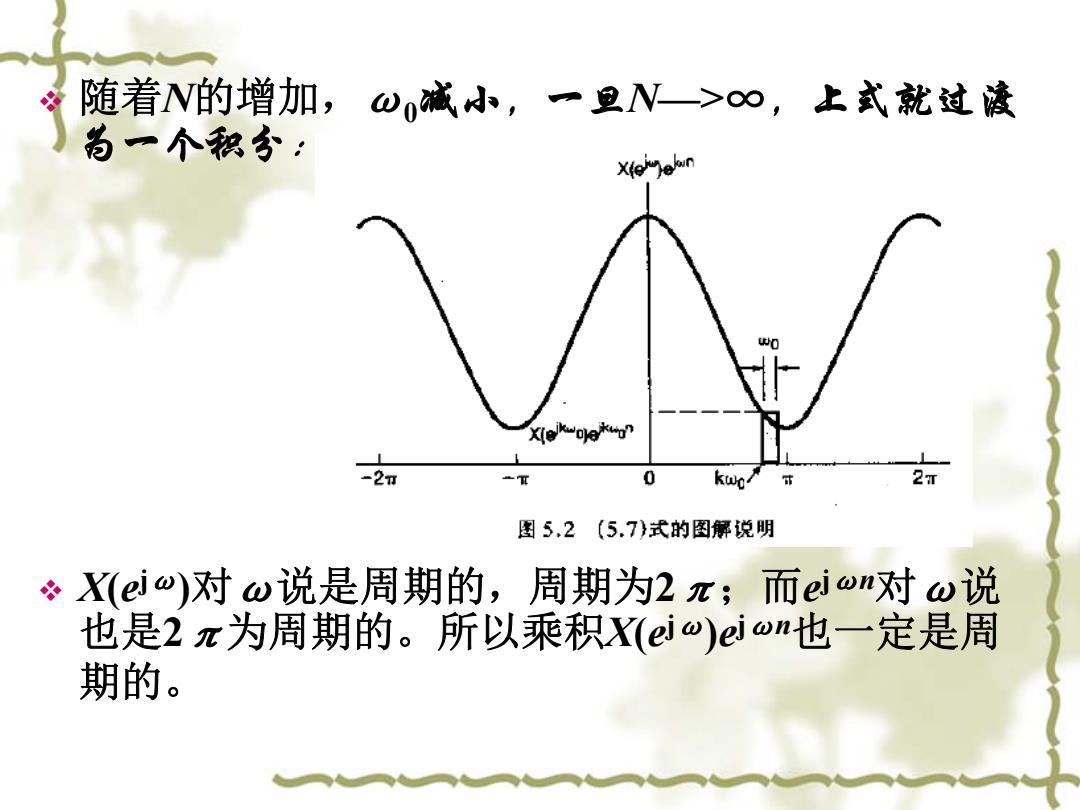
随着N的增加,ω0减小,一旦N—>∞,上式就过渡 为一个积分: X(ejω)对ω说是周期的,周期为2π;而ejωn对ω说 也是2π为周期的。所以乘积X(e jω)ejωn也一定是周 期的

因为这个求和是在N个宽为ω=2πN的矩形间隔内 完成的,所以总的积分区间总是有一个2π的宽 度,因此,随着N一>∞,有: tml-2zIXe9edo 十0∞ X(eo)=∑x[n]e n=-∞ 离散时间傅里叶变换对
因为这个求和是在N个宽为ω0 =2π/N的矩形间隔内 完成的,所以总的积分区间总是有一个2π的宽 度,因此,随着N—>∞,有: 离散时间傅里叶变换对。 2 1 [] ( ) 2 j jn x n Xe e d ω ω π ω π = ( ) [] j j n n X e xne ω ω +∞ − =−∞ =

。离散时间傅里叶变换与连续时间傅里叶变换之比较 两者的主要差别在于离散时间傅里叶变换X(io)的 周期性和在综合公式中的有限积分区间。而这两者 均来自这样一个事实:在频率上相差2π的离散时 间复指数信号是完全一样的
离散时间傅里叶变换与连续时间傅里叶变换之比较 两者的主要差别在于离散时间傅里叶变换X( ej ω ) 的 周期性和在综合公式中的有限积分区间。而这两者 均来自这样一个事实:在频率上相差 2 π的离散时 间复指数信号是完全一样的

(2)傅里叶变换(非周期信号) xIn]=%(n] -N,≤n≤W2 +N2 1 十0∞ n=-N1 ne=N∑fabe-xoxixw n=-00 如果定义:X(eJm)=∑x[n]ejam 那么: a) 周期序列=.石em心=证三Xee k=< 第5章离散时间傅里叶变换 14
第5章离散时间傅里叶变换 14 1 ≤≤− NnN 2 ][ ~ ][ = nxnx +∞ = −∞ − + −= − = = n nNjk N Nn nNjk k enx N enx N a )/2( )/2( ][ 1 ][ 1 2 1 π π nj n j eX enx ω − ω +∞ = −∞ 如果定义 = ][)( : 那么: )( 1 ω 0 jk k eX N a = 0 0 0 0 0 1 1 [] ( ) ( ) 2 jk jk n jk jk n k N k N xn X e e X e e N ω ω ω ω ω =< > π =< > 周期序列 = = (2)傅里叶变换(非周期信号)

当N∞, x[n”→xW 2π Nx∞→d0 N ko N-∞→0 网=m6-2元人eedn tml=2元.xee-do DTFT变换对 X(eo)=∑x[n]eJom x[n←r→X(e) N=-co 第5章离散时间傅里叶变换 15
第5章离散时间傅里叶变换 15 = = − ∞+ = −∞ nj N j njj eX enx nx deeX ω ω π ωω ω π ][)( )( 21 ][ 2 当 N→∞ , ω ω ω π ω ⎯⎯ →⎯ ⎯= ⎯ →⎯ ⎯⎯ →⎯ ∞→ ∞→ ∞→ N N N k d N nxnx 0 0 2 ][][~ = = ∞→ π ωω ω π 2 )( 21 ])[ ~(lim][ nxnx deeX njj N DTFT 变换对 ][ )( DTFT jω nx ←⎯ →⎯ eX