
5.1.2离散时间傅里叶变换举例 例5.1信号x[n=m"u[m,ld←1,求信号的频谱 X(em)=∑x[nle咖 n=-00 ∑a"une- = n=-0o 十0∞ ∑(ae)" n=0 1 1-ae-jo
5.1.2 离散时间傅里叶变换举例 例5.1 信号x[n]=anu[n], |a|<1,求信号的频谱 0 ( ) [] [ ] ( ) 1 1 j j n n n jn n j n n j X e xne aune ae ae ω ω ω ω ω +∞ − =−∞ +∞ − =−∞ +∞ − = − = = = = −
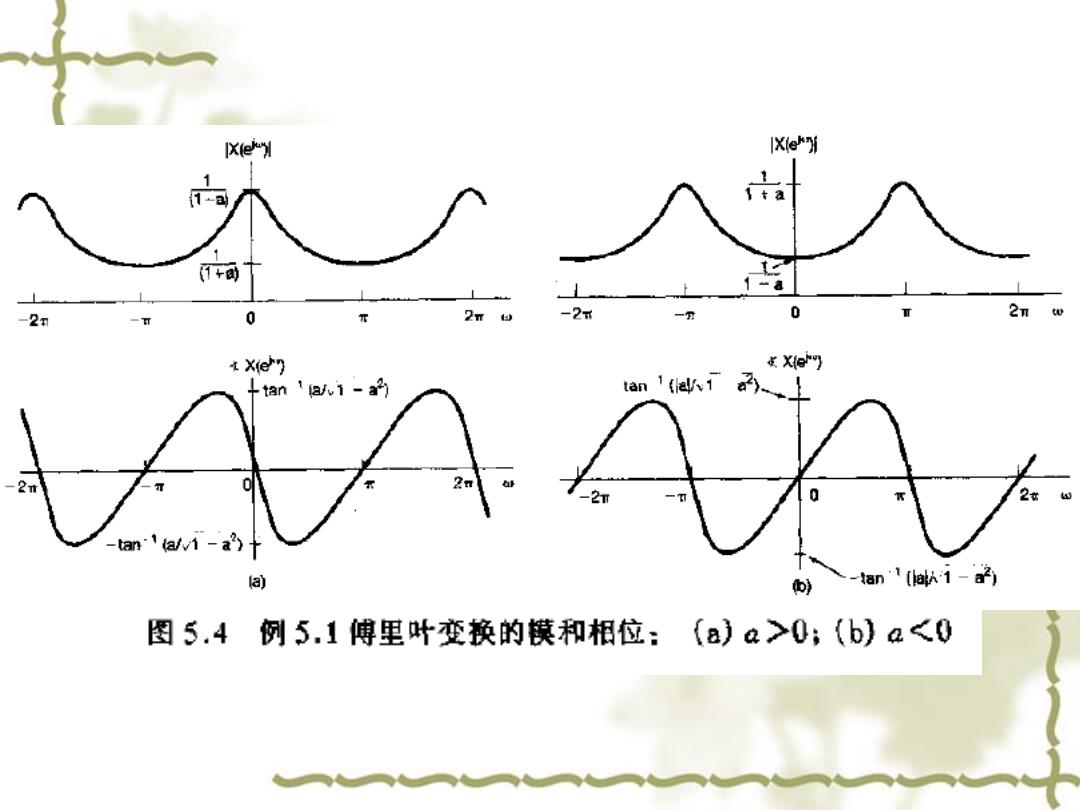
X(e") IX(e) 1 1 - it a T+西 -2知 0 -2m 2n -T iXe 发Xe +tan1aw1-a的 tan11上 -2t 2n -T -tan (a/wi-a)十 a o 入-an1e人1-子 图5.4例5.1傅里叶变换的模和相位:(a)a>0;(b)a<0
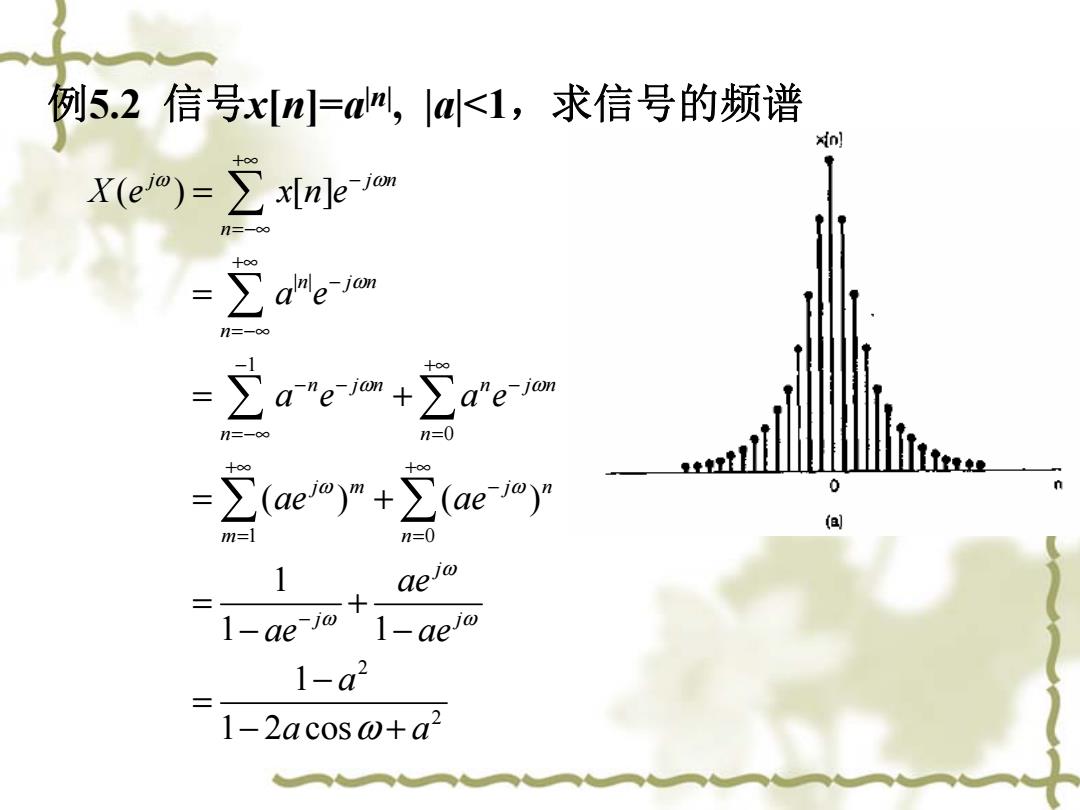
例5.2信号x[m=dm,|@<1,求信号的频谱 xin] X(eo)=∑x[nlen n=-c0 十 ∑aem n=-c0 aem+arem 十00 n=- n=0 =i(aey”+i(ae 0 (a m=] n=0 1 1-ae-io 1-aeio 1-a2 1-2acos @+a 2
例5.2 信号x[n]=a|n|, |a|<1,求信号的频谱 | | 1 0 1 0 2 ( ) [] ( ) ( ) 1 1 1 1 1 2 cos j j n n n jn n n jn n jn n n j m j n m n j j j X e xne a e a e ae ae ae ae ae ae a a a ω ω ω ω ω ω ω ω ω ω ω +∞ − =−∞ +∞ − =−∞ − +∞ − − − =−∞ = +∞ +∞ − = = − = = = + = + = + − − − = − + 2
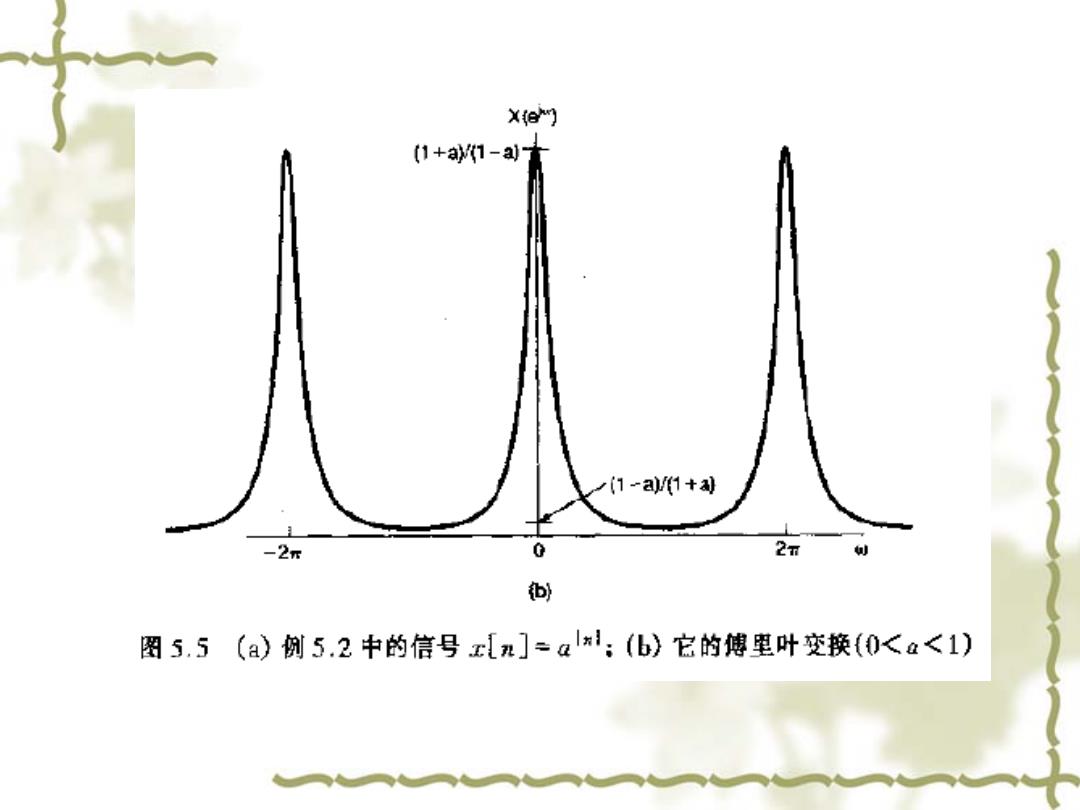
Xe们 (1+a1-a (1一a/1+ -2r 0 2T 创 图5,5(a)例5.2中的信号x[]-a:(b)它的傅里叶变换(0<a<1)
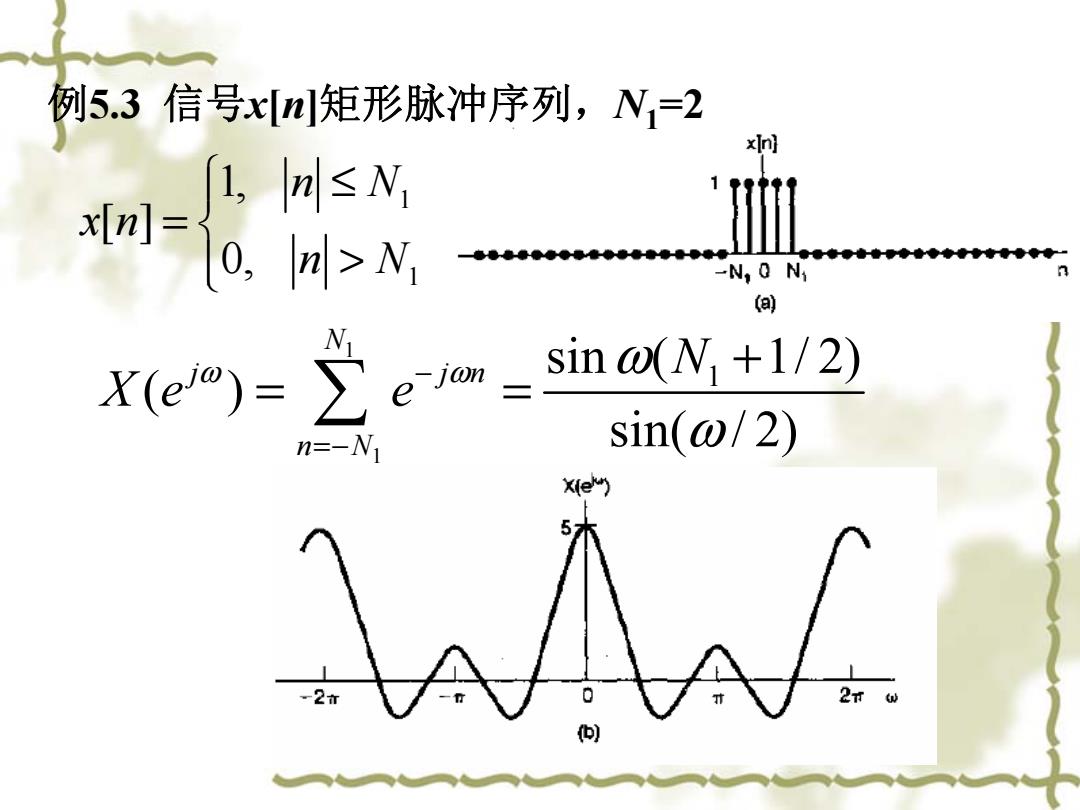
例5.3信号x[m矩形脉冲序列,N=2 x 1,lm≤N 刘m0,叫>N, -N,0N1 (a) xem=是e m= sin @(N +1/2) n=-N sin(@/2) X(e) -2 何)
例5.3 信号 x [ n ]矩形脉冲序列, N1 =2 1 1 1, [ ] 0, n N x n n N ≤ = > 1 1 1 sin ( 1/ 2) ( ) sin( / 2) N j jn n N N Xe e ω ω ω ω − =− + = =