
版权©2019,版权保留,侵犯必究 一阶非齐次常微分方程的求解 方程的解由非齐次方程的特解和对应的齐次方程的 通解两个分量组成: ()=(t)+心(t) 特解: (t)=1s 齐次方程 Ld(+i()=0 R dt 的通解:心(t)=Ae7 T= R 根据初始值,(0,)=1(0)=0,A=-1s i()=I(1-e).v(t)-Ldic()-RIe dt 复旦大学射频集成电路设计研究小组 0127- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0127- 一阶非齐次常微分方程的求解 方程的解由非齐次方程的特解和对应的齐次方程的 通解两个分量组成: 特解: 齐次方程 的通解: 根据初始值, ' '' L L L i t i t i t ( ) ( ) ( ) = + L L S i i A I (0 ) (0 ) 0, + − = = = − ' L S i t I ( ) = L L d ( ) ( ) 0 dt L i t i t R + = '' L ( ) e t τ i t A − = C L S L S d ( ) ( ) (1 e ), ( ) e d t t τ τ i t i t I v t L RI t − − = − = = L τ R =
版权©2019,版权保留,侵犯必究 电压和电流随时间变化的曲线 个 IsR Is 0 0 -Is 时间常数T=L/R 复旦大学射频集成电路设计研究小组 -0128- 唐长文
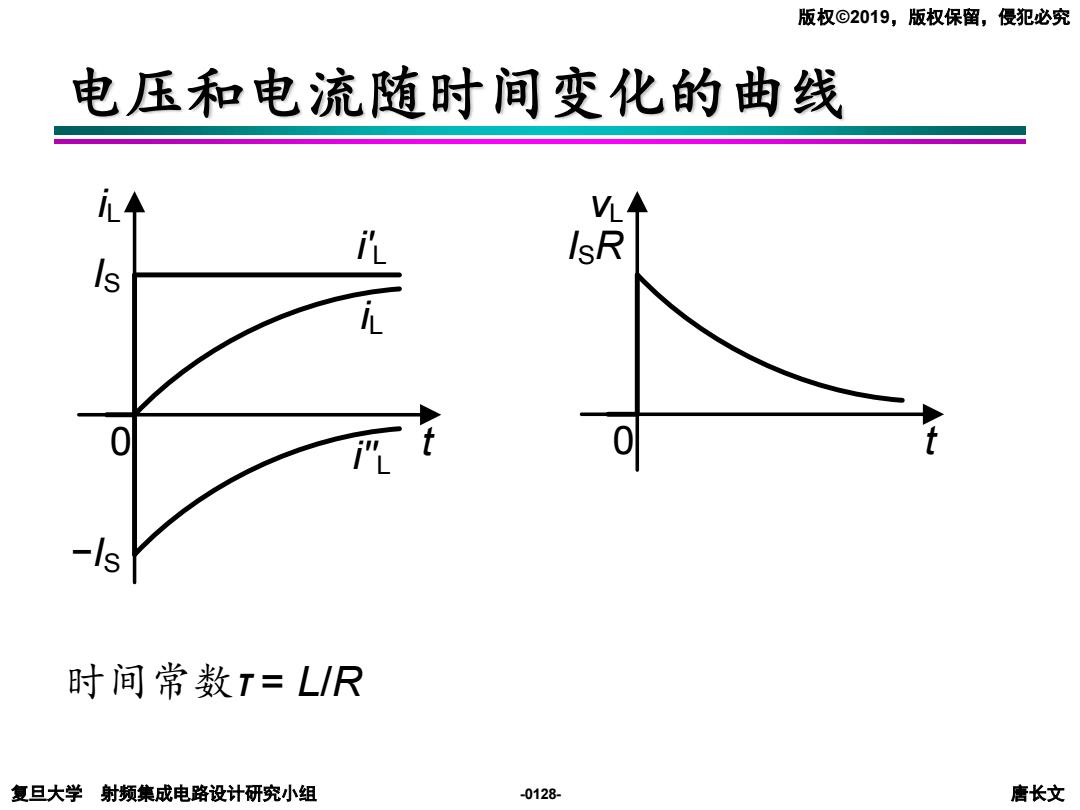
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0128- 电压和电流随时间变化的曲线 时间常数τ = L/R 0 iL IS t −IS iL i'L i''L 0 vL ISR t

版权©2019,版权保留,侵犯必究 正弦电源激励下RL电路零状态响应 Vs为正弦电压源 Vs Vsm cos(wt +o) 。 其中p0时接入相位角 Vs t≥0时,开关S接通, 电路的一阶常微分方程: VR(t)+Vc(t)=Vsm cos(wt+o), RCdvc(t)+Vc(t)-VsmCos(wt+) dt 初始值:Vc(0+)=Vc(0-)=0 复旦大学射频集成电路设计研究小组 0129- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0129- 正弦电源激励下RL电路零状态响应 vS为正弦电压源 其中φ0时接入相位角 t ≥ 0时,开关S接通, 电路的一阶常微分方程: 初始值: vC(0+ ) = vC(0− ) = 0 t=0 S vS R C iC vC S Sm 0 v V= + cos( ) ωt φ R C Sm 0 C C Sm 0 ( ) ( ) cos( ), d ( ) ( ) cos( ) dt v t v t V ωt φ v t RC v t V ωt φ + = + + = +

版权©2019,版权保留,侵犯必究 一阶非齐次常微分方程的求解 方程的解由非齐次方程的特解和对应的齐次方程的 通解两个分量组成: ve(t)=vc(t)+vc(t) 特解: vc(t)=Vcm cos(wt+) 正弦交流电路相量分析法 V.-必微c 1jwC 1 长1+jRC Vsm 1+(wRC)2 =Po-arctan(wRC) 复旦大学射频集成电路设计研究小组 -0130- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0130- 一阶非齐次常微分方程的求解 方程的解由非齐次方程的特解和对应的齐次方程的 通解两个分量组成: 特解: 正弦交流电路相量分析法 ' '' C C C v t v t v t ( ) ( ) ( ) = + ' C Cm i v t V ( ) cos( ) = + ωt φ C S S Sm Cm i 0 2 1 j 1 1 j 1 j , arctan( ) 1 ( ) ωC V V V R ωC ωRC V V φ φ ωRC ωRC = = + + = = − +

版权©2019,版权保留,侵犯必究 齐次方程RCdvc(⑨+.)=0的道解:)=Ae dt T=RC 根据初始值,Vc(0,)=Vc(0)=0 Vc(t)=Vcm Cos(wt+)+Ae 0 Vc(0.)=Vcm cos()+Ae "=0,A=-Vcm cos() vc(t)=Vcm cos(wt+)-Vcm cos()e (t >0) 复旦大学射频集成电路设计研究小组 -0131- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0131- 齐次方程 的通解: 根据初始值, C C v v (0 ) (0 ) 0 + − = = C C d ( ) ( ) 0 dt v t RC v t + = '' C ( ) e t τ v t A − = C Cm i 0 C Cm i Cm i C Cm i Cm i (t) cos( ) e (0 ) cos( ) e 0, cos( ) (t) cos( ) cos( )e , ( 0) tτ τ tτ v V ωt φ A v V φ A A V φ v V ωt φ V φ t − − + − = + + = + = = − = + − τ = RC