
版权©2019,版权保留,侵犯必究 第九章线性动态电路的复频域分析 。拉普拉斯变换及其基本性质 ·拉普拉斯逆变换 ·复频域中的电路定理和电路模型 ·拉普拉斯变换分析线性动态电路的暂 态过程 。复频域网络函数 复旦大学射频集成电路设计研究小组 -012- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -012- 第九章 线性动态电路的复频域分析 ⚫ 拉普拉斯变换及其基本性质 ⚫ 拉普拉斯逆变换 ⚫ 复频域中的电路定理和电路模型 ⚫ 拉普拉斯变换分析线性动态电路的暂 态过程 ⚫ 复频域网络函数

版权©2019,版权保留,侵犯必究 拉普拉斯变换和逆变换 拉普拉斯变换 F(s)=e(f(t))=f(t)e-*dt 其中复参量S=o+jw,也称复频率 拉普拉斯反变换 F(F()e"dt 原函数f)和象函数F(S) 复旦大学射频集成电路设计研究小组 -013- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -013- 拉普拉斯变换和逆变换 拉普拉斯变换 其中复参量s = σ + jω,也称复频率 拉普拉斯反变换 原函数f(t)和象函数F(s) 0 ( ) { ( )} ( )e d st F s f t f t t − − = = L j 1 j 1 ( ) { ( )} ( )e d 2πj σ st σ f t F s F s t + − − = = L

版权©2019,版权保留,侵犯必究 单位阶跃函数 ()()e"d- 100 1 二 s 单位冲激函数 F(s)=(t)=(t)edt=(t)edt=e-0-1 指数函数 00 F(s)-efe)eed- 1e(s-0)t 1 三 S+a 10 S+a 复旦大学射频集成电路设计研究小组 -014- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -014- 单位阶跃函数 单位冲激函数 指数函数 0 0 0 1 1 ( ) { ( )} ( )e d e d e st st st F s ε t ε t t t − + s s + − − − = = = = − = L 0 0 0 0 ( ) { ( )} ( )e d ( )e d e 1 st st s F s δ t δ t t δ t t + − − − − − = = = = = L ( ) 0 0 1 1 ( ) {e } e e d e αt αt st s α t F s t − s α s α − − − − − + = = = = + + L
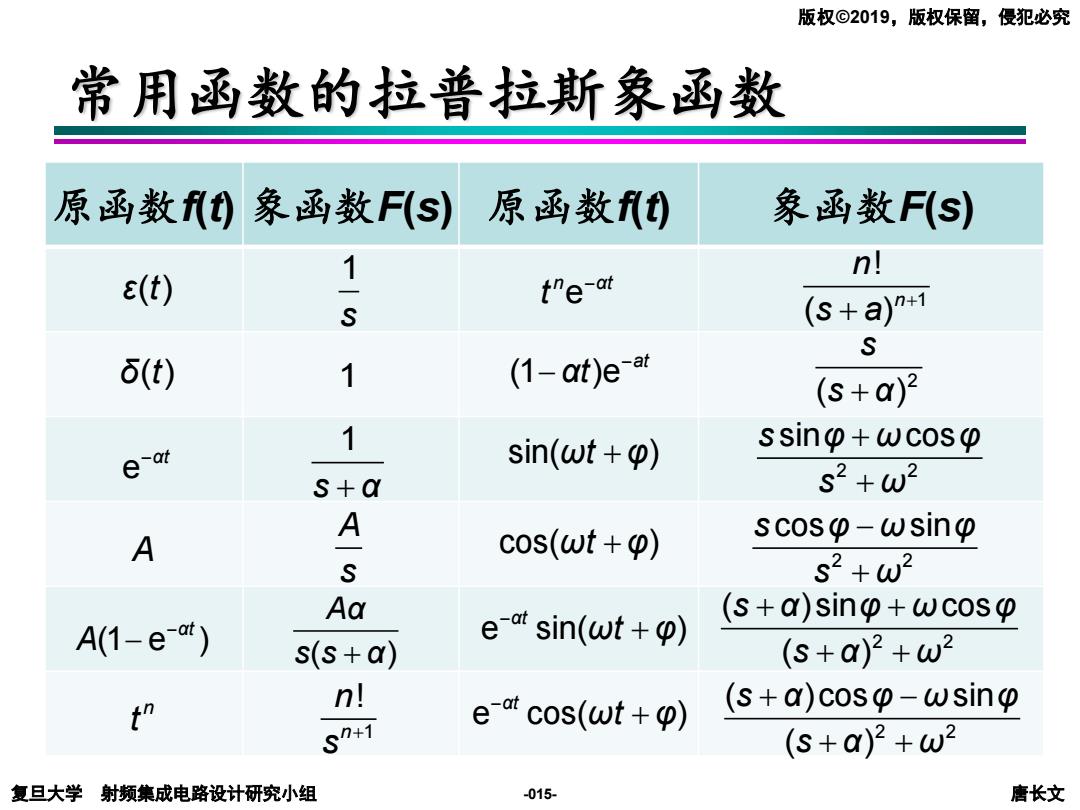
版权©2019,版权保留,侵犯必究 常用函数的拉普拉斯象函数 原函数f)象函数F(S) 原函数) 象函数F(S) a(t) 1 n! the-at (s+a)n*1 S δ(t) 1 (1-at)e-at (S+a)2 sin(wt + ssin+wcos e-at S+Q s2+w2 A scos-wsin A cos(wt + S s2+w2 Aa e-sin(wt + (s+a)sin+wcos A(1-e-t) s(S+a) (S+a)2+w2 n! (s+a)cos-wsin S47 e-cos(wt+p) (S+a)2+w2 复旦大学射频集成电路设计研究小组 -015- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -015- 常用函数的拉普拉斯象函数 原函数f(t) 象函数F(s) 原函数f(t) 象函数F(s) ε( )t 1 s δ( )t 1 2 2 ( )cos sin ( ) s α φ ω φ s α ω + − + + e cos( ) αt ωt φ − + e sin( ) αt ωt φ − + 2 2 ( )sin cos ( ) s α φ ω φ s α ω + + + + sin( ) ωt + φ cos( ) ωt + φ 2 2 s sin cos φ ω φ s ω + + 2 2 s cos sin φ ω φ s ω − + e n αt t − (1 )e at αt − − 1 ! ( )n n s a + + 2 ( ) s s + α (1 e ) αt A − − n t ( ) Aα s s + α 1 ! n n s + e −αt 1 s + α A A s

版权©2019,版权保留,侵犯必究 拉普拉斯变换的基本性质 线性叠加特性 elaf (t)+bf,(t))=aeif (t))+beif,(t)) 例题:1.求f)=A(1-e-a)的象函数F(S)。 F(s)=E{A(1-er)}=A(P{1-E{e-t}) Aa s(s+a) 2.求f)=sin(wt)的象函数F(s)。 F(s-e4shaw=e4(e-e} efcoswt)=sw S Γs2+w2 复旦大学射频集成电路设计研究小组 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -016- 拉普拉斯变换的基本性质 线性叠加特性 例题:1.求f(t) = A(1 − e −αt )的象函数F(s)。 2.求f(t) = sin(ωt)的象函数F(s)。 1 2 1 2 L L L { ( ) ( )} { ( )} { ( )} af t bf t a f t b f t + = + ( ) { (1 e )} ( {1} {e }) 1 1 ( ) ( ) αt αt F s A A Aα A s s α s s α − − = − = − = − = + + L L L j j 2 2 1 ( ) {sin } { (e e )} 2 j 1 1 1 ( ) 2j j j ωt ωt F s ωt ω s ω s ω s ω − = = − = − = − + + L L 2 2 {cos } s ωt s ω = + L