
《离散数学》课程教学大纲 DISCRETE MATHEMATICS 执笔者:任朝晖吴臣何志敏 审核人:胡小生 编写日期:2017年9月 一、课程基本信息 适用专业 网络工程 开课单位 电子信息工程学院 课程类型 专业基础课 课程性质 必修课 是否为双语 否 学分数 4学分 学时数 总学时64,其中:实验(实训)学时:课外学时 先修课程 线性代数 后续课程 数据结构、数据库系统原理 二、课程简述 离散数学课程是高等学校数学系和计算机系的一门必修的学科基础课程,其教学目 的是通过本课程的学习,使学生理解和掌握集合论、数理逻辑、代数系统、图论等方面 所阐述的基本理论、基本概念以及离散对象之间的数量结构和相互关系。 离散数学理论体系完整,结构严谨,具有广泛的应用实例。它是学习后继专业课程不可 缺少的数学工具。该课程结合计算机学科的特点,主要研究离散量结构及相互关系,是一门 理论性较强、应用性较广的课程。 离散数学对于计算机理论和实践是必不可少的工具性学科。通过对本课程的学习,使学 生能够接受现代数学关于离散结构的观点。从系统结构研究出发研究事物间的有关属性:同 时要应用数形结合方法,使事物论证简洁直观,并培养学生具有这种论证能力。同时通过描 述方法和缜密思维方法的训练,使学生具有良好的抽象思维和逻辑思维能力。 本课程的先修课程有《线性代数》、《数学分析》。 三、本课程所支撑的毕业要求 本课程支撑的毕业要求如下: 34
34 《离散数学》课程教学大纲 DISCRETE MATHEMATICS 执笔者:任朝晖 吴臣 何志敏 审核人:胡小生 编写日期:2017 年 9 月 一、课程基本信息 适用专业 网络工程 开课单位 电子信息工程学院 课程类型 专业基础课 课程性质 必修课 是否为双语 否 学分数 4 学分 学时数 总学时 64,其中:实验(实训)学时;课外学时 先修课程 线性代数 后续课程 数据结构、数据库系统原理 二、课程简述 离散数学课程是高等学校数学系和计算机系的一门必修的学科基础课程,其教学目 的是通过本课程的学习,使学生理解和掌握集合论、数理逻辑、代数系统、图论等方面 所阐述的基本理论、基本概念以及离散对象之间的数量结构和相互关系。 离散数学理论体系完整,结构严谨,具有广泛的应用实例。它是学习后继专业课程不可 缺少的数学工具。该课程结合计算机学科的特点,主要研究离散量结构及相互关系,是一门 理论性较强、应用性较广的课程。 离散数学对于计算机理论和实践是必不可少的工具性学科。通过对本课程的学习,使学 生能够接受现代数学关于离散结构的观点。从系统结构研究出发研究事物间的有关属性;同 时要应用数形结合方法,使事物论证简洁直观,并培养学生具有这种论证能力。同时通过描 述方法和缜密思维方法的训练,使学生具有良好的抽象思维和逻辑思维能力。 本课程的先修课程有《线性代数》、《数学分析》。 三、本课程所支撑的毕业要求 本课程支撑的毕业要求如下:
序号 毕业要求 课程内容对应的毕业要求指标点 毕业要求1工程知识学习能力:能够将 数学、自然科学知识以及相关的工程基 指标点1-1:具有解决网络工程相关问 1 础理论和专业知识用于解决网络工程 题所需的数学与自然科学知识及其应 中出现的一般技术与复杂工程等问题, 用能力。 并了解本专业发展现状和趋势。 毕业要求1-工程知识学习能力:能够 将数学、自然科学知识以及相关的工程 指标点1-4:能够运用数学、自然科学、 2 基础理论和专业知识用于解决网络工 工程基础理论和专业知识解决复杂网 程中出现的一般技术与复杂工程等问 络工程工程问题。 题,并了解本专业发展现状和趋势。 毕业要求2问题分析:能够应用数学、 自然科学和计算机网络的基本原理,通 指标点2-2:能够针对网络工程工程问 过文献研究,识别、表达、分析计算机 题选择正确、可用的数学模型。 网络工程问题,以获得有效结论。 毕业要求2-问题分析:能够应用数学、 指标点2-3:能够对于模型的正确性进 自然科学和计算机网络的基本原理,通 行论证并求解。 过文献研究,识别、表达、分析计算机 网络工程问题,以获得有效结论。 毕业要求3设计/开发解决方案能 力: 能够针对网络工程应用的特定需 求,设计适当的流程、方案,选取合适 指标点3-1:能够对网络工程专业复杂 的技术予以实现,并在设计或开发的过 工程问题进行分析,设计解决方案。 程中考虑社会、健康、安全、法律、文 化及环境因素。 毕业要求4(研究能力:基于科学原 理和网络工程应用构建的基本理论,对 指标点4-1:能够对计算机工程相关的 网络工程问题进行科学研究,包括流程 6 各类问题进行进行科学研究和实验验 设定、数据分析、结果论证、工程管理 证。 等,并通过信息综合得到合理有效的结 论。 35
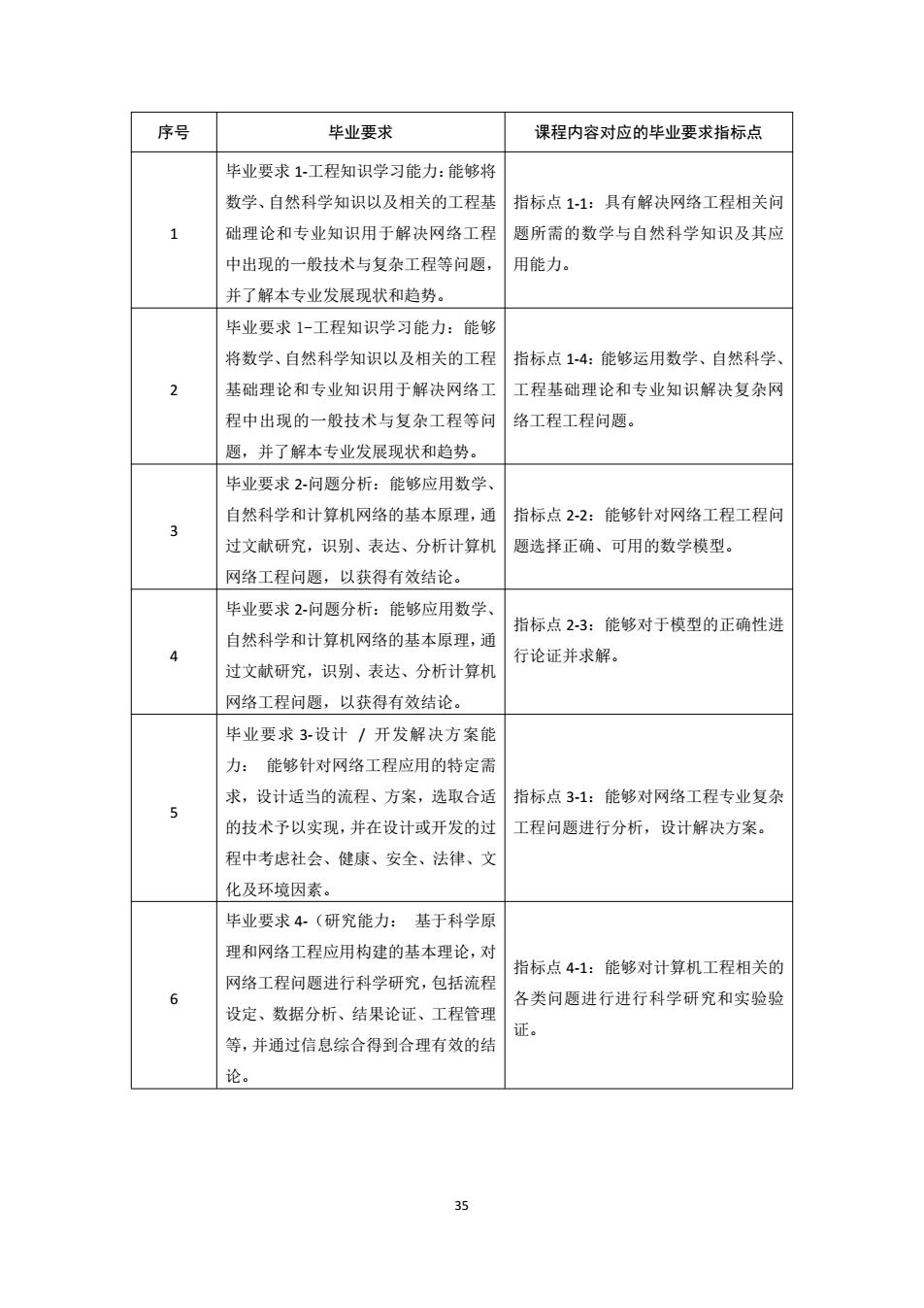
35 序号 毕业要求 课程内容对应的毕业要求指标点 1 毕业要求 1-工程知识学习能力:能够将 数学、自然科学知识以及相关的工程基 础理论和专业知识用于解决网络工程 中出现的一般技术与复杂工程等问题, 并了解本专业发展现状和趋势。 指标点 1-1:具有解决网络工程相关问 题所需的数学与自然科学知识及其应 用能力。 2 毕业要求 1-工程知识学习能力:能够 将数学、自然科学知识以及相关的工程 基础理论和专业知识用于解决网络工 程中出现的一般技术与复杂工程等问 题,并了解本专业发展现状和趋势。 指标点 1-4:能够运用数学、自然科学、 工程基础理论和专业知识解决复杂网 络工程工程问题。 3 毕业要求 2-问题分析:能够应用数学、 自然科学和计算机网络的基本原理,通 过文献研究,识别、表达、分析计算机 网络工程问题,以获得有效结论。 指标点 2-2:能够针对网络工程工程问 题选择正确、可用的数学模型。 4 毕业要求 2-问题分析:能够应用数学、 自然科学和计算机网络的基本原理,通 过文献研究,识别、表达、分析计算机 网络工程问题,以获得有效结论。 指标点 2-3:能够对于模型的正确性进 行论证并求解。 5 毕业要求 3-设计 / 开发解决方案能 力: 能够针对网络工程应用的特定需 求,设计适当的流程、方案,选取合适 的技术予以实现,并在设计或开发的过 程中考虑社会、健康、安全、法律、文 化及环境因素。 指标点 3-1:能够对网络工程专业复杂 工程问题进行分析,设计解决方案。 6 毕业要求 4-(研究能力: 基于科学原 理和网络工程应用构建的基本理论,对 网络工程问题进行科学研究,包括流程 设定、数据分析、结果论证、工程管理 等,并通过信息综合得到合理有效的结 论。 指标点 4-1:能够对计算机工程相关的 各类问题进行进行科学研究和实验验 证
(一)本课程内容与毕业要求指标点的对应关系 教学内容 毕业要求指标点 第一章命题逻辑基本概念 毕业要求1-1、1-4、2-3、3-1、4-1 第二章命题逻辑等值演算 毕业要求1-1、1-4、2-3、3-1、4-1 第三章命题逻辑的推理理论 毕业要求1-1、1-4、2-3、3-1、4-1 第四章一阶逻辑基本概念 毕业要求1-1、1-4、2-3、3-1、4-1 第五章一阶逻辑等值演算与推理 毕业要求1-1、1-4、2-3、3-1、4-1 理论教学 第六章集合代数 毕业要求1-1、1-4、2-2、3-1、4-1 第七章二元关系 毕业要求1-1、1-4、2-2、3-1、4-1 第八章函数 毕业要求1-1、1-4、2-2、3-1、4-1 第九章代数系统 毕业要求1-1、1-4、2-2、3-1、4-1 第十章半群与群 毕业要求1-1、1-4、2-2、3-1、4-1 第十四章图的基本概念 毕业要求1-1、1-4、2-2、3-1、4-1 第十六章树 毕业要求1-1、1-4、2-2、3-1、4-1 (二)毕业要求指标点在本课程中的实现路径 本课程通过设立若干课程目标来实现对毕业要求指标点的支撑。具体课程目标及其与毕 业要求指标点的主要对应关系如下: 课程目标1:培养数理逻辑部分训练逻辑推导能力 课程目标2:集合论、代数系统、图论让学生初步具有系统化、模型的概念并实际了解 图这个计算机中重要的数据结构的基本概念及用途 毕业要求指标点 课程教学目标 毕业要求1-1 课程目标1、2 毕业要求1-4 课程目标1、2 毕业要求2-2 课程目标1、2 毕业要求2-3 课程目标1、2 毕业要求3-1 课程目标1、2 毕业要求4-1 课程目标1、2 四、考核方式及成绩评定 (一)考核目标 数理逻辑、集合论、代数结构和图论等离散数学的基本概念和基本原理:抽象思维和逻 辑推理能力:应用数形结合方法对事物论证的能力:不同事物间相互关系和相互转化的能力: 对事物的描述方法和缜密思维方法掌握程度。 (二)考核方式 闭卷考试。 36
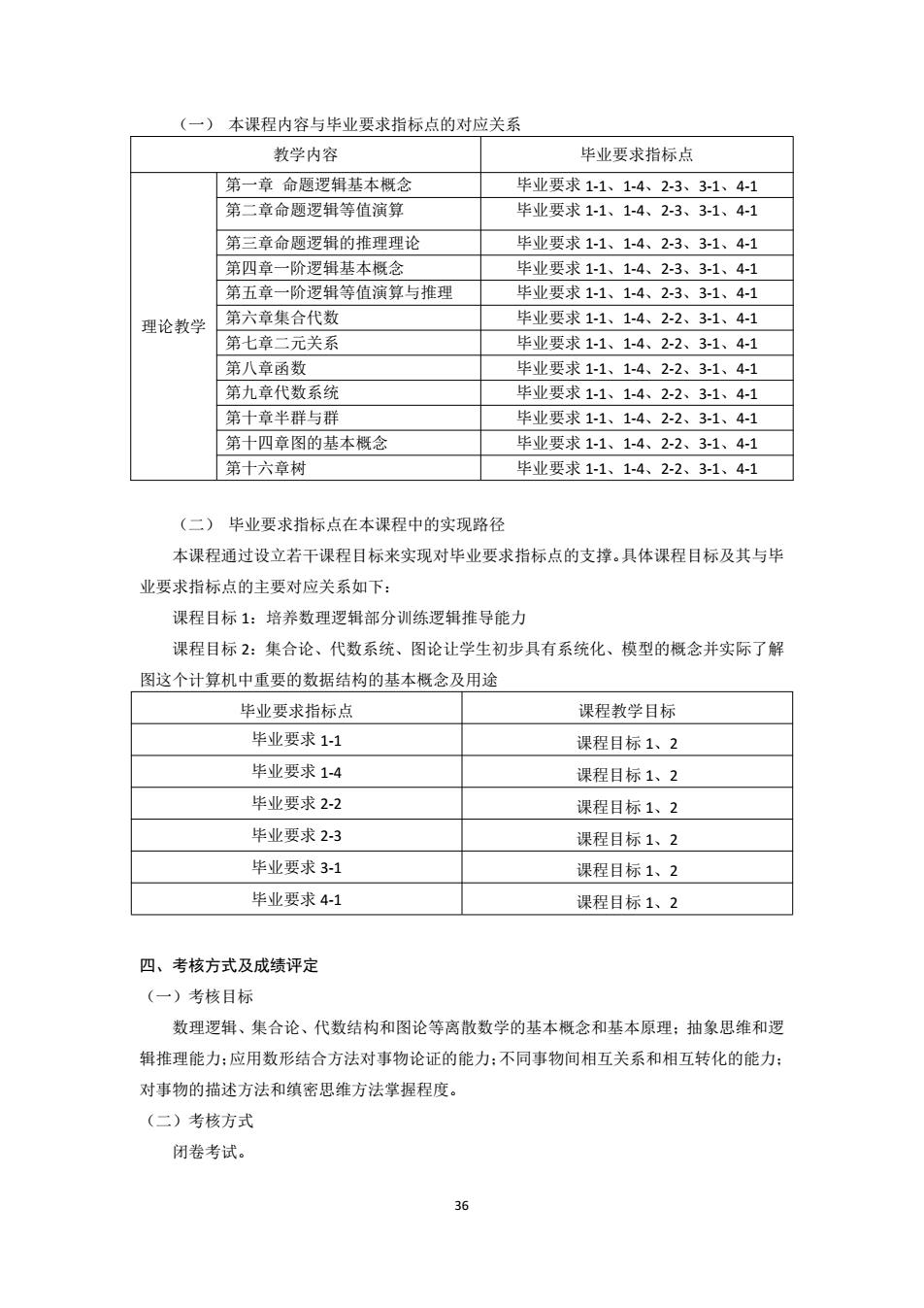
36 (一) 本课程内容与毕业要求指标点的对应关系 教学内容 毕业要求指标点 理论教学 第一章 命题逻辑基本概念 毕业要求 1-1、1-4、2-3、3-1、4-1 第二章命题逻辑等值演算 毕业要求 1-1、1-4、2-3、3-1、4-1 第三章命题逻辑的推理理论 毕业要求 1-1、1-4、2-3、3-1、4-1 第四章一阶逻辑基本概念 毕业要求 1-1、1-4、2-3、3-1、4-1 第五章一阶逻辑等值演算与推理 毕业要求 1-1、1-4、2-3、3-1、4-1 第六章集合代数 毕业要求 1-1、1-4、2-2、3-1、4-1 第七章二元关系 毕业要求 1-1、1-4、2-2、3-1、4-1 第八章函数 毕业要求 1-1、1-4、2-2、3-1、4-1 第九章代数系统 毕业要求 1-1、1-4、2-2、3-1、4-1 第十章半群与群 毕业要求 1-1、1-4、2-2、3-1、4-1 第十四章图的基本概念 毕业要求 1-1、1-4、2-2、3-1、4-1 第十六章树 毕业要求 1-1、1-4、2-2、3-1、4-1 (二) 毕业要求指标点在本课程中的实现路径 本课程通过设立若干课程目标来实现对毕业要求指标点的支撑。具体课程目标及其与毕 业要求指标点的主要对应关系如下: 课程目标 1:培养数理逻辑部分训练逻辑推导能力 课程目标 2:集合论、代数系统、图论让学生初步具有系统化、模型的概念并实际了解 图这个计算机中重要的数据结构的基本概念及用途 毕业要求指标点 课程教学目标 毕业要求 1-1 课程目标 1、2 毕业要求 1-4 课程目标 1、2 毕业要求 2-2 课程目标 1、2 毕业要求 2-3 课程目标 1、2 毕业要求 3-1 课程目标 1、2 毕业要求 4-1 课程目标 1、2 四、考核方式及成绩评定 (一)考核目标 数理逻辑、集合论、代数结构和图论等离散数学的基本概念和基本原理;抽象思维和逻 辑推理能力;应用数形结合方法对事物论证的能力;不同事物间相互关系和相互转化的能力; 对事物的描述方法和缜密思维方法掌握程度。 (二)考核方式 闭卷考试

(三)成绩评定 总评成绩包括期末考试(占70%)、平时考勤和作业(占30%,其中考勤占10%,作业 占20%)。 五、课程内容、重点和难点及教学方法与手段 第1章命题逻辑基本概念 重点:条件式、相容或与排斥或、重言式和矛盾式、真值表 难点:条件式 教学方法与手段:课堂多媒体教学+作业+课外学习 第1.1节 命题和联结词 了解简单命题、复合命题:深刻理解五种常用联结词的涵义。 第1.2节 命题公司及其赋值 深刻理解命题公式的赋值、成真赋值、成假赋值、重言式、矛盾式、可满足式:熟练写 出命题公式的真值表。 基本要求:了解简单命题、复合命题,熟练使用真值表,深刻理解五种常用联结词的涵 义、重言式、矛盾式。 第2章命题逻辑等值演算 重点:基本等值式、等值演算、主范式(析取和合取) 难点:主范式 教学方法与手段:课堂多媒体教学+作业+学生课外学习。 第2.1节 等值式 深刻理解等值式的定义,了解公式之间的等值关系具有自反性、对称性、传递性:熟练 应用基本等值式及置换规则进行等值演算:掌握重言式和矛盾式的判别方法。 第2.2节 析取范式和合取范式 了解文字、简单析取式、简单合取式、析取范式、合取范式:深刻理解极小项、极大项 的定义,名称、下角标与成真赋值的关系,主析取范式与主合取范式:熟练掌握求主范式(析 取和合取)的方法:会用主析取范式求公式的成真赋值、成假赋值、判断公式的类型、判断 俩个公式是否等值。 第2.3节 联结词的完备集(可选) 了解真值函数和联结词完备集:了解将命题公式等值地化成某种联结词完备集中的公式 的方法。 第2.4节 可满足性问题与消解法(课外学习) 基本要求:了解等值式、文字、简单析取式、简单合取式、析取范式、合取范式,牢记 基本等值式,深刻理解极小项、极大项的定义,名称、下角标与成真赋值的关系,主析取范 式与主合取范式,熟练掌握求主范式(析取和合取)的方法。 37
37 (三)成绩评定 总评成绩包括期末考试(占 70%)、平时考勤和作业(占 30%,其中考勤占 10%,作业 占 20%)。 五、课程内容、重点和难点及教学方法与手段 第 1 章命题逻辑基本概念 第 1.1 节 命题和联结词 了解简单命题、复合命题;深刻理解五种常用联结词的涵义。 第 1.2 节 命题公司及其赋值 深刻理解命题公式的赋值、成真赋值、成假赋值、重言式、矛盾式、可满足式;熟练写 出命题公式的真值表。 基本要求:了解简单命题、复合命题,熟练使用真值表,深刻理解五种常用联结词的涵 义、重言式、矛盾式。 第 2 章命题逻辑等值演算 第 2.1 节 等值式 深刻理解等值式的定义,了解公式之间的等值关系具有自反性、对称性、传递性;熟练 应用基本等值式及置换规则进行等值演算;掌握重言式和矛盾式的判别方法。 第 2.2 节 析取范式和合取范式 了解文字、简单析取式、简单合取式、析取范式、合取范式;深刻理解极小项、极大项 的定义,名称、下角标与成真赋值的关系,主析取范式与主合取范式;熟练掌握求主范式(析 取和合取)的方法;会用主析取范式求公式的成真赋值、成假赋值、判断公式的类型、判断 俩个公式是否等值。 第 2.3 节 联结词的完备集(可选) 了解真值函数和联结词完备集;了解将命题公式等值地化成某种联结词完备集中的公式 的方法。 第 2.4 节 可满足性问题与消解法(课外学习) 基本要求:了解等值式、文字、简单析取式、简单合取式、析取范式、合取范式,牢记 基本等值式,深刻理解极小项、极大项的定义,名称、下角标与成真赋值的关系,主析取范 式与主合取范式,熟练掌握求主范式(析取和合取)的方法。 重点:条件式、相容或与排斥或、重言式和矛盾式、真值表 难点:条件式 教学方法与手段:课堂多媒体教学+作业+课外学习 重点:基本等值式、等值演算、主范式(析取和合取) 难点:主范式 教学方法与手段:课堂多媒体教学+作业+学生课外学习

第3章命题逻辑的推理理论 重点:基本蕴含式、P系统中构造证明的方法(即形式演绎法) 难点:命题符号化、形式演绎法 教学方法与手段:课堂多媒体教学+作业+学生课外学习。 第3.1节 推理的形式结构 了解蕴含式(条件重言式),牢记基本蕴含式,了解公式之间的等值关系具有自反性、反 对称性、传递性:了解推理的形式结构、判断推理(即蕴含式)正确的真值表法、等值演算 法、主析取范式法。 第3.2节自然推理系统P 牢记P(前提引入)规则、T(结论引入)规则、置换规则、推理规则(即基本蕴含式): 熟练掌握P系统中构造证明(形式演绎)的直接证明法、附加前提证明法、归谬法:熟练掌 握命题符号化的方法。 第3.3节 消解证明法(课外学习) 基本要求:了解蕴含式、自然推理系统P,牢记基本蕴含式,熟练掌握命题符号化的方法、 形式演绎法。 第4章一阶逻辑基本概念 重点:一阶逻辑符号化(即谓词逻辑符号化) 难点:谓词逻辑符号化 教学方法与手段:课堂多媒体教学+作业+学生课外学习。 第4.1节 一阶逻辑命题符号化 了解个体、谓词、量词、特性谓词的基本概念:熟练掌握给定命题符号化的方法,深刻 理解特性谓词和量词的搭配方式。 第4.2节 一阶逻辑公式及解释 了解永真式、矛盾式、可满足式的概念及判别方法:了解对于给定的解释判断给定公式 是否是命题,是真命题还是假命题的方法。 基本要求:了解一阶逻辑公式及解释,熟练掌握谓词逻辑的命题符号化的方法。 第5章一阶逻辑等值演算和推理 重点:谓词逻辑基本等值式、蕴含式、等值演算、US(-)、UG(V+)、ES(3-)、EG(3+) 规则、形式证明。 难点:形式证明、前束范式。 教学方法与手段:课堂多媒体教学+作业+学生课外学习。 第5.1节 一阶逻辑等值式与置换规则 深刻理解并牢记一阶逻辑(即谓词逻辑)中的重要等值式并熟练应用:熟练使用置换规 则、换名规则、代替规则 第5.2节 一阶逻辑前束范式(可选) 38
38 第 3 章命题逻辑的推理理论 第 3.1 节 推理的形式结构 了解蕴含式(条件重言式),牢记基本蕴含式,了解公式之间的等值关系具有自反性、反 对称性、传递性;了解推理的形式结构、判断推理(即蕴含式)正确的真值表法、等值演算 法、主析取范式法。 第 3.2 节 自然推理系统 P 牢记 P(前提引入)规则、T(结论引入)规则、置换规则、推理规则(即基本蕴含式); 熟练掌握 P 系统中构造证明(形式演绎)的直接证明法、附加前提证明法、归谬法;熟练掌 握命题符号化的方法。 第 3.3 节 消解证明法(课外学习) 基本要求:了解蕴含式、自然推理系统 P,牢记基本蕴含式,熟练掌握命题符号化的方法、 形式演绎法。 第 4 章一阶逻辑基本概念 第 4.1 节 一阶逻辑命题符号化 了解个体、谓词、量词、特性谓词的基本概念;熟练掌握给定命题符号化的方法,深刻 理解特性谓词和量词的搭配方式。 第 4.2 节 一阶逻辑公式及解释 了解永真式、矛盾式、可满足式的概念及判别方法;了解对于给定的解释判断给定公式 是否是命题,是真命题还是假命题的方法。 基本要求:了解一阶逻辑公式及解释,熟练掌握谓词逻辑的命题符号化的方法。 第 5 章一阶逻辑等值演算和推理 第 5.1 节 一阶逻辑等值式与置换规则 深刻理解并牢记一阶逻辑(即谓词逻辑)中的重要等值式并熟练应用;熟练使用置换规 则、换名规则、代替规则 第 5.2 节 一阶逻辑前束范式(可选) 重点:基本蕴含式、P 系统中构造证明的方法(即形式演绎法) 难点:命题符号化、形式演绎法 教学方法与手段:课堂多媒体教学+作业+学生课外学习。 重点:一阶逻辑符号化(即谓词逻辑符号化) 难点:谓词逻辑符号化 教学方法与手段:课堂多媒体教学+作业+学生课外学习。 重点:谓词逻辑基本等值式、蕴含式、等值演算、US(-)、UG(+)、ES(-)、EG(+) 规则、形式证明。 难点:形式证明、前束范式。 教学方法与手段:课堂多媒体教学+作业+学生课外学习